统计学——几种常见的假设检验
1、什么是假设检验?
假设检验(hypothesis testing),又称统计假设检验,是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。显著性检验是假设检验中最常用的一种方法,也是一种最基本的统计推断形式,其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断。常用的假设检验方法有Z检验、t检验、卡方检验、F检验等。
假设检验的步骤
①确定要进行检验的假设,包括原假设 H 0 H_0 H0和备择假设 H 1 H_1 H1
②选择检验的方法,计算统计量
③根据显著性水平,确定用于做出决策的拒绝域
④查看样本结果是否位于拒绝域内
⑤做出决策
假设检验的几个重要概念
- H 0 H_0 H0(原假设):即要对其进行检验的断言,除非有足够的证据拒绝,否则将接受原假设
- H 1 H_1 H1(备择假设):在拒绝原假设之后将要接受的断言,通常与原假设对立
- α \alpha α(显著性水平):指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值,必须在每一次统计检验之前确定,通常取 α \alpha α=0.05或 α \alpha α=0.01
- 单尾检验:拒绝域落在可能的数据集的一侧
- 双尾检验:拒绝域落在可能的数据集的两侧
使用单尾检验还是双尾检验取决于备择假设的形式:
| 拒绝域的位置 | 原假设 | 备择假设 |
|---|---|---|
| 双尾 | H 0 : θ = θ 0 H_0:\theta=\theta_0 H0:θ=θ0 | H 1 : θ ≠ θ 0 H_1:\theta\neq\theta_0 H1:θ=θ0 |
| 左单尾 | H 0 : θ ≥ θ 0 H_0:\theta\geq\theta_0 H0:θ≥θ0 | H 1 : θ < θ 0 H_1:\theta\ < \theta_0 H1:θ <θ0 |
| 右单尾 | H 0 : θ ≤ θ 0 H_0:\theta\leq\theta_0 H0:θ≤θ0 | H 1 : θ > θ 0 H_1:\theta\ > \theta_0 H1:θ >θ0 |
假设检验的基本思想
小概率原理:小概率事件在一次试验中是几乎不可能发生的,假若在一次试验中事件事实上发生了,那只能认为事件不是来自我们假设的总体,也就是认为我们对总体所做的假设不正确。
假设检验中的两类错误
①第一类错误(弃真错误):原假设事实上正确,可是检验统计量的观察值却落入拒绝域,因而否定了本来正确的假设, p ( 弃 真 ) = α p(弃真)=\alpha p(弃真)=α
②第二类错误(取伪错误):原假设事实上不正确,可是检验统计量的观察值却落入了接受域,因而没有否定本来不正确的原假设。
P值
当原假设为真时所得到的样本观察结果或更极端结果出现的概率。
如果P值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,我们拒绝原假设的理由越充分。
| P值 | 碰巧的概率 | 对原假设 H 0 H_0 H0 | 统计学意义 |
|---|---|---|---|
| p > 0.05 p>0.05 p>0.05 | 碰巧出现的可能性大于5% | 不能否定原假设 H 0 H_0 H0 | 两组差别无显著意义 |
| p < 0.05 p<0.05 p<0.05 | 碰巧出现的可能性小于5% | 可以否定原假设 H 0 H_0 H0 | 两组差别有显著意义 |
| p < 0.01 p<0.01 p<0.01 | 碰巧出现的可能性小于1% | 可以否定原假设 H 0 H_0 H0 | 两组差别有非常显著意义 |
2、卡方检验
卡方检验的根本思想在于比较理论频数和实际频数的吻合程度或拟合优度问题。卡方检验分为卡方拟合度检验和卡方独立性检验。
卡方分布:若n个相互独立的随机变量ξ₁,ξ₂,…,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布
卡方检验的思想:卡方检验是以 χ 2 \chi^2 χ2分布为基础的一种常用假设检验方法。
原假设 H 0 H_0 H0是:观察频数与期望频数没有差别。
χ 2 = ∑ ( A − E ) 2 E = ∑ i = 1 k ( A i − E i ) 2 E i \chi^2=\sum\frac{(A-E)^2}{E}=\displaystyle\sum_{i=1}^k\frac{(A_i-E_i)^2}{E_i} χ2=∑E(A−E)2=i=1∑kEi(Ai−Ei)2
A A A:某个类别的观察频数
E E E:基于 H 0 H_0 H0原假设计算出的期望频数
A − E A-E A−E:残差
求和之前除以期望频数的原因:观察频数与期望频数的差距是相对较大还是较小,取决于期望频数的大小。例如期望频数为1000,观察频数为1040和期望频数为10,观察频数为50,差值均为40,但是显然后者的期望与实际的差距显然大于前者的期望和实际的差距。
χ 2 \chi^2 χ2是观察频数与期望频数之间距离的一种度量指标,也是假设成立与否的度量指标。如果 χ 2 \chi^2 χ2值小,就倾向于不拒绝 H 0 H_0 H0;如果 χ 2 \chi^2 χ2值大,就倾向于拒绝H0。至于 χ 2 \chi^2 χ2在每个具体研究中究竟要大到什么程度才能拒绝 H 0 H_0 H0,则要借助于卡方分布求出所对应的P值来确定。
卡方检验的用途
1、检验某个连续变量的分布是否与理论分布一致
2、检验某个分类变量各类的出现概率是否等于指定概率
3、检验某两个分类变量是否相互独立。如吸烟是否与呼吸道疾病有关
4、检验控制某种或某几种分类因素的作用以后,另两个分类变量是否相互独立
卡方拟合优度检验的自由度为 d f = k − 1 df=k-1 df=k−1,其中k代表分类变量数
卡方独立性检验的自由度为 d f = ( R − 1 ) ( C − 1 ) df=(R-1)(C-1) df=(R−1)(C−1),R代表行数,C代表列数
卡方检验实例
- 卡方拟合优度检验
投掷骰子的观察分布是否等于期望分布。
H 0 H_0 H0:观察分布等于期望分布
假设投掷骰子共120次,各点数实际出现次数为A,期望出现次数为E,结果如下表:
| 点数 | 期望频数 | 实际频数 |
|---|---|---|
| 1 | 20 | 18 |
| 2 | 20 | 19 |
| 3 | 20 | 23 |
| 4 | 20 | 20 |
| 5 | 20 | 16 |
| 6 | 20 | 24 |
卡方值 χ 2 = ∑ ( A − E ) 2 E = 2.3 \chi^2=\displaystyle\sum\frac{(A-E)^2}{E}=2.3 χ2=∑E(A−E)2=2.3
自由度为 d f = k − 1 = 5 df=k-1=5 df=k−1=5
选择显著性水平 α = 0.05 \alpha=0.05 α=0.05
根据自由度和显著性水平,得到卡方临界值为 11.0705 11.0705 11.0705
由于 2.3 < 11.0705 2.3<11.0705 2.3<11.0705,故接受原假设,认为观察分布等于期望分布
- 卡方独立性检验
喝牛奶与感冒是否相关
H 0 H_0 H0:喝牛奶与感冒不相关
观测情况如下表:
| 感冒人数 | 不感冒人数 | 合计 | 感冒率 | |
|---|---|---|---|---|
| 喝牛奶 | 43 | 96 | 139 | 30.94% |
| 不喝牛奶 | 28 | 84 | 112 | 25.00% |
| 合计 | 71 | 180 | 251 | 28.29% |
假设喝牛奶与感冒是独立不相关的,则期望情况如下表:
| 感冒人数 | 不感冒人数 | 合计 | |
|---|---|---|---|
| 喝牛奶 | 139*28.29%=39.3231 | 139*(1-28.29%)=99.6769 | 139 |
| 不喝牛奶 | 112*28.29%=31.6848 | 112*(1-28.29%)=80.3152 | 112 |
| 合计 | 71 | 180 | 251 |
卡方值 χ 2 = ∑ ( A − E ) 2 E = 1.10 \chi^2=\displaystyle\sum\frac{(A-E)^2}{E}=1.10 χ2=∑E(A−E)2=1.10
自由度为 d f = ( R − 1 ) ( C − 1 ) = 1 df=(R-1)(C-1)=1 df=(R−1)(C−1)=1
选择显著性水平 α = 0.05 \alpha=0.05 α=0.05
根据自由度和显著性水平,得到卡方临界值为 3.841459 3.841459 3.841459
由于 1.10 < 3.841459 1.10<3.841459 1.10<3.841459,故接受原假设,认为喝牛奶与感冒是独立不相关的
3、Z检验
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。当已知标准差时,验证一组数的均值是否与某一期望值相等时,用Z检验。
- 检验一个样本的平均值与一个已知总体的平均值是否存在显著差异,Z值计算公式如下:
z = X ˉ − μ 0 S / n z=\frac{\bar X-\mu_0}{S/\sqrt{n}} z=S/nXˉ−μ0
其中
X ˉ \bar X Xˉ:样本平均值
μ 0 \mu_0 μ0:总体均值
S S S:总体标准差。当总体标准差未知且样本容量大时,取样本标准差
n n n:样本容量 - 检验来自两个不同总体的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显著,Z值计算公式:
z = X ˉ 1 − X ˉ 2 S 1 2 n 1 + S 2 2 n 2 z=\frac{\bar X_1-\bar X_2}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} z=n1S12+n2S22Xˉ1−Xˉ2
其中
X 1 X_1 X1:样本1的均值
X 2 X_2 X2:样本2的均值
S 1 S_1 S1:样本1的标准差
S 2 S_2 S2:样本2的标准差
n 1 n_1 n1:样本1的样本容量
n 2 n_2 n2:样本2的样本容量
Z检验的步骤
①确立原假设 H 0 H_0 H0:两个平均数之间没有差异
②根据z值计算公式计算出z值
③根据显著性关系与z值做出判断
| z值 | p值 | 差异程度 |
|---|---|---|
| ≥ \geq ≥ 2.58 | ≤ \leq ≤ 0.01 | 非常显著 |
| ≥ \geq ≥ 1.96 | ≤ \leq ≤ 0.05 | 显著 |
| <1.96 | >0.05 | 不显著 |
Z检验实例
根据过去大量资料,某厂生产的灯泡使用寿命符合正态分布N~ ( 1020 , 10 0 2 ) (1020,100^2) (1020,1002),从最近生产的一批灯泡中随机抽取100只,测得样本平均值为1080,在0.05的显著性水平下判断这批产品的使用使用寿命是否显著提高。
H 0 H_0 H0:样本均值与总体均值无显著差异
根据公式计算Z值为 z = X ˉ − μ 0 S / n = 1080 − 1020 100 / 100 = 6 z=\frac{\bar X-\mu_0}{S/\sqrt{n}}=\frac{1080-1020}{100/\sqrt{100}}=6 z=S/nXˉ−μ0=100/1001080−1020=6
在0.05的显著性水平下,由于8>1.96,因此拒绝原假设,认为样本均值与总体均值存在显著差异。
4、T检验
T检验是用于小样本(样本容量小于30)的两个平均值差异程度的检验方法。T检验是通过比较不同数据的均值,研究两组数据之间是否存在显著差异。
T检验的适用条件为样本分布符合正态分布。
T检验的应用条件:
当样本例数较小时,要求样本取自正态总体
做两样本均数比较时,还要求两样本的总体方差相等。
T检验的用途:
(1)样本均数与群体均数的比较
(2)两样本均数的比较
-
单个样本的t检验
用于检验样本的分布期望是否等于某个值,原假设: μ = μ 0 \mu=\mu_0 μ=μ0
统计量计算:
t = X ˉ − μ 0 S / n t=\frac{\bar X-\mu_0}{S/\sqrt{n}} t=S/nXˉ−μ0
自由度 v = n − 1 v=n-1 v=n−1
适用条件:
(1) 已知一个总体均数 μ 0 \mu_0 μ0;
(2) 可得到一个样本均数 X ˉ \bar X Xˉ及该样本标准差 S S S,样本数 n n n;
(3) 样本来自正态或近似正态总体;单样本T检验实例
检验难产儿样本出生体重与一般婴儿出生体重是否相同?已知一般婴儿出生体重 μ 0 = 3.30 k g \mu_0=3.30kg μ0=3.30kg,难产儿样本 n = 35 , X ˉ = 3.42 , S = 0.40 n=35,\bar X=3.42,S=0.40 n=35,Xˉ=3.42,S=0.40①建立假设检验:
H o H_o Ho:难产儿与一般婴儿的体重均数相等, μ = μ 0 \mu = \mu _0 μ=μ0
H 1 H_1 H1:难产儿与一般婴儿的体重均数不相等, μ ≠ μ 0 \mu ≠ \mu _0 μ=μ0②确定显著性水平: α = 0.05 \alpha=0.05 α=0.05
③计算检验统计量: t = X ˉ − μ 0 S / n = 3.42 − 3.30 0.40 / 35 = 1.77 , v = n − 1 = 34 t=\frac{\bar X-\mu_0}{S/\sqrt{n}}=\frac{3.42-3.30}{0.40/\sqrt{35}}=1.77,v=n-1=34 t=S/nXˉ−μ0=0.40/353.42−3.30=1.77,v=n−1=34
④查相应的界表值,确定P值。得 t = 1.77 < 2.032 t=1.77 < 2.032 t=1.77<2.032 故不拒绝原假设,不能认为难产儿平均体重与一般婴儿平均体重不相同
-
配对样本的t检验
配对样本t检验针对配对的两组样本。假设两组样本之间的差值服从正态分布。如果该正态分布的期望为零,则说明这两组样本不存在显著差异。原假设: μ d = 0 \mu_d=0 μd=0配对方式
①自身配对:同一对象接受2种处理,如同一患者接受不同的治疗药物
②异体配对:将条件相近的实验对象配对,并分别给予不同的处理统计量计算:
t = d ˉ S d / n t=\frac{\bar d}{S_d/\sqrt{n}} t=Sd/ndˉ
d ˉ \bar d dˉ:两组样本差值的平均数
S d S_d Sd:两组样本差值的标准差
n n n:配对样本数配对样本T检验实例
某医院用A、B两种血红蛋白法测量16名健康男青年的血红蛋白,问两者有无差别
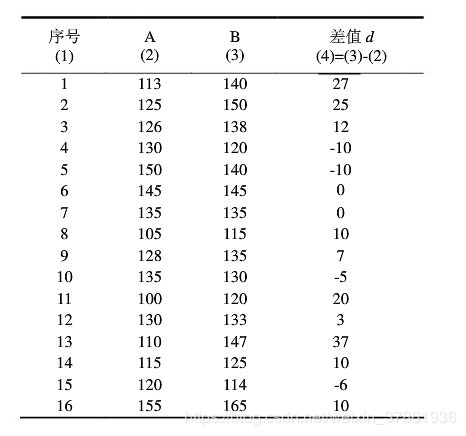
H 0 H_0 H0: μ d = 0 \mu_d=0 μd=0 两种方法测量结果相同
H 0 H_0 H0: μ d ≠ 0 \mu_d≠0 μd=0 两种方法测量结果不相同
显著性水平: α = 0.05 \alpha = 0.05 α=0.05
计算统计量 t = d ˉ S d / n = 8.125 13.735 / 16 = 2.366 t=\frac{\bar d}{S_d/\sqrt{n}}=\frac{8.125}{13.735/\sqrt{16}}=2.366 t=Sd/ndˉ=13.735/168.125=2.366
查相应的界表值,确定P值,拒绝 H 0 H_0 H0,可认为A、B两种测量结果不一致, -
独立样本的t检验
该检验用于检验两组非相关样本均值之间的差异性,从而判断两样本所代表的总体均值是否有差异
统计量计算:
t = X ˉ 1 − X ˉ 2 ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 ( 1 n 1 + 1 n 2 ) t=\frac{\bar X_1-\bar X_2}{\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}} t=n1+n2−2(n1−1)S12+(n2−1)S22(n11+n21)Xˉ1−Xˉ2自由度 v = n 1 + n 2 − 2 v=n_1+n_2-2 v=n1+n2−2
适用条件:
(1)可计算两样本的均值及标准差
(2)样本来自正态或近似正态总体
(3)总体方差齐次 σ 1 2 = σ 2 2 \sigma_1 ^2= \sigma_2^2 σ12=σ22独立样本T检验实例
问独立样本甲和乙均值是否一致?

H 0 H_0 H0: μ 1 = μ 2 \mu_1 = \mu_2 μ1=μ2
H 0 H_0 H0: μ 1 ≠ μ 2 \mu_1 ≠\mu_2 μ1=μ2
显著性水平: α = 0.05 \alpha=0.05 α=0.05
计算统计量 t = X ˉ 1 − X ˉ 2 ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 ( 1 n 1 + 1 n 2 ) = − 3.785 t=\frac{\bar X_1-\bar X_2}{\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}}=-3.785 t=n1+n2−2(n1−1)S12+(n2−1)S22(n11+n21)Xˉ1−Xˉ2=−3.785
v = 10 + 10 − 2 = 18 v=10+10-2=18 v=10+10−2=18
查表得拒绝原假设,可以认为 μ 1 ≠ μ 2 \mu_1 ≠\mu_2 μ1=μ2
5、F检验
F检验也称为方差齐次性检验
方差为样本标准差的平方,即: S 2 = ∑ i n ( x i − x ˉ ) 2 / ( n − 1 ) S^2=∑_i^n(x_i-\bar x)^2/(n-1) S2=∑in(xi−xˉ)2/(n−1)
两组数据就能得到两个 S 2 S^2 S2值
F = S 1 2 / S 2 2 F=S_1^2/S_2^2 F=S12/S22
然后计算的F值与查表得到的F表值比较,如果
F < F表 表明两组数据没有显著差异;
F ≥ F表 表明两组数据存在显著差异。
