David Silver 强化学习Lecture4：Model-Free Prediction

    David Silver强化学习系列博客的内容整理自David Silver 强化学习的PPT和知乎叶强强化学习专栏。

1 Introduction

    前三节笔记中，通过动态规划能够解决环境已知的MDP问题，也就是已知 <S,A,P,R,γ> < S , A , P , R , γ > ，已知environment即已知转移矩阵 P P 与reward函数 R R 。但是很多问题中environment是未知的，不清楚做出了某个action之后会变到哪一个state，也不知道这个action好还是不好，在这种情况下需要解决的prediction和control问题就是Model-free prediction和Model-free control。显然这种新的问题只能从与environment的交互得到的experience中获取信息。
    这一章节笔记要解决的问题是Model-free prediction，即未知environment的Policy evaluation，在给定的policy下，求解每个state的value function是多少。

2 Monte-Carlo Learning

2.1 Monte-Carlo Reinforcement Learning

    蒙特卡罗强化学习 (Monte-Carlo reinforcement learning, MC 学习)： 指在不清楚 MDP 状态转移概率和即时奖励的情况下，直接从经历完整的状态序列 (episode) 来估计状态的真实价值，通常情况下某状态的价值等于在多个episode中以该状态算得到的所有收获的平均。
    完整的状态序列 (complete episode)：指从某一个状态开始，agent与环境交互直到终止状态，环境给出终止状态的奖励为止。完整的状态序列不要求起始状态一定是某一个特定的状态，但是要求个体最终进入环境认可的某一个终止状态。
    比如，现评估某状态 s s 的价值函数。我们采样了两个episode，从一个episode里面得到的回报是5，然后下一个episode里面的得到的回报是7，我们可以从起始状态来评估此状态的价值函数=（5+7）/2=6。
    注：收获不是针对Episode的，它存在于Episode内，针对于Episode中某一个状态。从这个状态开始经历完Episode时得到的有衰减的即时奖励的总和。从一个Episode中，我们可以得到该Episode内所有状态的收获。当一个状态在Episode内出现多次，该状态的收获有不同的计算方法，下文会讲到。
    蒙特卡罗强化学习有如下特点：不依赖状态转移概率，直接从经历过的完整的状态序列中学习，使用的思想就是用平均收获值代替状态价值。理论上完整的状态序列越多，结果越准确。

2.2 Monte-Carlo Policy Evaluation

    我们可以使用蒙特卡罗强化学习来评估一个给定的策略。基于特定策略 π π 的一个 Episode信息可以表示为如下的一个序列： S1,A1,R2,S2,A2,...,St,At,Rt+1,...,Sk∼π S 1 , A 1 , R 2 , S 2 , A 2 , . . . , S t , A t , R t + 1 , . . . , S k ∼ π
    其中， Rt+1 R t + 1 表示agent在状态 St S t 执行一个行为 At A t 后，离开该状态获得的即时奖励。很多时候，即时奖励只出现在Episode结束状态时，但不能否认在中间状态也可能有即时奖励。
     t t 时刻状态 St S t 的收获可以表述为： Gt=Rt+1+γRt+2+...+γT−1RT G t = R t + 1 + γ R t + 2 + . . . + γ T − 1 R T
    其中， T T 为终止时刻。该策略下某一状态 s s 的价值： vπ(s)=Eπ[Gt|St=s]≈∑i=tNGiN v π ( s ) = E π [ G t | S t = s ] ≈ ∑ i = t N G i N
    在Monte-Carlo policy evaluation中，价值函数的取值从期望简化成了均值。当 N N 逼近 ∞ ∞ 时，我们可以得到确切的函数期望值。

2.3 First-Visit Monte-Carlo Policy Evaluation

    不难发现，在蒙特卡罗算法评估策略时要针对多个包含同一状态的完整状态序列求收获继而再取收获的平均值。如果一个完整的状态序列中某一需要计算的状态出现在序列的多个位置，也就是说个体在与环境交互的过程中从某状态出发后又一次或多次返回到该状态。在这种情况下，根据收获的定义，在一个状态序列下，不同时刻的同一状态其计算得到的收获值是不一样的。我们有两种方法可以选择，一是仅把状态序列中第一次出现该状态时的收获值纳入到收获平均值的计算中；另一种是针对一个状态序列中每次出现的该状态，都计算对应的收获值并纳入到收获平均值的计算中。两种方法对应的蒙特卡罗评估分别称为：首次访问 (frst visit) 和每次访问 (every visit) 蒙特卡罗评估。
    首次访问蒙特卡罗评估： 给定一个策略，使用一系列完整Episode评估某一个状态s时，对于每一个Episode，仅当该状态第一次出现时列入计算。
    假设有 n n 个episode，评估状态 s s 。对于第一个episode，查找该episode中 s s 第一次出现的位置，如果该episode中存在状态 s s ，则计数器 N(s) N ( s ) 加1，并计算此时该状态的收获值 Gt G t 。对于第二个episode，也是如此…统计完 n n 个episode后，计算平均值。

2.4 Every-Visit Monte-Carlo Policy Evaluation

    每次访问 (every visit) 蒙特卡罗评估：在给定一个策略，使用一系列完整Episode评估某一个状态 s s 时，对于每一个Episode，计算 s s 的每一次出现的平均值。

    
    在本算法中，不论是首次访问还是每次访问，都需要记录两个值：
    状态s被访问到的次数N(s)，每次访问时return之和S(s)；遍历完所有的episode之后，得到状态s的价值函数V(s)。
    其中，首次访问是在一个episode中只记录第一次访问到的s；每次访问是在一个episode中每次访问到s都记录下来。

2.5 Incremental Mean

    在使用蒙特卡洛方法求解平均收获时，需要计算平均值。通常计算平均值要预先存储所有的数据，最后使用总和除以此次数。这里介绍了一种更简单实用的方法，使得在计算平均收获时不需要存储所有既往收获，而是每得到一次收获，就计算其平均收获。

    累进更新平均值利用前一次的平均值和当前数据以及数据总个数来计算新的平均值。把这个方法应用于蒙特卡洛策略评估，就得到下面的蒙特卡洛累进更新。

3 Temporal-Difference Learning

    和蒙特卡洛学习一样，它也从Episode学习，不需要了解模型本身；但是它可以学习不完整的Episode，通过合理的引导（bootstrapping），先估计某状态在该状态序列完整后可能得到的收获，并在此基础上利用前文所述的累进更新平均值的方法得到该状态的价值，再通过不断的采样来持续更新这个价值。
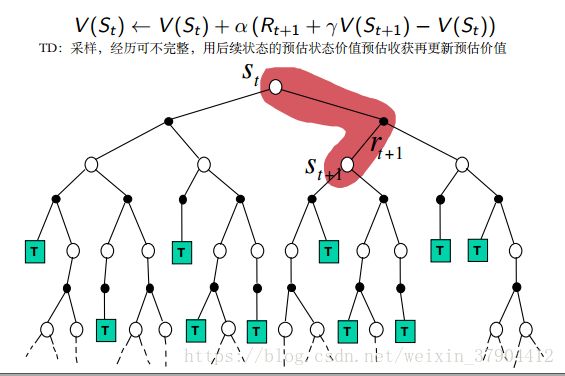
    具体地说，在 TD 学习中，算法在估计某一个状态的收获时，用的是离开该状态的即时奖励 Rt+1 R t + 1 与下一时刻状态 St+1 S t + 1 的预估状态价值乘以衰减系数 γ γ 组成：
v(St)←v(St)+α(Rt+1+γv(St+1)−V(St)) v ( S t ) ← v ( S t ) + α ( R t + 1 + γ v ( S t + 1 ) − V ( S t ) )
    其中， Rt+1+γv(St+1) R t + 1 + γ v ( S t + 1 ) 称为TD目标值， Rt+1+γv(St+1)−V(St) R t + 1 + γ v ( S t + 1 ) − V ( S t ) 称为TD误差。
    引导 (bootstrapping)：指的是用 TD 目标值代替收获 Gt 的过程。

3.1 MC and TD

    MC和TD学习使用的都是通过个体与环境实际交互生成的一系列状态序列来更新状态的价值。这在解决大规模问题或者不清楚环境动力学特征的问题时十分有效。不过MC学习和TD学习两者也是有着很明显的差别的。
    下面通过一个例子来详细阐述这两种学习方法各自的特点。

    想象一下作为个体的你如何预测下班后开车回家这个行程所花费的时间。在回家的路上你会依次经过一段高速公路、普通公路、和你家附近街区三段路程。由于你经常开车上下班，在下班的路上多次碰到过各种情形，比如取车的时候发现下雨，高速路况的好坏、普通公路是否堵车等等。在每一种状态下时，你对还需要多久才能到家都有一个经验性的估计。表 1 的“既往经验预计（仍需耗时）”列给出了这个经验估计，这个经验估计基本反映了各个状态对应的价值，通常你对下班回家总耗时的预估是 30 分钟。
    假设你现在又下班准备回家了，当花费了 5 分钟从办公室到车旁时，发现下雨了。此时根据既往经验，估计还需要 35 分钟才能到家，因此整个行程将耗费 40 分钟。随后你进入了高速公路，高速公路路况非常好，你一共仅用了 20 分钟就离开了高速公路，通常根据经验你只再需要 15 分钟就能到家，加上已经过去的 20 分钟，你将这次返家预计总耗时修正为 35 分钟，比先前的估计少了 5 分钟。但是当你进入普通公路时，发现交通流量较大，你不得不跟在一辆卡车后面龟速行驶，这个时候距离出发已经过去 30 分钟了，根据以往你路径此段的经验，你还需要10 分钟才能到家，那么现在你对于回家总耗时的预估又回到了 40 分钟。最后你在出发 40 分钟后到达了家附近的街区，根据经验，还需要 3 分钟就能到家，此后没有再出现新的情况，最终你在 43 分钟的时候到达家中。经历过这一次的下班回家，你对于处在途中各种状态下返家的还需耗时（对应于各状态的价值）有了新的估计，但分别使用 MC 算法和 TD 算法得到的对于各状态返家还需耗时的更新结果和更新时机都是不一样的。
    如果使用 MC 算法，在整个驾车返家的过程中，你对于所处的每一个状态，例如“取车时下雨”，“离开高速公路”，“被迫跟在卡车后”、“进入街区”等时，都不会立即更新这些状态对应的返家还需耗时的估计，这些状态的返家仍需耗时仍然分别是先前的 35 分钟、 15 分钟、 10 分钟和 3 分钟。但是当你到家发现整个行程耗时 43 分钟后，通过用实际总耗时减去到达某状态的已耗时，你发现在本次返家过程中在实际到达上述各状态时，仍需时间则分别变成了： 38 分钟（43-5）、23 分钟（43-20）、 13 分钟（43-30）和 3 分钟（43-40）。如果选择修正系数为 1，那么这些新的耗时将成为今后你在各状态时的预估返家仍需耗时，相应的整个行程的预估耗时被更新为 43 分钟。
    如果使用 TD 算法，则又是另外一回事，当取车发现下雨时，同样根据经验你会认为还需要35 分钟才能返家，此时，你将立刻更新对于返家总耗时的估计，为仍需的 35 分钟加上你离开办公室到取车现场花费的 5 分钟，即 40 分钟。同样道理，当驶离高速公路，根据经验，你对到家还需时间的预计为 15 分钟，但由于之前你在高速上较为顺利，节省了不少时间，在第 20 分钟时已经驶离高速，实际从取车到驶离高速只花费了 15 分钟，则此时你又立刻更新了从取车时下雨到到家所需的时间为 30 分钟，而整个回家所需时间更新为 35 分钟。当你在驶离高速在普通公路上又行驶了 10 分钟被堵，你预计还需 10 分钟才能返家时，你对于刚才驶离高速公路返家还需耗时又做了更新，将不再是根据既往经验预估的 15 分钟，而是现在的 20 分钟，加上从出发到驶离高速已花费的 20 分钟，整个行程耗时预估因此被更新为 40 分钟。直到你花费了 40 分钟只到达家附近的街区还预计有 3 分钟才能到家时，你更新了在普通公路上对于返家还需耗时的预计为 13 分钟。最终你按预计 3 分钟后进入家门，不再更新剩下的仍需耗时。

3.2 Advantages and Disadvantages of MC vs. TD

    通过比较可以看出， MC 算法只在整个行程结束后才更新各个状态的仍需耗时，而 TD 算法则每经过一个状态就会根据在这个状态与前一个状态间实际所花时间来更新前一个状态的仍需耗时。
    TD 学习能比 MC 学习更快速灵活的更新状态的价值估计，这在某些情况下有着非常重要的实际意义。回到驾车返家这个例子中来，我们给驾车返家制定一个新的目标，不再以耗时多少来评估状态价值，而是要求安全平稳的返回家中。假如有一次你在驾车回家的路上突然碰到险情：对面开过来一辆车感觉要和你迎面相撞，严重的话甚至会威胁生命，不过由于最后双方驾驶员都采取了紧急措施没有让险情实际发生，最后平安到家。如果是使用蒙特卡罗学习，路上发生的这一险情可能引发的极大负值奖励将不会被考虑，你不会更新在碰到此类险情时的状态的价值；但是在 TD 学习时，碰到这样的险情过后，你会立即大幅调低这个状态的价值，并在今后再次碰到类似情况时采取其它行为，例如降低速度等来让自身处在一个价值较高的状态中，尽可能避免发生意外事件的发生。

    通过驾车返家这个例子，我们应该能够认识到： TD 学习在知道结果之前就可以学习，也可以在没有结果时学习，还可以在持续进行的环境中学习，而 MC 学习则要等到最后结果才能学习。 TD 学习在更新状态价值时使用的是 TD 目标值，即基于即时奖励和下一状态的预估价值来替代当前状态在状态序列结束时可能得到的收获，它是当前状态价值的有偏估计，而 MC 学习则使用实际的收获来更新状态价值，是某一策略下状态价值的无偏估计。 TD 学习存在偏差 (bias)的原因是在于其更新价值时使用的也是后续状态预估的价值，如果能使用后续状态基于某策略的真实 TD 目标值 (true TD target) 来更新当前状态价值的话，那么此时的 TD 学习得到的价值也是实际价值的无偏估计。虽然绝大多数情况下 TD 学习得到的价值是有偏估计的，但是其方差 (Variance) 却较 MC 学习得到的方差要低，且对初始值敏感，通常比 MC 学习更加高效，这也主要得益于 TD 学习价值更新灵活，对初始状态价值的依赖较大。
    继续通过一个示例来剖析 TD 学习和 MC 学习的特点。
    假设在一个强化学习问题中有 A 和 B 两个状态，模型未知，不涉及策略和行为，只涉及状态转换和即时奖励，衰减系数为 1。现有如下表所示 8 个完整状态序列的经历，其中除了第 1 个状态序列发生了状态转移外，其余 7 个完整的状态序列均只有一个状态构成。现要求根据现有信息计算状态 A、 B 的价值分别是多少？

    我们考虑分别使用 MC 算法和 TD 算法来计算状态 A、 B 的价值。
    首先考虑 MC 算法，在8 个完整的状态序列中，只有第一个序列中包含状态 A，因此 A 价值仅能通过第一个序列来计算，也就等同于计算该序列中状态 A 的收获：
V(A)=G(A)=RA+γRB=0 V ( A ) = G ( A ) = R A + γ R B = 0
    状态 B 的价值，则需要通过状态 B 在 8 个序列中的收获值来平均。因为状态B没有后续可转移的状态，即 R(B′)=0，V(B′)=0 R ( B ′ ) = 0 ， V ( B ′ ) = 0 ，因此其结果是 6/8。
V(B)=18∑i=18Gi(B)=18∑i=18(RB+γR(B′)=18(0+1∗6+0)=68 V ( B ) = 1 8 ∑ i = 1 8 G i ( B ) = 1 8 ∑ i = 1 8 ( R B + γ R ( B ′ ) = 1 8 ( 0 + 1 ∗ 6 + 0 ) = 6 8
    因此在使用 MC 算法时，状态 A、 B 的价值分别为 6/8 和 0
    再来考虑应用 TD 算法。TD算法试图利用现有的Episode经验构建一个MDP（如下图），由于存在一个Episode使得状态A有后继状态B，因此状态A的价值是通过状态B的价值来计算的，同时经验表明A到B的转移概率是100%，且A状态的即时奖励是0，并且没有衰减，因此A的状态价值等于B的状态价值。

    计算过程如下，可以看成一个MDP，求状态价值函数。
V(A)=π(a|A)[RaA+γPaABV(B)]=1∗[0+1∗1∗V(B)]=V(B) V ( A ) = π ( a | A ) [ R A a + γ P A B a V ( B ) ] = 1 ∗ [ 0 + 1 ∗ 1 ∗ V ( B ) ] = V ( B )
V(B)=π(b1|B)[Rb1B+γPb1BB′V(B′)]+π(b2|B)[Rb2B+γPb2BB′V(B′)]=0.75∗[1+1∗1∗0]+0.25∗[0+1∗1∗0]=0.75 V ( B ) = π ( b 1 | B ) [ R B b 1 + γ P B B ′ b 1 V ( B ′ ) ] + π ( b 2 | B ) [ R B b 2 + γ P B B ′ b 2 V ( B ′ ) ] = 0.75 ∗ [ 1 + 1 ∗ 1 ∗ 0 ] + 0.25 ∗ [ 0 + 1 ∗ 1 ∗ 0 ] = 0.75
    因此在使用 TD 算法时，状态 A、 B 的价值均为 6/8。

3.3 Certainty Equivalence

MC算法

    MC算法试图收敛至一个能够最小化状态价值与实际收获的均方差的解决方案，这一均方差用公式表示为： ∑k=1K∑t=1Tk(Gkt−V(Skt))2 ∑ k = 1 K ∑ t = 1 T k ( G t k − V ( S t k ) ) 2
    其中， k k 表示的是Episode序号， K K 为总的Episode数量， t t 为一个Episode内状态序号（第1,2,3…个状态等）， Tk T k 表示的是第 k k 个Episode总的状态数， Gkt G t k 表示第 k k 个Episode里 t t 时刻状态 St S t 获得的最终收获， V(Skt) V ( S t k ) 表示的是第 k k 个Episode里算法估计的 t t 时刻状态 St S t 的价值。

TD算法

    TD算法则收敛至一个根据已有经验构建的最大可能的马尔科夫模型的状态价值，也就是说TD算法将首先根据已有经验估计状态间的转移概率：

    同时估计某一个状态的即时奖励：

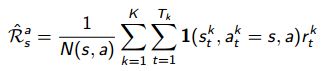
    最后计算该MDP的状态函数。

3.4 Unified View

    通过上面的示例，我们能体会到 TD 算法与 MC 算法之间的另一个差别： TD 算法使用了MDP 问题的马尔科夫属性，在具有马尔科夫性的环境下更有效；但是 MC 算法并不利用马尔科夫属性，适用范围不限于具有马尔科夫性的环境。
    现在为止所阐述的蒙特卡罗 (MC) 学习算法、时序差分 (TD) 学习算法和上一篇讲述的动态规划(DP) 算法都可以用来计算状态价值。他们它们的特点也是十分鲜明的，MC和TD是两种在不依赖模型的情况下的常用方法，这其中又以 MC 学习需要完整的状态序列来更新状态价值， TD 学习则不需要完整的状态序列； DP 算法则是基于模型的计算状态价值的方法，它通过计算一个状态 S 所有可能的转移状态 S’ 及其转移概率以及对应的即时奖励来计算这个状态 S 的价值。
    在是否使用引导数据上， MC 学习并不使用引导数据，它使用实际产生的奖励值来计算状态价值； TD 和 DP 则都是用后续状态的预估价值作为引导数据来计算当前状态的价值。
    在是否采样的问题上， MC 和 TD 不依赖模型，使用的都是个体与环境实际交互产生的采样状态序列来计算状态价值的，而 DP 则依赖状态转移概率矩阵和奖励函数，全宽度计算状态价值，没有采样之说。
    下图，非常直观的体现了三种算法的区别。

MC算法

TD算法

DP算法

    综合上述三种学习方法的特点，可以小结如下：当使用单个采样，同时不经历完整的状态序列更新价值的算法是 TD 学习；当使用单个采样，但依赖完整状态序列的算法是 MC 学习；当考虑全宽度采样，但对每一个采样经历只考虑后续一个状态时的算法是 DP 学习；如果既考虑所有状态转移的可能性，同时又依赖完整状态序列的，那么这种算法是穷举 (exhausive search) 法。需要说明的是： DP 利用的是整个 MDP 问题的模型，也就是状态转移概率，虽然它并不实际利用采样经历，但它利用了整个模型的规律，因此也被认为是全宽度 (full width) 采样的。

4 TD(λ)

4.1 n-Step Prediction

    先前所介绍的 TD 算法实际上都是 TD(0) 算法，括号内的数字 0 表示的是在当前状态下往前多看 1 步，要是往前多看 2 步更新状态价值会怎样？这就引入了 n-步预测的概念。

    n-步预测指从状态序列的当前状态 ( St S t ) 开始往序列终止状态方向观察至状态 St+n−1 S t + n − 1 ，使用这 n n 个状态产生的即时奖励 (Rt+1,Rt+2,...,Rt+n) ( R t + 1 , R t + 2 , . . . , R t + n ) 以及状态 St+n S t + n 的预估价值来计算当前状态 St S t 的价值。

4.2 n-Step Return

    TD 是 TD(0) 的简写，是基于1-步预测的。根据 n-步预测的定义，可以推出当 n=1,2 和 ∞ ∞ 时对应的预测值如下表所示。从该表可以看出， MC 学习是基于 ∞ ∞ -步预测的。

    定义 n-步收获为： G(n)t=Rt+1+γRt+2+...+γn−1Rt+n+γnV(St+n) G t ( n ) = R t + 1 + γ R t + 2 + . . . + γ n − 1 R t + n + γ n V ( S t + n )
    由此可以得到 n-步 TD 学习对应的状态价值函数的更新公式为：
V(St)←V(St)+α(G(n)t−V(St)) V ( S t ) ← V ( S t ) + α ( G t ( n ) − V ( S t ) )

4.3 Forward View of TD(λ)

    当 n=1 n = 1 时等同于 TD(0) 学习， n 取无穷大时等同于 MC 学习。由于 TD 学习和 MC 学习又各有优劣，那么会不会存在一个 n n 值使得预测能够充分利用两种学习的优点或者得到一个更好的预测效果呢？研究认为不同的问题其对应的比较高效的步数不是一成不变的。选择多少步数作为一个较优的计算参数是需要尝试的超参数调优问题。
    为了能在不增加计算复杂度的情况下综合考虑所有步数的预测，我们引入了一个新的参数 λ λ 。并定义 λ λ 收获。

λ λ 收获

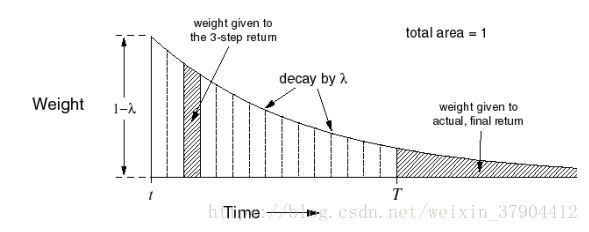
     λ λ 收获 Gλt G t λ 综合考虑了从 1 1 到 ∞ ∞ 的所有步收获的和，它给其中的任意一个 n− n − 步收获施加一定的权重 (1−λ)λn−1 ( 1 − λ ) λ n − 1 。通过这样的权重设计，得到如下的公式：
Gλt=(1−λ)∑n=1∞λn−1G(n)t G t λ = ( 1 − λ ) ∑ n = 1 ∞ λ n − 1 G t ( n )
    对应的 λ λ 预测写成TD(λ)： V(St)←V(St)+α(G(λ)t−V(St)) V ( S t ) ← V ( S t ) + α ( G t ( λ ) − V ( S t ) )
    下图是各步收获的权重分配图，图中最后一列 λ λ 的指数是 T−t−1 T − t − 1 。 T T 为终止状态的时刻步数， t t 为当前状态的时刻步数，所有的权重加起来为 1 1 。

    下图显示了 TD(λ) 中对于 n-收获的权重分配，左侧阴影部分是 3-步收获的权重值，随着n的增大，其 n-收获的权重呈几何级数的衰减。当在 T T 时刻到达终止状态时，未分配的权重 (右侧阴影部分) 全部给予终止状态的实际收获值。如此设计可以使一个完整的状态序列中所有的 n-步收获的权重加起来为 1，离当前状态越远的收获其权重越小。

    前向认识 TD(λ)
    TD(λ) 的设计使得在状态序列中，一个状态的价值 V(St) V ( S t ) 由 G(λ)t G t ( λ ) 得到，而后者又间接由所有后续状态价值计算得到，因此可以认为更新一个状态的价值需要知道所有后续状态的价值。也就是说，必须要经历完整的状态序列获得包括终止状态的每一个状态的即时奖励才能更新当前状态的价值。这和 MC 算法的要求一样，因此 TD(λ) 算法有着和 MC 方法一样的劣势。 λ λ 取值区间为 [0,1]，当 λ=1 λ = 1 时对应的就是 MC 算法。这个实际计算带来了不便。

4.4 Backward View TD(λ)

    反向认识 TD(λ) 为 TD(λ) 算法进行在线实时单步更新学习提供了理论依据。为了解释这一点，需要先引入“效用迹”这个概念。我们通过一个之前的一个例子来解释这个问题。老鼠在依次连续接受了 3 次响铃和 1 次亮灯信号后遭到了电击，那么在分析遭电击的原因时，到底是响铃的因素较重要还是亮灯的因素更重要呢？

    如果把老鼠遭到电击的原因认为是之前接受了较多次数的响铃，则称这种归因为频率启发式(原因归因于出现频率最高的状态)；而把电击归因于最近少数几次状态的影响，则称为就近启发式(将原因归因于较近的几次状态)。
    如果给每一个状态引入一个数值： 效用 (eligibility, E) 来表示该状态对后续状态的影响，就可以同时利用到上述两个启发。而所有状态的效用值总称为效用迹 (eligibility traces,ES)。
    定义：
     E0(s)=0 E 0 ( s ) = 0
     Et(s)=γλEt−1(s)+1(St=s) E t ( s ) = γ λ E t − 1 ( s ) + 1 ( S t = s )
    其中 1(St=s) 1 ( S t = s ) 是一个条件判断表达式，表示当 St=s S t = s 时取值为 1，其余条件下取值为 0。
    下图给出了效用E对于时间t的一个可能的曲线：

    该图横坐标是时间，横坐标下有竖线的位置代表当前时刻的状态为 s，纵坐标是效用的值E。可以看出当某一状态连续出现， E 值会在一定衰减的基础上有一个单位数值的提高，此时认为该状态将对后续状态的影响较大，如果该状态很长时间没有经历，那么该状态的的 E 值将逐渐趋于 0，表明该状态对于较远的后续状态价值的影响越来越少。
    需要指出的是，针对每一个状态存在一个 E 值，且 E 值并不需要等到状态序列到达终止状态才能计算出来，它是根据已经经过的状态序列来计算得到，并且在每一个时刻都对每一个状态进行一次更新。 E 值存在饱和现象，有一个瞬时最高上限： Emax=11−γλ E m a x = 1 1 − γ λ
    E 值是一个非常符合神经科学相关理论的、非常精巧的设计。可以把它看成是神经元的一个参数，它反映了神经元对某一刺激的敏感性和适应性。神经元在接受刺激时会有反馈，在持续刺激时反馈一般也比较强，当间歇一段时间不刺激时，神经元又逐渐趋于静息状态；同时不论如何增加刺激的频率，神经元有一个最大饱和反馈。
    如果我们在更新状态价值时把该状态的效用同时考虑进来，那么价值更新可以表示为：

    当 λ=0 λ = 0 时， St=s S t = s 一直成立，此时价值更新等同于 TD(0) 算法：
V(St)←V(St)+αδt V ( S t ) ← V ( S t ) + α δ t
    当 λ=1 λ = 1 时，在每完成一个状态序列后更新状态价值时，其完全等同于 MC 学习；但在引入了效用迹后，可以每经历一个状态就更新状态的价值，这种实时更新的方法并不完全等同于MC。
    当 λ∈(0,1) λ ∈ ( 0 , 1 ) 时，在每完成一个状态序列后更新价值时，基于前向认识的 TD(λ) 与基于反向认识的 TD(λ) 完全等效；不过在进行在线实时学习时，两者存在一些差别。