遗传算法求解函数优化问题-基本遗传算法SGA
博客内图片文字来源于书本《遗传算法及其应用》
1.算法介绍
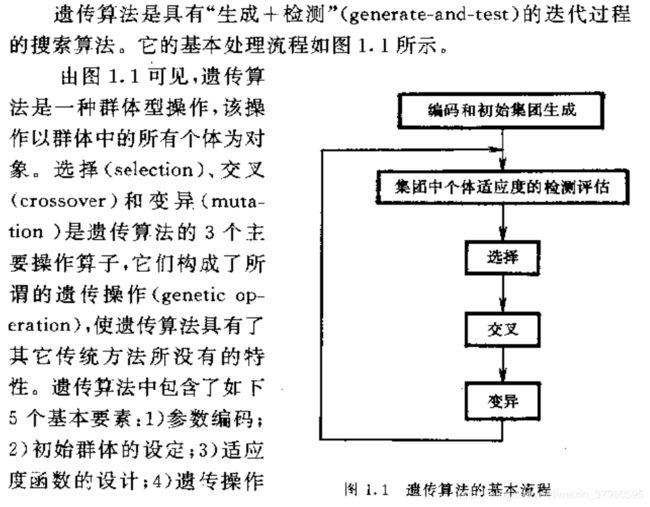





《遗传算法及其应用》是在阅读GA过程中较好的一本算法基础方法介绍的书,想要从零开始详细的进行学习的同学们,这是很好的参考工具。
关于遗传算法,《遗传算法及其应用》一书给出了最为详尽的描述,书中也针对不同问题给出了基础的方法,例如组合优化问题中的函数优化、背包问题、货郎担问题和图论等等。
2.实例介绍
在上述内容的基础上,使用C++对函数优化问题进行求解,便于了解GA算法。这里使用的函数优化问题是无约束问题。
函数案例为:
min Z
Z=(1.5-x_1+x_1*x_2)^2+(2.25-x_1+x_1*(x_2)^2)^2+(2.625-x_1+x_1*(x_2)^3)^2
x->[-4.5,4.5]
最优解:Z(3,0.5)=0
2.1 编码
在示例函数当中,变量x_1和x_2均属于区间[-4.5,4.5]。使用二进制无符号整数进行编码,将变量约束空间映射到遗传空间。
为了更详细的表示遗传空间,以下使用8位二进制对变量进行编码,则编码空间整体位16位,其中前8位表示x_1的编码,其余表示x_2。
当然,这里使用5位编码也是可以的,只要能够包含约束区域即可。
2.2 解码
在2.1当中对变量进行了编码,这种编码从0000 0000开始,到1111 1111结束。
一般情况下0000 0000表示数值0,0000 00001表示数值1,以此类推。显然,无法将编码与约束进行一一对应。那么约束空间的负数和小数空间该如何进行表示呢?
假设约束空间的上限为b,下限为a,编码长度l,二进制编码转化为十进制值为x_t,实际值为x,则有:
x=a+(x_t *(b-a))/(2^l -1)
使用该方法对编码进行解码。解码方法如下:
void Decode(int X[person_number][node],int pers) {
int X_temp = 0;
for (int i = 0; i < 8; i++) {
X_temp += X[pers][i] * pow(2, 8 - 1 - i);
}
x_code[pers][0] = XMIN + XMIN + (X_temp*(XMAX - XMIN)) / (pow(2, 8) - 1);
X_temp = 0;
for (int i = 8; i < 16; i++) {
X_temp += X[pers][i] * pow(2, 16 - 1 - i);
}
x_code[pers][1] = XMIN + (X_temp*(XMAX - XMIN)) / (pow(2, 8) - 1);
}
为什么编码后,还需要进行解码呢?原因是将二进制码串转化为约束空间内的十进制值,便于适应度函数进行计算。
2.3 产生初始群体
对于初始群体,只需要使用rand()函数生成对应的0或1即可。
初始群体为:
void initial() {
srand((unsigned int)time(NULL));
for (int i = 0; i < person_number;i++) {
for (int j = 0; j < node;j++) {
X_code[i][j] = (rand() % (1 + 1));
}
}
}
2.4 轮盘赌选择
假设群体的适应性由一个转轮代表。
每一个染色体指定转轮中一个区域。区域的大小与该染色体的适应性分数成正比,适应性分数越高,它在转轮中对应的区域面积也越大。
为了选取一个染色体,要做的就是旋转这个轮子,当转轮停止时,指针停止在哪一区域上,就选中与它对应的那个染色体。
在这里,假设个体适应值为f_i;则个体的选择概率是f_i/sum(f_i),概率越大,被选择的可能就越大,然后计算累积概率。
工作时,使用rand()函数生成0-1之间的小数,查看小数落在哪一累积概率区间,则选择该个体。
具体工作过程如下:
void Roulette() {
double fit_sum = 0;//适应值之和
for (int i = 0; i < person_number; i++) {
fit_temp[i] = Fitness(x_code, i);
fit_sum += fit_temp[i];
}
//注意:目标函数是取最小值,那么适应值越小,选择的概率越高
double fit_temp1[person_number];
double fit_sum1 = 0;//修改适应值之和
for (int i = 0; i < person_number; i++) {
fit_temp1[i]=fit_sum - fit_temp[i];//调整适应值为(和-适应值)
fit_sum1 += fit_temp1[i];
}
/*cout << "适应值:" << endl;
for (int i = 0; i < person_number; i++) {
cout<< fit_temp[i]<<" ";
}
cout << endl << "适应值和:" << fit_sum1 << endl;*/
for (int i = 0; i < person_number; i++) {
pro_select[i] = (int((fit_temp1[i] / fit_sum1)*1000000))/1000000.0;
}
pro_cumul[0] = pro_select[0];
for (int i = 1; i < person_number; i++) {
pro_cumul[i] = pro_cumul[i-1]+pro_select[i];
}
pro_cumul[person_number-1] = 1.0;
}
2.5 选择
选择操作的本质为优胜略汰,选择原则是轮盘赌方法,选择的目的是将个体两两配对,放入交配池中,等待交配生成子代。
选择操作为:
void Selection() {
Roulette();//确定选择概率
for (int i = 0; i < person_number;i++) {
for (int j = 0; j < dimension;j++) {
per_cross[i][j] = -1;//初始化配对数组->满足交叉和变异的个体
}
}
//除了复制个体以外,两两配对:产生随机数->确定标号
//两两配对
srand((unsigned int)time(NULL));
for (int i = 0; i < person_number/2;i++) {
for (int j = 0; j < 2;j++) {
double temp = (rand() % (10000 + 1)) / 10000.0;
//查询下标
if (temp <= pro_cumul[0]) {
per_cross[i][j] = 0;
}
else {
for (int k = 0; k < person_number - 1; k++) {
if (temp > pro_cumul[k]) {
if (temp <= pro_cumul[k + 1]) {
per_cross[i][j] = k + 1;
break;
}
}
}
}
}
}
/*cout << "交配池:" << endl;
for (int i = 0; i < person_number / 2; i++) {
for (int j = 0; j < 2; j++) {
cout << per_cross[i][j] << " ";
}
cout << endl;
}
cout << endl;*/
}
2.6 复制
复制的目的是保留最佳个体基因,将其保留到子代,有利于减少迭代次数。
复制操作为:
void Copy(double fit_temp[person_number]) {
//确定复制个体
double fit_temp1[person_number];//临时适应值数组
for (int i = 0; i < person_number; i++) {
fit_temp1[i] = fit_temp[i];
}
//适应值排序->由小到大
int fit_index[person_number];//适应值编号
for (int i = 0; i < person_number; i++) {
fit_index[i] = i;
}
for (int i = 1; i < person_number; i++) {
for (int j = 0; j < person_number - i; j++) {
if (fit_temp1[j + 1] < fit_temp1[j]) {
double temp1 = fit_temp1[j];
int temp2 = fit_index[j];
fit_temp1[j] = fit_temp1[j + 1];
fit_index[j] = fit_index[j + 1];
fit_temp1[j + 1] = temp1;
fit_index[j + 1] = temp2;
}
}
}
//确定复制个体->与目标函数有关,这里复制最小的个体
per_copy[0] = fit_index[0];
fitness_temp = fit_temp1[0];
//cout << endl << "适应值:"<< fit_temp1[0]<<" "<<"最佳个体基因:" << per_copy[0] << endl;
}
2.7 交叉
交叉是GA算法的重要操作。
在这里,使用二点交叉方法。二点交叉为:

若交配个体中含有最佳个体,则最佳个体直接复制到子代;交配对象的子代由最佳个体的交换部分加上自身未交换部分。
交叉操作为:
void Cross() {//二点交叉方法
//若复制个体与其他进行交叉,则复制为下一代,同时交叉一次(两种交叉结果中保留复制个体为主的子代)
//复制-》确定交叉点-》交叉
Copy(fit_temp);//确定复制个体
int X_code_tem[person_number][node];//临时二进制编码值
for (int i = 0; i < person_number;i++) {
for (int j = 0; j < node;j++) {
X_code_tem[i][j] = X_code[i][j];
}
}
srand((unsigned int)time(NULL));
int count = 0;//计数
for (int i = 0; i < person_number / 2;i++) {
double r1 = (rand() % (100 + 1)) / 100.0;
//cout <
int temp[node];//中转
for (int j = 0; j < node; j++) {
temp[j] = 0;
}
int X_code_tem1[2][node];
for (int m = 0; m < 2; m++) {
for (int n = 0; n < node; n++) {
X_code_tem1[m][n] = 0;
}
}
//cout << endl << "配对基因:"<
if (r1 < pc) {//可以进行交叉
//确定交叉点
int cross_section[2];//存放交叉点->小号在前
cross_section[0] = rand() % (15 + 1);
cross_section[1] = rand() % (15 + 1);
if ((cross_section[0] == cross_section[1]) && (cross_section[0] == 0))
cross_section[1] += 1;
if ((cross_section[0] == cross_section[1]) && (cross_section[0] == 15))
cross_section[1] -= 1;
if (cross_section[0] > cross_section[1]) {
swap(cross_section[0], cross_section[1]);
}
//cout << endl << "交叉点:" << cross_section[0]<<" "<< cross_section[1] << endl;
//有最佳基因
if ((per_cross[i][0]==per_copy[0])&&(per_cross[i][1]!=per_copy[0])) {//有其中一个
for (int j = 0; j < node; j++) {
X_code_tem1[0][j] = X_code_tem[per_cross[i][0]][j];
X_code_tem1[1][j] = X_code_tem[per_cross[i][1]][j];
}
/*cout << endl;
for (int k = 0; k < 2; k++) {
for (int j = 0; j < node; j++) {
cout << X_code_tem1[k][j] << " ";
}
cout << endl;
}
cout << endl;*/
for (int j = cross_section[0]; j < cross_section[1] + 1; j++) {
X_code_tem1[1][j] = X_code_tem1[0][j];
}
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[0][j];
}
count++;
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[1][j];
}
count++;
}
else if ((per_cross[i][1] == per_copy[0]) && (per_cross[i][0] != per_copy[0])) {//有其中一个
for (int j = 0; j < node; j++) {
X_code_tem1[0][j] = X_code_tem[per_cross[i][0]][j];
X_code_tem1[1][j] = X_code_tem[per_cross[i][1]][j];
}
/*cout << endl;
for (int k = 0; k < 2; k++) {
for (int j = 0; j < node; j++) {
cout << X_code_tem1[k][j] << " ";
}
cout << endl;
}
cout << endl;*/
for (int j = cross_section[0]; j < cross_section[1] + 1; j++) {
X_code_tem1[0][j] = X_code_tem1[1][j];
}
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[0][j];
}
count++;
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[1][j];
}
count++;
}
else {//没有最佳基因
for (int j = 0; j < node; j++) {
X_code_tem1[0][j] = X_code_tem[per_cross[i][0]][j];
X_code_tem1[1][j] = X_code_tem[per_cross[i][1]][j];
}
/*cout << endl;
for (int k = 0; k < 2; k++) {
for (int j = 0; j < node; j++) {
cout << X_code_tem1[k][j] << " ";
}
cout << endl;
}
cout << endl;*/
for (int j = cross_section[0]; j < cross_section[1] + 1; j++) {
temp[j] = X_code_tem1[0][j];
}
for (int j = cross_section[0]; j < cross_section[1] + 1; j++) {
X_code_tem1[0][j] = X_code_tem1[1][j];
}
for (int j = cross_section[0]; j < cross_section[1] + 1; j++) {
X_code_tem1[1][j] = temp[j];
}
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[0][j];
}
count++;
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[1][j];
}
count++;
}
}
else {//不交叉,直接复制
for (int j = 0; j < node; j++) {
X_code_tem1[0][j] = X_code_tem[per_cross[i][0]][j];
X_code_tem1[1][j] = X_code_tem[per_cross[i][1]][j];
}
/*cout << endl;
for (int k = 0; k < 2; k++) {
for (int j = 0; j < node; j++) {
cout << X_code_tem1[k][j] << " ";
}
cout << endl;
}
cout << endl;*/
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[0][j];
}
count++;
for (int j = 0; j < node; j++) {
X_code[count][j] = X_code_tem1[1][j];
}
count++;
}
}
/*cout << "交叉个体:" << endl;
for (int i = 0; i < person_number; i++) {
for (int j = 0; j < node; j++) {
cout << X_code[i][j] << " ";
}
cout << endl;
}
cout << endl;*/
}
3.约束问题优化
对于带约束的函数优化问题,可以参照PSO算法求解的内容,使用罚函数的方法进行约束处理,转变为无约束问题求解。
此外,遗传算法的高级实现方式以及并行算法,是对求解过程的改进,与SGA方法相比,改进的方法求解速度更快,准确度更高,也能避免局部最优的发生。
以上内容,如有引用不当,将立即修改。
欢迎各位同学进行交流!