SIFT特征
参考文献:
https://www.cnblogs.com/jsxyhelu/p/7591497.html
1.SIFT概述
SIFT的全称是Scale Invariant Feature Transform,是一种具有尺度不变性和光照不变性的特征描述子,也同时是一套特征提取的理论,首次由D. G. Lowe于2004年以《Distinctive Image Features from Scale-Invariant Keypoints[J]》发表于IJCV中。开源算法库OpenCV中进行了实现、扩展和使用。SIFT特征对旋转、尺度缩放、亮度变化等保持不变性,是一种非常稳定的局部特征。
依据原始论文,SIFT算法流程分为4个部分:
1、DoG尺度空间构造(Scale-space extrema detection)
2、关键点搜索与定位(Keypoint localization)
3、方向赋值(Orientation assignment)
4、关键点描述(Keypoint descriptor)
此外再添加第5个部分,用于说明一些需要特殊说明的重要内容。类似游戏攻略的主线和分线。
2.1"尺度"简介
图像处理中的"尺度"可以理解为图像的模糊程度,类似眼睛近视的度数。尺度越大细节越少,SIFT特征希望提取所有尺度上的信息,也就是无论图像是否经过放大缩小都能够提取特征。这种思考,是和人的生理特征类似的,比如我们即使是在模糊的情况下仍然能够识别物体的种类,生理上人体对物体的识别和分类和其尺度(模糊程度)没有直接关系。
高斯函数在图像处理中得到了广泛的运用,源于其本身具有的优良特性(高斯函数的优良特性放在6.1节);在图像处理中对图像构建尺度空间的方法,是使用不同sigma值的高斯核对图像进行卷积操作(注意,sigma就是“尺度”)。
![]() 是高斯核,其数学表述为:
是高斯核,其数学表述为:
整个高斯卷积表示为:
![]()
其中![]() 是原图像,*是卷积符号,
是原图像,*是卷积符号,![]() 对应尺度下的尺度图像,这里简单了解一下,我们看一下在OpenCV中实现不同sigma的高斯卷积的代码和结果
对应尺度下的尺度图像,这里简单了解一下,我们看一下在OpenCV中实现不同sigma的高斯卷积的代码和结果
Mat matSrc = imread("e:/template/lena.jpg");
pyrDown(matSrc,matSrc);
imshow("原始图",matSrc);
Mat matDst;
GaussianBlur(matSrc,matDst,Size(0,0),1);
imshow("sigma是1",matDst);
GaussianBlur(matSrc,matDst,Size(0,0),3);
imshow("sigma是3",matDst);
GaussianBlur(matSrc,matDst,Size(0,0),5);
imshow("sigma是5",matDst);其中左上角为原图,右上角为sigma=1尺度下的图像,下行左右分别是sigma=3,sigma=5的图像,尺度越大,图像越模糊,这是直观印象。但是即使sigma=5,你也能够勉强认出这是一个人像;如果你的头脑中有lena这个模型,见过lena的图片,你就能够很快识别出这是lena的图片变模糊的结果。这就是基本上一个人脑的识别流程。“尺度”就是这些。
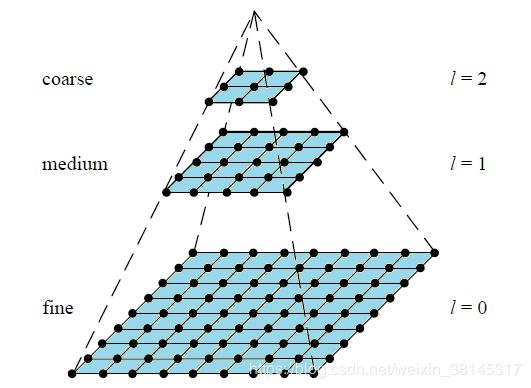
图像金字塔也是图像处理中的常用的概念,一般通过对原始图像逐步进行下(降)采样(每隔2个像素抽取一个像素)得到x和y都为原始图像1/2的缩小图像。
对于二维图像,一个传统的金字塔中,每一层图像由上一层分辨率的长、宽各一半,也就是四分之一的像素组成;注意金字塔上一个上小下大的东西,它的层数是由下向上来数的,底层叫做第0层,然后往上依次为1、2、3层。
2.3“高斯金字塔”
现在我们已经知道,金字塔就能够用来解决大小的变化;而不同尺度的gauss核用来解决模糊程度的变化。聪明的计算机工程师想到把这两者结合起来。
因为有高斯和金字塔嘛,直来直往的就叫做“高斯金字塔”吧。它的模型应该是看上去这样的:大体看上去是一个金字塔,但是每层都是“复合”结构,是有若干张不同尺度的处理结果叠加起来的。
二、关键点搜索与定位(Keypoint localization)
2.1初略寻找
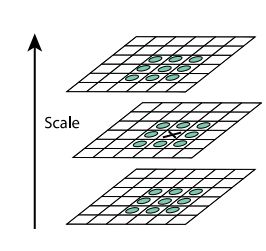
像“扫雷”游戏一样,除了边缘点外,每个点有8个相联的位置(最多有8个地雷);那么在已经建立起来的DoG空间中,除了边缘的点,每个点有9*3-1 = 26 个领域。在这个26个领域里面寻找最大最小的点,认为可能是关键点。如下图![]() 标注的点要和周围26个绿色的点比较。
标注的点要和周围26个绿色的点比较。