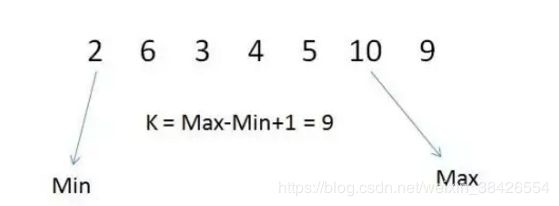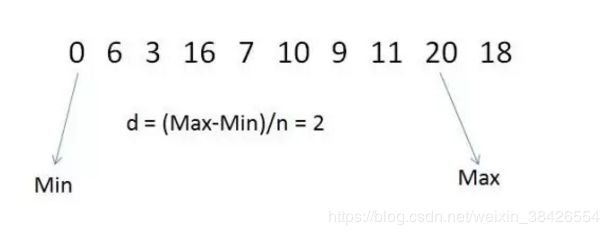LeetCode：无序数组排序后的最大相邻差

最近看了《漫画算法》这本书，小灰大神这本书写的不是一般好。受益匪浅，讲总结的知识点归纳出来。  

有一个无序整型数组，如何求出该数组排序后的任意两个相邻元素的最大差值？要求时间复杂度和空间复杂度尽可能低。（例如：无序数组 2,3,1,4,6，排序后是1,2,3,4,6，最大差值是6-4=2）

解法一： 先使用时间复杂度为O(nlogn)的排序算法给原来数组排序，然后遍历数组，对每两个相邻元素求差，最终得到最大差值。

该解法可行是可行，但不是最好的解法。

解法二：

1.利用计数排序的思想，先求出原数组的最大值Max与最小值Min的区间长度k（k=Max-Min+1）。

2.创建一个长度为k的新数组Array。

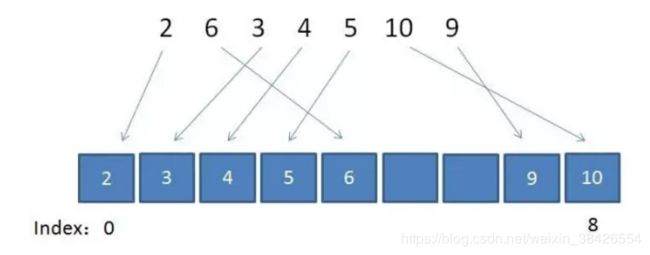
3.遍历原数组，把原数组每一个元素插入到新数组Array对应的位置，比如元素的值为n，则插入到Array[n-min]当中。此时Array的部分位置为空，部分位置填充了数值。

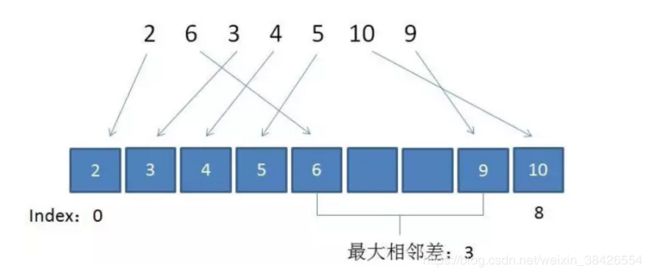
4.遍历新数组Array，统计出Array中最大连续出现空值的次数+1，即为相邻元素最大差值。

例如给定无序数组 { 2, 6, 3, 4, 5, 10, 9 }，处理过程如下图：

  

  

  

该解法的时间复杂度为O（n+k），空间复杂度同样是O（n+k）

代码：

 public static void main(String[] args) {

        int[] array = new int[] {2, 6, 3, 4, 5, 10, 3};
//        int[] array = new int[]{0, 0, 1, 2, 3, 4, 5, 6, 12, 13, 20, 10};
        Integer maxAdjustDifference = getMaxAdjustDifference(array);
        System.out.println("最大相邻差为:"+ maxAdjustDifference);
    }
/**
 *  计数排序思想： 获取无序数组的最大相邻差
 *  步骤： 
 *      1. 获取数组中的最大值和最小值，构建数组的长度
 *      2. 将数组依次放入计数排序的数组中
 *      3. 统计空值，判断0值最多连续出现的次数
 *      4. 计算最大相邻差
 * @param array
 * @return
 */
public static Integer getMaxAdjustDifference(int[] array) {
    // 1. 获取数组中的最大值和最小值，构建数组的长度
    int max = array[0];
    int min = array[0];
    for (int i = 1; i < array.length; i++) {
        if (array[i] > max) {
            max = array[i];
        }
        if (array[i] < min) {
            min = array[i];
        }
    }
    // 用来计算在统计数组中的下标
    int distance = max - min;
    int[] countArray = new int[distance+1];
    // 2. 将数组依次放入计数排序的数组中
    for (int i = 0; i < array.length; i++) {
        countArray[array[i] - min]++;
    }
    System.out.println("计数排序后的数组为："+Arrays.toString(countArray));
    int maxNearDifference = 0;
    int count = 0;
    // 最大连续数
    int maxCount = 0;
    // 连续的开始位置
    int startIndex = 0;
    // 结束的开始位置
    int endIndex  = 0;
    for (int i = 0; i < countArray.length; i++) {
        if (countArray[i] == 0) {
            if (count == 0) {
                // 记录连续为0的前一个位置
                startIndex = i-1;
            }
            // 3. 统计空值，判断0值最多连续出现的次数
            count++;
        }else {
            count = 0;
        }
        if (count > maxCount) {
            maxCount = count;
            // 记录连续为0的结束位置的后一个位置
            endIndex = i+1;
        }
    }
    // 4. 计算最大相邻差
    maxNearDifference = endIndex - startIndex;
    return maxNearDifference;
}

解法三：

1.利用桶排序的思想，先求出原数组从最小值Min到最大值Max的单位区间长度d，d=(Max-Min)/n。算出d的作用是为了后续确定各个桶的区间范围划分。

2.创建一个长度是N+1的数组Array，数组的每一个元素都是一个List，代表一个桶。

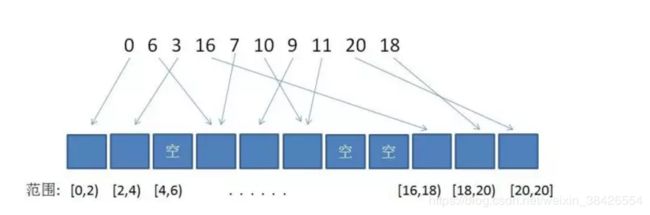
3.遍历原数组，把原数组每一个元素插入到新数组Array对应的桶当中，进入各个桶的条件是根据不同的数值区间（数值区间如何划分，看后面的图就明白了）。由于桶的总数量是N+1，所以至少有一个桶是空的。

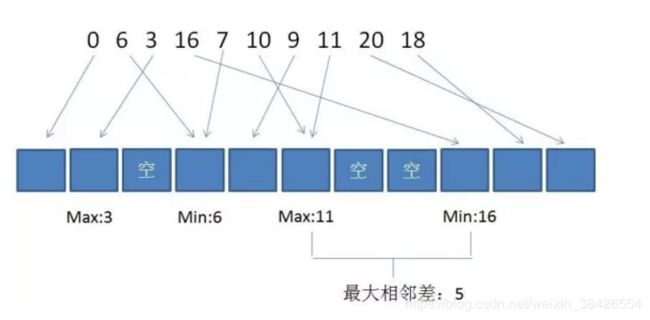
4.遍历新数组Array，计算每一个空桶右端非空桶中的最小值，与空桶左端非空桶的最大值的差，数值最大的差即为原数组排序后的相邻最大差值。

例如给定无序数组 { 0, 6, 3, 16, 7, 10, 9, 11, 20, 18 }，处理过程如下图：

该解法的时间复杂度为O（n），空间复杂度同样是O（n）。

代码：

/**
     *  桶排序思想：获取无序数组的最大相邻差
     *  步骤：
     *      1. 获取数组中的最大值和最小值，构建数组的长度
     *      2. 初始化桶
     *      3. 遍历原始数组，确定每个桶的最大最小值
     *      4. 遍历桶，找到最大差值
     * @param array
     * @return
     */
    public static int getMaxSortedDistance(int[] array) {
        // 1. 获取数组中的最大值和最小值，构建数组的长度
        int max = array[0];
        int min = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if (array[i] < min) {
                min = array[i];
            }
        }
        int distance = max - min;
        // 如果max和min相等，说明数组所有元素都相等，返回0
        if (distance == 0) {
            return 0;
        }
        // 2. 初始化桶
        int bucketNum = array.length;
        Bucket[] buckets = new Bucket[bucketNum];
        for (int i = 0; i < bucketNum; i++) {
            buckets[i] = new Bucket();
        }

        // 3. 遍历原始数组，确定每个桶的最大最小值
        for (int i = 0; i < array.length; i++) {
            // 确定数组元素所属的桶小标
            int index = ((array[i] - min) * (bucketNum - 1)) / distance;
            if (buckets[index].min == null || buckets[index].min > array[i]) {
                buckets[index].min = array[i];
            }
            if (buckets[index].max == null || buckets[index].max < array[i]) {
                buckets[index].max = array[i];
            }
        }

        // 4. 遍历桶，找到最大差值
        // 这里采用临时变量leftMax,在每一轮迭代时存储当前左侧桶的最大值，
        // 而两个桶之间的差值，则是buckets[i].min - leftIndex
        int leftIndex = buckets[0].max;
        int maxDistance = 0;
        for (int i = 1; i < buckets.length; i++) {
            if (buckets[i].min == null) {
                continue;
            }
            if (buckets[i].min - leftIndex > maxDistance) {
                maxDistance = buckets[i].min - leftIndex;
            }
            leftIndex = buckets[i].max;
        }
        return maxDistance;

    }

    /**
     * 桶
     */
    private static class Bucket{
        Integer min;
        Integer max;
    }

public static void main(String[] args) {

        int[] array = new int[] {2, 6, 3, 4, 5, 10, 3};
//        int[] array = new int[]{0, 0, 1, 2, 3, 4, 5, 6, 12, 13, 20, 10};
        // 桶排序方式
        int maxSortedDistance = getMaxSortedDistance(array);
        System.out.println("最大相邻差为:"+ maxSortedDistance);

    }