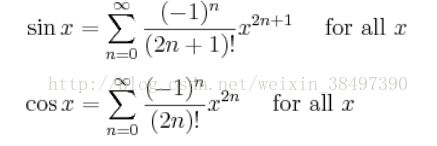C/C++实现三角函数的方法
前几天在超算学堂上用C语言做一个并行计算求函数积分的作业,恰好平台不支持math.h头文件,于是自己设计了两种计算三角函数的方法,在这里进行总结。
首先最容易想到的是利用泰勒展开式:
注意泰勒展开式的分母部分,要知道int的最大值为2147483647 < 13!,所以当n=6时就要结束累和,而此时由于泰勒展开式的收敛速度并不快,所以误差仍然很大(当x=8时,利用泰勒展开式实现的sinx与math库中自带sinx的绝对误差已经超过了200),因此不能使用泰勒展开式来实现三角函数。
在这里介绍一种相对精确度好很多的实现三角函数的方法——利用CORDIC算法,关于CORDIC算法的介绍详见这篇博客:http://blog.csdn.net/liyuanbhu/article/details/8458769
在这里以求sin(x)为例,主要利用的是直角坐标旋转的公式:
x' = cos(θ)*x - sin(θ)*y
y' = sin(θ)*x + cos(θ)*y
主要思路如下:给定一个弧度值a,函数从0开始,首先正向旋转π/4,直到旋转后的弧度值超过a,此时退回π/4,在继续正向旋转π/8,直到弧度值超过a,再退回π/8,再正向旋转π/16。。。如此循环直到旋转的弧度与a的误差小于一定值(下面代码中取π/16384),之后利用此时的x坐标和y坐标来计算出sin
算法的思路类似与二分查找,在实现算法时只需要知道特定几个弧度的三角函数值,就可以求出其它任意弧度的三角函数值,不存在溢出的问题,并且理论上精确度可以达到浮点数绝对值的最小值(精确度靠最终旋转弧度与a的误差和特定角度三角函数值的精确度决定)
由于最终我们要的只是坐标的比例,而不是精确的值,所以还可以上面的公式简化为(各项除以cos(θ)):
x' = x - tan(θ)*y
y' = tan(θ)*x + y
这样只需要知道特定角度的tan值就可以了,代码如下:
double pi = 3.1415926535897932;
double angle[] = {pi/4,pi/8,pi/16,
pi/32,pi/64,pi/128,
pi/256,pi/512,pi/1024,
pi/2048,pi/4096,pi/8192,pi/16384};
double tang[]={1,0.4142135623731,0.19891236737966,
0.098491403357164,0.049126849769467,
0.024548622108925,0.012272462379566,
0.0061360001576234,0.0030679712014227,
0.0015339819910887,0.00076699054434309,
0.00038349521577144,0.00019174760083571};
double sinx(double a){
if(a <= (pi/16384)){
return a; //因为a的值太小,sin a 约等于 a
}else{
//开始 CORDIC 算法
bool negitive = a < 0; // sin(-a) = -sin(a)
double x = 10;
double y = 0;
double theta = 0;
for(int i = 0;i < 13;i ++){ //开始迭代
double orix,oriy;
while(theta < a){ //当前角度小于a
orix = x;
oriy = y;
//坐标旋转
x = orix - tang[i] * oriy;
y = tang[i] * orix + oriy;
theta += angle[i];
}
if(theta == a){
if(negitive){
return -(y/sqrt((x*x+y*y)));
}else{
return (y/sqrt((x*x+y*y)));
}
}else{
//旋转的弧度超过了a,退回原来增加的角度,同时进入下一次迭代
theta -= angle[i];
x = orix;
y = oriy;
}
}
if(negitive){
return -(y/sqrt((x*x+y*y)));
}else{
return (y/sqrt((x*x+y*y)));
}
}
}参考链接:
CORDIC算法入门:http://blog.csdn.net/liyuanbhu/article/details/8458769
CORDIC_百度百科:https://baike.baidu.com/item/CORDIC