CNN模型复杂度(FLOPS、MAC)、参数量与运行速度
文章目录
- 0. 模型复杂度简介
- 1. 模型复杂度之一:模型参数量的计算方法
- 卷积层参数量计算
- 全连接层参数量计算
- 2. 模型复杂度之二:模型计算量的计算方法
- 2.1 FLOPs
- 2.1.1 注意FLOPs与FLOPS的区别
- 2.1.2 卷积层FLOPs的计算
- 2.1.3 全连接层FLOPs的计算
- 2.2 MAC、MACC、MADD
- 2.2.1 MACC概念及其与FLOPs的关系
- 2.2.2 全连接层MACC计算
- 2.2.3 激活层不计算MACC,计算FLOPs
- 2.2.3 卷积层MACC
- 2.2.4 深度可分离卷积MACC计算
- 2.2.5 批归一化
- 2.2.6 其他
- 2.3 计算公式小结
- 2.3.1 公式小结
- 2.3.2 模型计算量计算实例
- 模型计算量的应用实例
- 3. 模型复杂度之三:内存开销
- 参考
0. 模型复杂度简介
描述一个具体的深度学习模型,除了性能指标(分类任务的准确度、检测任务的mAP等),还需要考虑该模型的复杂度,即参数(Parameters,使用Mb作为单位)的个数和(前向推理的)计算量(使用FLOPs(FLoating point OPerations)或MAC(Memory Access Cost)衡量),前者描述了这个复杂的网络到底需要多少参数才能定义它?即存储该模型所需的存储空间。后者描述了数据过一遍这么复杂的网络需要多大的计算量呢?即使用该模型时所需的计算力。
1. 模型复杂度之一:模型参数量的计算方法
卷积层参数量计算
CNN卷积层的parameters分为两种: W W W和 b b b,注意这里W是大写,表示一个矩阵,也因此它相比b,既含有更多的信息,同时也是parameters的主要部分。
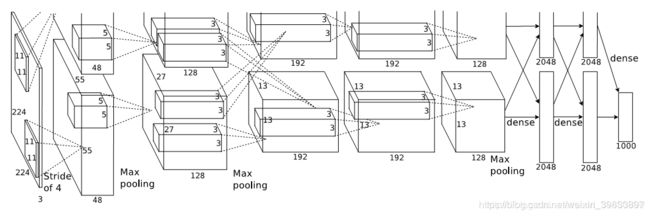
如上图所示:以经典的AlexNet模型结构为例,每个大长方体中的小长方体就是 W W W,它是大小为 [ K h , K w , C i n ] [K_h, K_w, C_{in}] [Kh,Kw,Cin]的三维矩阵,其中 K h K_h Kh表示卷积核(filter或kernel)的高度, K w K_w Kw表示卷积核的宽度, C i n C_{in} Cin表示前一级输入通道数(Channels),一般情况下, K h K_h Kh和 K w K_w Kw的大小相同,且一般都选择为3、5、7。
一个卷积核在前级特征图上从左往右、从上往下扫一遍,便会计算出很多个前向传播的值,这些值就会按原来相对位置拼成一个新的feature map,高度和宽度分别为 H o u t H_{out} Hout和 W o u t W_{out} Wout,当然一个卷积核提取的信息太过有限,于是我们需要个不同的卷积核各扫数据,于是会产生 N N N个feature map,即当前层的输出通道数 C o u t = N C_{out} = N Cout=N。
总结起来即为:尺寸为 [ K h , K w , C i n ] [K_h, K_w, C_{in}] [Kh,Kw,Cin]小长方体(当前层的滤波器组)划过前一级尺寸为 [ H i n , W i n , C i n ] [H_{in},W_{in},C_{in}] [Hin,Win,Cin]的大长方体(当前层输入的特征图)最终生成一个新的尺寸为 [ H o u t , W o u t , C o u t ] [H_{out},W_{out},C_{out}] [Hout,Wout,Cout]的大长方体(当前层输出的特征图),这一过程如下图所示。
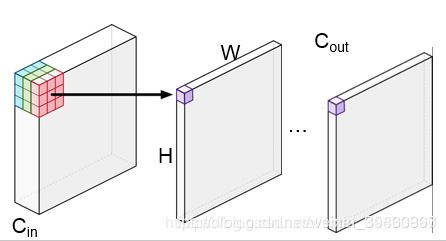
于是我们可以总结出规律:对于某一个卷积层,它的parameters个数,即 W W W和 b b b的权值个数之和为: ( K h ∗ K w ∗ C i n ) ∗ C o u t + C o u t (K_h * K_w * C_{in}) * C_{out} + C_{out} (Kh∗Kw∗Cin)∗Cout+Cout,符号定义同上文。
全连接层参数量计算
刚才讲的都是对于卷积层的,对于全连接层,比如AlexNet的后三层,其实要更简单,因为这实际是两组一维数据之间(如果是卷积层过度到全连接层,如上图第5层到第6层,会先将第5层三维数据flatten为一维,注意元素总个数未变)的两两连接相乘,然后加上一个偏置即可。所以我们也可以总结出规律:对于某个全连接层,如果输入的数据有 N i n N_{in} Nin个节点,输出的数据有 N o u t N_{out} Nout个节点,它的parameters个数为: N i n ∗ N o u t + N o u t N_{in}*N_{out}+N_{out} Nin∗Nout+Nout。如果上层是卷积层, N i n N_{in} Nin就是上层的输出三维矩阵元素个数,即 N i n = H i n ∗ W i n ∗ C i n N_{in} = H_{in}*W_{in}*C_{in} Nin=Hin∗Win∗Cin。
2. 模型复杂度之二:模型计算量的计算方法
模型的计算量直接决定模型的运行速度,常用的计算量统计指标是浮点运算数FLOPs, 对FLOPs指标的改进指标包括乘加运算 MACCs(multiply-accumulate operations),又被称为MADDs.
2.1 FLOPs
2.1.1 注意FLOPs与FLOPS的区别
FLOPs:注意s小写,是FLoating point OPerations的缩写(s表复数),意指浮点运算数,理解为计算量。可以用来衡量模型的复杂度。针对神经网络模型的复杂度评价,应指的是FLOPs,而非FLOPS。
FLOPS:注意全大写,是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度。是一个衡量硬件性能的指标。比如nvidia官网上列举各个显卡的算力(Compute Capability)用的就是这个指标,如下图,不过图中是TeraFLOPS,前缀Tera表示量级:MM,2^12之意。

2.1.2 卷积层FLOPs的计算
深度学习论文中常使用的单位是GFLOPs,1 GFLOPs = 10^9 FLOPs,即:10亿次浮点运算(10亿00百万,000千,000)
这里的浮点运算主要就是 W W W相关的乘法,以及 b b b相关的加法,每一个 W W W对应 W W W中元素个数个乘法,每一个 b b b对应一个加法,因此好像FLOPs个数和parameters是相同的。但其实有一个地方我们忽略了,那就是每一层feature map上的值是通过同一个滤波器处理的结果(权值共享),这是CNN的一个重要特性(极大地减小了参数量)。所以我们在计算FLOPs是只需在parameters的基础上再乘以feature map的大小即可,即对于某个卷积层,它的FLOPs数量为: [ ( K h ∗ K w ) ∗ C i n + 1 ] ∗ [ ( H o u t ∗ W o u t ) ∗ C o u t ] = [ ( K h ∗ K w ∗ C i n ) ∗ C o u t + C o u t ] ∗ [ H o u t ∗ W o u t ] = n u m p a r a m e t e r ∗ s i z e o u t p u t f e a t u r e m a p [(K_h * K_w )* C_{in} + 1]*[(H_{out}*W_{out})* C_{out} ] = [(K_h * K_w * C_{in}) * C_{out} + C_{out}]*[H_{out}*W_{out}]= num_{parameter}*size_{output feature map} [(Kh∗Kw)∗Cin+1]∗[(Hout∗Wout)∗Cout]=[(Kh∗Kw∗Cin)∗Cout+Cout]∗[Hout∗Wout]=numparameter∗sizeoutputfeaturemap,其中 n u m p a r a m e t e r num_{parameter} numparameter表示该层参数的数目, s i z e o u t p u t f e a t u r e m a p size_{output feature map} sizeoutputfeaturemap表示输出特征图的二维尺寸。
2.1.3 全连接层FLOPs的计算
注意:对于全连接层,由于不存在权值共享,它的FLOPs数目即是该层参数数目: N i n ∗ N o u t + N o u t N_{in} * N_{out} + N_{out} Nin∗Nout+Nout。
2.2 MAC、MACC、MADD
2.2.1 MACC概念及其与FLOPs的关系
为什么使用乘加运算指标呢?因为神经网络运算中乘加运算无处不在:
对于一个3*3滤波器在特征图上的一次运算可以表示为:
y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[n8]*x[8]
对于上式,记w[0]*x[0] +… 为一次乘加,即1MACC。所以对于上式而言共有9次乘加,即9MACCs(实际上,9次相乘、9-1次相加,但为了方便统计,将计算量近似记为9MACCs,就像算法复杂度通常表示成 O ( N ) O^{(N)} O(N)一样,都只是一种近似,不需要纠结)
MACC vs FLOPs:对于上式而言,可以认为执行了9次乘法、9-1次加法,所以一共是9+(9-1)次FLOPs。所以近似来看1MACC ≈ \approx ≈ 2FLOPs。(需要指出的是,现有很多硬件都将乘加运算作为一个单独的指令)。
2.2.2 全连接层MACC计算
In a fully-connected layer, all the inputs are connected to all the outputs. For a layer with I input values and J output values, its weights W can be stored in an I × J matrix. The computation performed by a fully-connected layer is:
y = matmul(x, W) + b
Here, x is a vector of I input values, W is the I × J matrix containing the layer’s weights, and b is a vector of J bias values that get added as well. The result y contains the output values computed by the layer and is also a vector of size J.
To compute the number of MACCs, we look at where the dot products happen. For a fully-connected layer that is in the matrix multiplication matmul(x, W).
A matrix multiply is simply a whole bunch of dot products. Each dot product is between the input x and one column in the matrix W. Both have I elements and therefore this counts as I MACCs. We have to compute J of these dot products, and so the total number of MACCs is I × J, the same size as the weight matrix.
The bias b doesn’t really affect the number of MACCs. Recall that a dot product has one less addition than multiplication anyway, so adding this bias value simply gets absorbed in that final multiply-accumulate.
Example: a fully-connected layer with 300 input neurons and 100 output neurons performs 300 × 100 = 30,000 MACCs.
| Note |
|---|
| Sometimes the formula for the fully-connected layer is written without an explicit bias value. In that case, the bias vector is added as a row to the weight matrix to make it (I + 1) × J, but that’s really more of a mathematical simplification — I don’t think the operation is ever implemented like that in real software. In any case, it would only add J extra multiplications, so the number of MACCs wouldn’t be greatly affected anyway. Remember it’s an approximation. |
In general, multiplying a vector of length I with an I × J matrix to get a vector of length J, takes I × J MACCs or (2I - 1) × J FLOPS.
If the fully-connected layer directly follows a convolutional layer, its input size may not be specified as a single vector length I but perhaps as a feature map with a shape such as (512, 7, 7). Some packages like Keras require you to “flatten” this input into a vector first, so that I = 512×7×7. But the math doesn’t change.
| Note: |
|---|
| In all these calculations I’m assuming a batch size of 1. If you want to know the number of MACCs for a larger batch size B, then simply multiply the result by B. |
2.2.3 激活层不计算MACC,计算FLOPs
Usually a layer is followed by a non-linear activation function, such as a ReLU or a sigmoid. Naturally, it takes time to compute these activation functions. We don’t measure these in MACCs but in FLOPS, because they’re not dot products.
Some activation functions are more difficult to compute than others. For example, a ReLU is just:
y = max(x, 0)
This is a single operation on the GPU. The activation function is only applied to the output of the layer. On a fully-connected layer with J output neurons, the ReLU uses J of these computations, so let’s call this J FLOPS.
A sigmoid activation is more costly, since it involves taking an exponent:
y = 1 / (1 + exp(-x))
When calculating FLOPS we usually count addition, subtraction, multiplication, division, exponentiation, square root, etc as a single FLOP. Since there are four distinct operations in the sigmoid function, this would count as 4 FLOPS per output or J × 4 FLOPS for the total layer output.
It’s actually common to not count these operations, as they only take up a small fraction of the overall time. We’re mostly interested in the (big) matrix multiplies and dot products, and we’ll simply assume that the activation function is free.
In conclusion: activation functions, don’t worry about them.
2.2.3 卷积层MACC
The input and output to convolutional layers are not vectors but three-dimensional feature maps of size H × W × C where H is the height of the feature map, W the width, and C the number of channels at each location.
Most convolutional layers used today have square kernels. For a conv layer with kernel size K, the number of MACCs is:
K × K × Cin × Hout × Wout × Cout
Here’s where that formula comes from:
- for each pixel in the output feature map of size Hout × Wout,
- take a dot product of the weights and a K × K window of input values
- we do this across all input channels, Cin
- and because the layer has Cout different convolution kernels, we repeat this Cout times to create all the output channels.
Again, we’re conveniently ignoring the bias and the activation function here.
Something we should not ignore is the stride of the layer, as well as any dilation factors, padding, etc. That’s why we look at the dimensions of the layer’s output feature map, Hout × Wout, since that already has the stride etc accounted for.
Example: for a 3×3 convolution with 128 filters, on a 112×112 input feature map with 64 channels, we perform this many MACCs:
3 × 3 × 64 × 112 × 112 × 128 = 924,844,032
That’s almost 1 billion multiply-accumulate operations! Gotta keep that GPU busy…
| Note: |
|---|
| In this example, we used “same” padding and stride = 1, so that the output feature map has the same size as the input feature map. It’s also common to see convolutional layers use stride = 2, which would have chopped the output feature map size in half, and we would’ve used 56 × 56 instead of 112 × 112 in the above calculation. |
2.2.4 深度可分离卷积MACC计算
2.2.5 批归一化
2.2.6 其他
2.3 计算公式小结
2.3.1 公式小结
计算公式小结如下:

关于FLOPs的计算,Nvidia的Pavlo Molchanov等人的文章的APPENDIX中也做了介绍,

由于是否考虑biases,以及是否一个MAC算两个operations等因素,最终的数字上也存在一些差异。但总的来说,计算FLOPs其实也是在对比之下才显示出某种算法,或者说网络的优势,所以必须在同一组计算标准下,才是可以参考的、有意义的计算结果。
2.3.2 模型计算量计算实例
采用1、2两节的方法,可以很轻松地计算出AlexNet网络的parameters和FLOPs数目,如下图

模型计算量的应用实例
3. 模型复杂度之三:内存开销
参考
主要参考:
https://machinethink.net/blog/how-fast-is-my-model/
上篇:https://www.jiqizhixin.com/articles/2019-02-22-22
下篇:https://www.jiqizhixin.com/articles/2019-02-28-3
上篇:https://www.leiphone.com/news/201902/D2Mkv61w9IPq9qGh.html
下篇:https://www.leiphone.com/news/201902/biIqSBpehsaXFwpN.html?uniqueCode=OTEsp9649VqJfUcO
关于网络轻量化:https://www.jianshu.com/p/b4e820096ace
工具:
https://github.com/sovrasov/flops-counter.pytorch
