Coursera 斯坦福吴恩达机器学习课程笔记 (1)
看了课程一周后发现忘光了,决定做一个笔记用作复习。如果涉及到侵权问题请联系我,我会立马删除并道歉。
同时,禁止任何形式的转载,包括全文转载和部分转载。如需使用请联系本人 [email protected]。如若发现侵权行为,我学过知识产权法的,嘿嘿
第一周:基础概念和介绍
对机器学习的理解
机器学习现在也没有统一的定义。最浅显易懂的就是赋予计算机不需要得到清晰完整代码就能够通过“自我学习”来完成任务的能力(Arthur Samuel 1959)。这样说依然很抽象,还有一个浅显的例子就是对于一个computer program, 对于给定任务T,这个程序可以通过某些experience E, 使用恰当的measurements P来学习T,并最终达到提高P的效果。
举个例子:
(1)下棋,观看用户下棋就是E,赢得游戏就是T,赢得游戏的时间(或其他衡量)就是P。机器要通过E来完成T任务,并且不断提高P。
(2)spam. 观看用户给邮件贴label(尤其是垃圾邮件)是E,分类垃圾邮件是E,成功分类是P
机器学习算法:
supervised learning
对于output我们有清楚的认知,我们想要什么样的结果(对于input我们有足够的label来标记我们的数据)。比如预测澳大利亚十年后兔子的数量,我们很清楚这会是一个具体的数值。
常见的有回归问题、分类问题(注意分类问题可以有不止0,1两类,例子包括肿瘤预测等)
unsupervised learning
对于input我们是没有label的,我们并不知道这些数据可以被分为多少类。例如给100篇文章分类,我们并不知道他们可以分成多少类,唯一可以做到的是将关键词等类似的文章分为一类。还有的例子包括基因测序等。
cocktail party problem
party中有两个话筒,一个用于讲话,一个用于收音(BGM)。如何使用电脑将人声和BGM分离呢?就可用到无监督学习。
线性回归
我们将数据分为两类:训练集和验证集
训练集用于训练模型,使用特定的criteria (e.g. cv等)来选定模型。验证集用于验证训练的模型的有效度。
cost function
cost function 是fitted-observed之间差值的距离,优化模型就是通过最小化cost function完成的
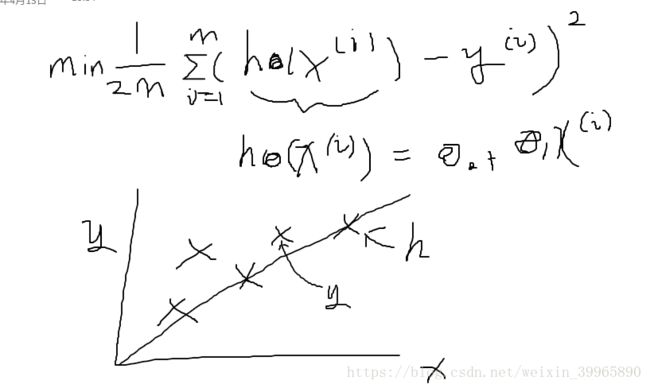
m 为训练集数据个数,平方和是为了消除差之间的互相抵消。
下式写作J(θ0,θ1),叫做squared error function, 这是最常见的回归问题的cost function。
例子:对于简单一元线性回归 y = θ0+θ1x, J(0)就是y = 0
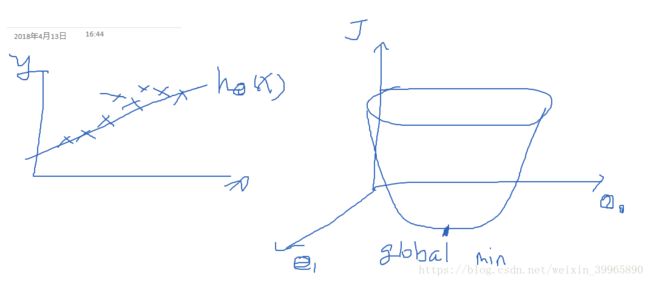
对于简单一元线性回归,左边是模型hθ(x), 右边是cost function J(θ0,θ1)。 我们可以清楚看见J的全局最小值(即h的全局最优解)是出现在这个钟形函数的底部的。通过确定此时的θ0和θ1,我们就能确定最优的hθ(x)。
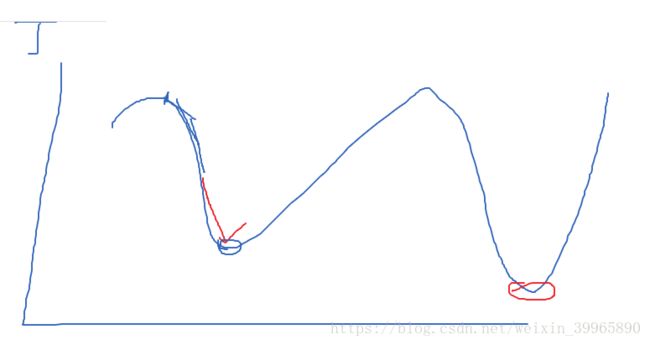
注意:因为简单一元线性回归的特性,J的全局最小值就等于其局部最小值,这是特殊的。通常我们只能求得J的局部最小值。如下图,很明显右边的点是全局全局最小值,但是我们是从左边的点的上方开始建模的,一般只能求得左边的局部最优解。这个问题在神经网络里尤为突出,因为神经网络的start point是随机的,所以很可能无法达到全局最优解。
Gradient descent (不止用于线性回归)
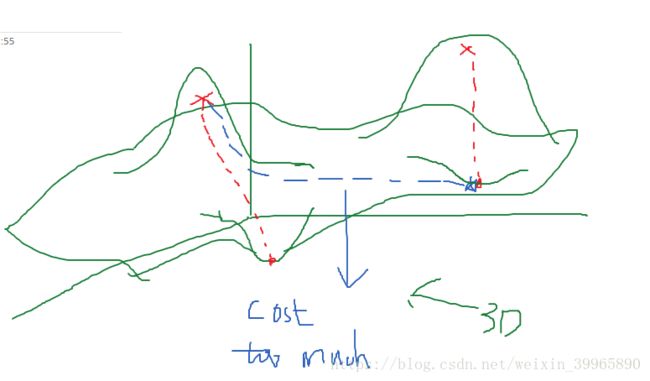
gradient descent是寻求最优解的一个常用方法。这里有一个大前提:在gradient descent找到一个最优解之后,它就会停下,不会马不停蹄给你找下一个更好的解。谁一天那么闲没事天天给你找解啊,程序也是有脾气的,哼。这个算法相当于一个下坡的过程,如果我一开始站在左边的山头上,向着红色线的方向下坡(一般此过程为求导后从原位置减去求导量和learning rate的乘积(公式见下下图),这里的learning rate就可以理解为我一步跨多大),最终达到左边的全局最优解(我假设他是最优解);如果我一开始站在右侧的山头,顺着红线下坡,很有可能就会到达右侧的局部最优解;同样的,如果从左边的山头顺着蓝线下坡,也是有可能会到达右边的局部最优解的,全看我走的方向如何。当然,显而易见这样需要的成本更大。同理,如果我一开始站在右边山头想走到左边的全局最优解,成本依然很大。
这几个宛如狗爬的字是: repeat until convergence
α即上段提到的learning rate,α的值一定要取的适当。如果α太小,我下山的步子太小,就会浪费很多资源来获取局部最优解。如果α太大,我下山步子太大(嗯。。。一脚跨过一座山哈哈哈哈),我可能会略过局部最优解,如果还有局部最优解那还好,可是对于二次的cost function,我可能就会错过唯一的最优解然后获得越来越大的误差。
注意这里的:=和=符号的区别,:=是assignment, a:= a+1就是让a+1; = 是既成事实,a=a+1就是不对的,永远不可能发生。(这里应该就类似于编程语言的==和=)
注意:这里θ0和θ1应该是simultaneously update的,即,要找优化解我们应该同时计算两者的值,而不是计算其中一个,将这个参数的最优解套入下一个参数的计算得到下一个参数的最优解
【上图是现抄课件,本人无版权,感谢coursera, 斯坦福和吴恩达爸爸,侵删】
Batch
“Each step of gradient descent uses all the training examples” ——摘自coursera machine learning Andrew Ng课件,侵删
第二周 多元线性回归
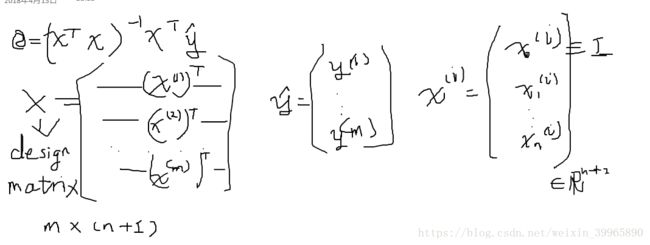
如果要把model写成hθ(x)=θ^TX的话,x0=1
Feature Scaling
目的是为了(1)让covariate之间的权重更加平衡,例如一组数据,工资的范围是2000-10000,年龄的范围只是20-30,在建模时很容易工资的权重就大大影响了模型,而实际上年龄才是主要的covariate。此外,当我们使用二次甚至更高次模型的时候,feature scaling就变得更重要了(2)让gradient descent更快找到收敛的位置。如下图,对于范围差距很大的数据,形成的cost function很可能是A这种奇形怪状的,不利于寻找局部最优解。如果我们将数据处理到等量级或相似量级,cost function就越接近B——一个圆形,就方便找很多了。
那么什么是好的feature scaling呢? 这个范围也不是越小、越精确越好,我们依然需要给feature一定的空间:[-1,1]就是一个合理的范围,[-0.001,0.001]就有点太过了,同理[-100,100]也有点不合适。当然,这个范围不需要对称。
Mean Normalisation
用x-mean替代x,对x0=1无效。
P.S. 吴恩达爸爸好帅啊,声音好温柔~~~~花痴一下
确保gradient descent正确运行
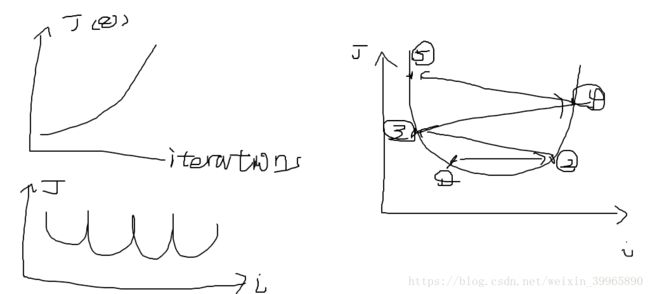
(1)可以画一个J(θ)最小值X迭代次数的图,J(θ)应该是单调递减并在某处收敛的。我们可以通过判断函数来判断α是大了呢,还是小了呢,是饿了呢,还是渴了呢。通常阿尔法取值在[0.001,1]之间,尽可能多试试,通过图形来分析哪个α更合适
(2)automatic convergence test: 当J(θ)减少的量小于一个threshold 艺圃C龙(音译,那个希腊字母,懒得打了)时,停止迭代。但是通常找一个合适的threshold是很难滴,所以恩达更愿意看图
例子:
对于下图左边两种情况,很可能是α太大了,一次跨的幅度太大
Normal Equation (思想应该是同statistical learning的GLS)
Octave: pinv() = inverse X' == x transfer
对于normal equation, feature scaling是不必要的
但是如果X^TX是不可逆的呢(singular/degenerate)?
(1) 造成不可逆的原因(这同时也是我们检查原因的顺序):
a. features高度相关,比如x和x^2
b. features过多,比如features的数量已经多于数据的量了(这种情况我在学习中还没遇到过,应该是很少见的),
i. 这里可以删掉一些features,
ii. 或者use regularization(之后会讲到)
Gradient Descent vs. Normal Equation
| Gradient Descent | Normal Equation |
| 需要选择α | 不需要选择α |
| 需要多次迭代 | 计算一次到位 |
当n很大的时候 also works well [当features太多 (>=10000),吴恩达的选择] |
需要计算(X^TX)^-1 |
| 当n很大,收敛很慢 | |
| 适用范围更广 | 对linear regression效果很好 |
——n为features的数量,不是数据的数量(m)
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------代码部分------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Octave command line
a = 3; %semicolon supressing output 不显示输出结果
~= 为不等号
xor(1,0)或门
c = (3>=1);
c =1 (True)
pi = π
a = pi 结果: a = 3.1416
a = pi; 结果:无输出
Octave 的print 很像C语言:
disp(sprintf('2 decimals: %0.2f', a)) 结果:2 decimals: 3.14
format long/short 显示不同位数
A[1 2; 3 4; 5 6] 注意用空格而不是逗号
v = 1:0.1:2 生成一个从1-2的差值为0.1的 11*1矩阵(第一二列都是1)
ones(2,3) 生成一个2*3的全为1的矩阵
zeros() 同理
rand(1,3)随机数(不过我觉得应该不是完全随机的,还是有seed的)
randn(2,3) 生成正态分布矩阵
sqrt(10)*randn(1,1000)就相当于R的rnorm(1000,sqrt(10))了
eye(4) 生成一个4*4的元矩阵
help eye 出解释
size(Matrix) 返回结果是一个[行 列]的 1*2矩阵
length(Matrix/Vector) 返回行数
pwd显示当前路径
常见命令与linux同
load featuresX,dat = load('featuresX.dat')
who 显示当前环境下的变量
whos 给出detail
clear featuresX 清除
save hello.mat v; 将变量v存放入环境hello.mat
save hello.txt v -ascii 将该文件以ASCII形式存储
A(2,3)第二行第三列
A(2,:)第二行
A(:,2)第二列
:与R的space同
A .*B 是A矩阵和B矩阵的每个element各自相乘(前提是AB矩阵维度相同)
A .^2 是A矩阵每个element各自平方(看来.?是用于矩阵element的专门的操作)
A' 转置
pinv(A) 逆矩阵
[val, ind] = max(a) 找出向量a中的最大值并给出其index
max(A) 会给出每一列中的最大值 = max(A,[],1) 每列最大值
max(A,[],2) 每行最大值
这里类似R用1表示列,2表示行
a = [1 15 2 0.5]
a <3
ans = 1 0 1 1
find(a <3)
ans = 1 3 4
A .* eye(9) 出去从左到右对角线保留,其余值全部为0
plot(x,y, 'r')——r 为红色
xlabel('') ylabel('') legend('','') title('')
这里能分别添加我觉得Octave是将这些变量全部存储然后保持运行
print -dpng 'myplot.png'存储
figure(1): plot(t,y1); 赋值,打开新窗口
clf; 清除所有figure
subplot(1,2,1); 把plot分割成1:2 grid, 获取第一个element
subplot(1,2,2);
——这两步合起来相当于 par(mfrow=c(1,2))
for i = 1:10,
v(i) = 2^i;
end;
while i <=5,
v(i) =100;
i = i+1;
end;
while true,
v(i) =999;
i = i+1;
if(i>10|| i ==10),
beark;
end;
end; 注意两个end
addpath('') 添加路径,这样不在此路径下也可以使用function
Vectorization (能使代码运行快得多)
将连乘、连加等形式转化为矩阵的思维
比如
正常我会用for循环把它挨个加起来,这里其实用矩阵能更方便解决这个问题
cost function也可以这样处理