DL优化函数之mini-batch SGD
SGD随机梯度下降法对经典的梯度下降法有了极大速度的提升。但有一个问题就是由于过于自由 导致训练的loss波动很大。那么如何可以兼顾经典GD的稳定下降同时又保有SGD的随机特性呢?于是小批量梯度下降法, mini-batch gradient descent 便被提了出来。其主要思想就是每次只拿总训练集的一小部分来训练,比如一共有5000个样本,每次拿100个样本来计算loss,更新参数。50次后完成整个样本集的训练,为一轮(epoch)。由于每次更新用了多个样本来计算loss,就使得loss的计算和参数的更新更加具有代表性。不像原始SGD很容易被某一个样本给带偏 。loss的下降更加稳定,同时小批量的计算,也减少了计算资源的占用。SGD 是无论学术圈写文章做实验还是工业界调参跑模型最常用的模型优化算法,但是有时候容易被忽略的一点是:一般提到的 SGD 是指的 Mini-batch SGD,而非原教旨意义下的单实例 SGD。其训练过程如下图所示:
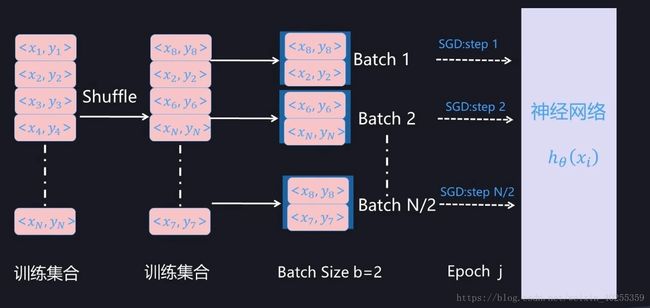
Mini-Batch」, 是指的从训练数据全集 T 中随机选择的一个训练数据子集合。假设训练数据集合 T 包含 N 个样本,而每个 Mini-Batch 的 Batch Size 为 b,于是整个训练数据可被分成 N/b 个 Mini-Batch。在模型通过 SGD 进行训练时,一般跑完一个 Mini-Batch 的实例,叫做完成训练的一步(step), 跑完 N/b 步则整个训练数据完成一轮训练,则称为完成一个 Epoch。完成一个 Epoch 训练过程后,对训练数据做随机 Shuffle 打乱训练数据顺序,重复上述步骤,然后开始下一个 Epoch 的训练,对模型完整充分的训练由多轮 Epoch 构成。
拿到一个 Mini-Batch 进行参数更新时,首先根据当前 Mini-Batch 内的 b 个训练实例以及参数对应的损失函数的偏导数来进行计算,以获得参数更新的梯度方向,然后根据 SGD 算法进行参数更新,以此来达到本步(Step)更新模型参数并逐步寻优的过程。其训练过程如下图所示:

如果机器学习任务的损失函数是平方损失函数:
由 Mini-Batch 内训练实例可得出 SGD 优化所需的梯度方向为:
其中,是 Mini-Batch 内第 i 个训练实例对应的输入 。是希望学习到的映射函数,其中θ是函数对应的当前参数值。代表了 Mini-Batch 中实例i决定的梯度方向,Batch 内所有训练实例共同决定了本次参数更新的梯度方向。
根据梯度方向即可利用标准 SGD 来更新模型参数:
对于 Mini-Batch SGD 训练方法来说,为了能够参数更新必须得先求出梯度方向,而为了能够求出梯度方向,需要对每个实例得出当前参数下映射函数的预测值,这意味着如果是用神经网络来学习映射函数的话,Mini-Batch 内的每个实例需要走一遍当前的网络,产生当前参数下神经网络的预测值。
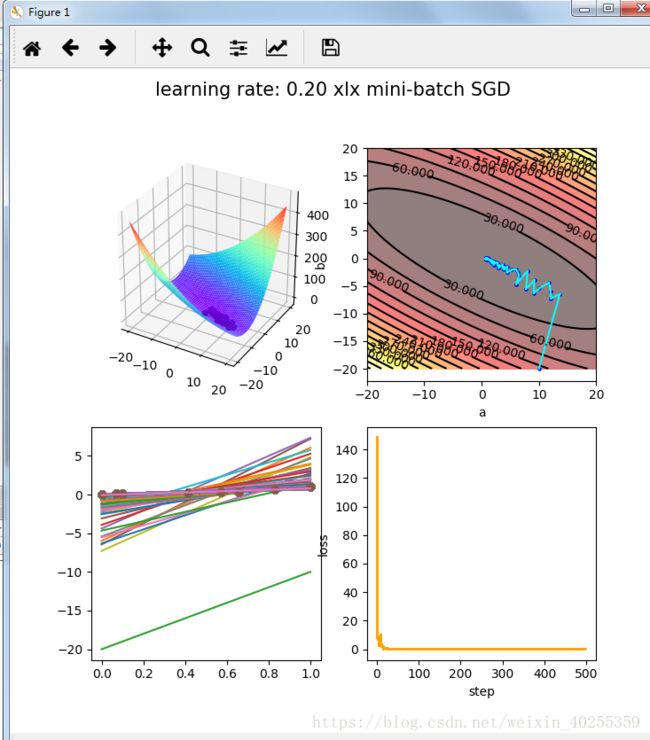
用一个python代码例子实现如下:学习率为0.2
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
rate = 0.2 # learning rate
def da(y,y_p,x):
return (y-y_p)*(-x)
def db(y,y_p):
return (y-y_p)*(-1)
def calc_loss(a,b,x,y):
tmp = y - (a * x + b)
tmp = tmp ** 2
SSE = sum(tmp) / (2 * len(x))
return SSE
def draw_hill(x,y):
a = np.linspace(-20,20,100)
print(a)
b = np.linspace(-20,20,100)
x = np.array(x)
y = np.array(y)
allSSE = np.zeros(shape=(len(a),len(b)))
for ai in range(0,len(a)):
for bi in range(0,len(b)):
a0 = a[ai]
b0 = b[bi]
SSE = calc_loss(a=a0,b=b0,x=x,y=y)
allSSE[ai][bi] = SSE
a,b = np.meshgrid(a, b)
return [a,b,allSSE]
def shuffle_data(x,y):
seed = random.random()
random.seed(seed)
random.shuffle(x)
random.seed(seed)
random.shuffle(y)
def get_batch_data(x,y,batch=3):
shuffle_data(x,y)
x_new = x[0:batch]
y_new = y[0:batch]
return [x_new,y_new]
x = [30 ,35,37, 59, 70, 76, 88, 100]
y = [1100, 1423, 1377, 1800, 2304, 2588, 3495, 4839]
x_max = max(x)
x_min = min(x)
y_max = max(y)
y_min = min(y)
for i in range(0,len(x)):
x[i] = (x[i] - x_min)/(x_max - x_min)
y[i] = (y[i] - y_min)/(y_max - y_min)
[ha,hb,hallSSE] = draw_hill(x,y)
hallSSE = hallSSE.T
a = 10.0
b = -20.0
fig = plt.figure(1, figsize=(12, 8))
fig.suptitle(‘learning rate: %.2f xlx mini-batch SGD ‘%(rate), fontsize=15)
ax = fig.add_subplot(2, 2, 1, projection=’3d’)
ax.set_top_view()
ax.plot_surface(ha, hb, hallSSE, rstride=2, cstride=2, cmap=’rainbow’)
plt.subplot(2,2,2)
ta = np.linspace(-20, 20, 100)
tb = np.linspace(-20, 20, 100)
plt.contourf(ha,hb,hallSSE,15,alpha=0.5,cmap=plt.cm.hot)
C = plt.contour(ha,hb,hallSSE,15,colors=’black’)
plt.clabel(C,inline=True)
plt.xlabel(‘a’)
plt.ylabel(‘b’)
plt.ion() # iteration on
all_loss = []
all_step = []
last_a = a
last_b = b
for step in range(1,200):
loss = 0
all_da = 0
all_db = 0
shuffle_data(x,y)
[x_new,y_new] = get_batch_data(x,y,batch=4)
for i in range(0,len(x_new)):
y_p = a*x_new[i] + b
loss = loss + (y_new[i] - y_p)*(y_new[i] - y_p)/2
all_da = all_da + da(y_new[i],y_p,x_new[i])
all_db = all_db + db(y_new[i],y_p)
#loss_ = calc_loss(a = a,b=b,x=np.array(x),y=np.array(y))
loss = loss/len(x_new)
ax.scatter(a, b, loss, color=’black’)
plt.subplot(2,2,2)
plt.scatter(a,b,s=5,color=’blue’)
plt.plot([last_a,a],[last_b,b],color=’aqua’)
plt.subplot(2, 2, 3)
plt.plot(x, y)
plt.plot(x, y, ‘o’)
x_ = np.linspace(0, 1, 2)
y_draw = a * x_ + b
plt.plot(x_, y_draw)
all_loss.append(loss)
all_step.append(step)
plt.subplot(2,2,4)
plt.plot(all_step,all_loss,color=’orange’)
plt.xlabel(“step”)
plt.ylabel(“loss”)
# print(‘a = %.3f,b = %.3f’ % (a,b))
last_a = a
last_b = b
a = a - rate*all_da
b = b - rate*all_db
if step%1 == 0:
print(“step: “, step, ” loss: “, loss)
plt.show()
plt.pause(0.01)
plt.show()