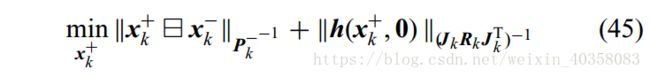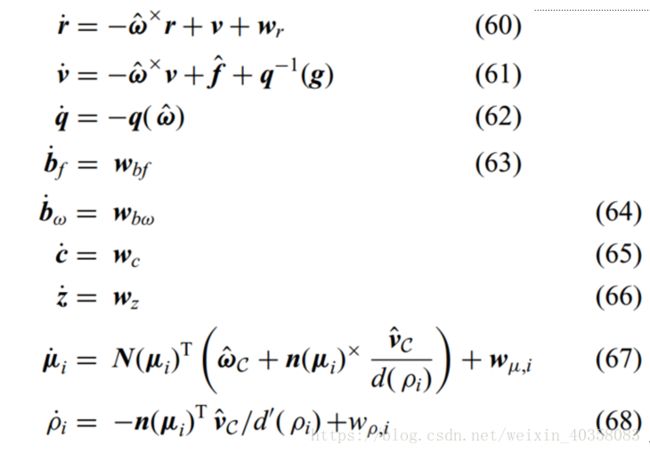ROVIO论文笔记
最近看了ROVIO的相关论文【1-3】。[1]是15年作者发表的会议论文，内容特别简要，根本看不懂。[3]是作者发表在杂志上的论文，对【1】进行了改进，内容也进行了大量的扩充。【2】是作者16年发表的关于上边两篇论文中需要用到的关于姿态在李群和李代数上的求导问题的详细推导。本篇博客主要是针对【3】Iterated extended Kalman filter based visual -inertial odometry using direct photometric feedback这一篇论文进行介绍。说实话，有些地方作者并没有讲太清楚，网上相关的博客也不多，全是靠自己的理解。在这里跟大家分享一下本人对于ROVIO论文阅读的理解。有理解不对的地方还请大家见谅。
一、VIO简介
https://blog.csdn.net/xiaoxiaowenqiang/article/details/81192045
上边这篇博客对VIO进行较详细的介绍和分类，里边也包括本文的ROVIO。但是上边那篇博客提供的都是ROVIO的开源代码的一些复现，对ROVIO论文算法并没有怎么涉及。
简单来说，VIO主要是视觉和IMU的一种数据融合。IMU弥补了视觉在一些因为光照变化强烈、弱纹理等原因无法对特征点进行跟踪的问题。而视觉又弥补了IMU随着时间延长而导致的漂移越来越大的问题。
本篇VIO属于紧耦合的VIO。因为作者将视觉信息加入到了状态变量中，与IMU所测量得到的信息进行了滤波融合。
二、IMU简介
从零开始的 IMU 状态模型推导
上边这篇博客对IMU的状态模型、观测模型还有误差模型进行了详细的推导，很值得学习。其中还涉及到了刚体在三维空间中的运动方程（因为ROVIO涉及到了三个坐标系之间的相互转换，所以说读者需要对刚体的运动方程有一定的理解）。
三、话不多说，开始正文
1、摘要
ROVIO这篇文章阐述了一个将视觉信息和IMU信息进行紧耦合的一种视觉惯性测量单元。数据融合的方法主要是通过迭代卡尔曼滤波来进行的。对于视觉方面的信息，作者主要是通过将路标点在图像中对应的点周围的图像块做为路标点的描述子，从而得到光度误差。然后将光度误差进行变换得到IEKF中的innovation term，进而进行滤波状态的更新。整体的滤波方程的构造是以机器人为中心进行构造的（fully robocentric）——实际上这个robocentric就是以IMU为原点固连在IMU上的坐标系——这样可以减小因非线性而造成的误差。此外，作者还将路标点的空间位置信息拆开成了两项。一项是bearing vector（二维向量），还有一项是distance（这里实际上用的是逆深度）。这样的构造方式可以使得初始化没有延迟（下边会有解释）。总体来说，这个ROVIO的鲁棒性和精度还是不错的。作者后边和okvis进行了比较。
2、符号表示
对于C(q),本人认为这个定义是冗余的。因为SO(3)的定义本身就是旋转矩阵，已经是一个3*3的矩阵了。所以觉得没有必要用这个映射。不过既然作者用了，咱们就按照这个记法来。这里的
实际上是
, 即IMU坐标系相对于惯性系的速度。
3、3D旋转的表示
这里需要涉及到李群和李代数的知识。所以本人在这里做一下简单的介绍。详细的李群和李代数的知识可以参考《State Eastimation for Robotics》
3.1 李群SO(3)
3.2 李代数so(3)
3.3 李群和李代数之间的转换
李群R和李代数
(符号^在论文中表示为
。与向量作用表示叉乘）间可以通过exp和log进行转换：
上边这两个公式实际上对应的是论文中的如下两个公式：
有了李群和李代数的知识，就可以定义在李群上的加减法了：
其中
为李群上的乘法（实际上就是矩阵的乘法）。
定义了加减法后，就可以进一步类比实数域上的导数定义来定义关于李群的导数了：
这里的x是三维向量。q(x)表示由向量x确定的旋转矩阵q(x)=exp(x^)。作用于x的加减号为平常我们用的加减号，而作用于q的加减号为定义的.
、
。
对旋转矩阵有了导数的定义后，就可以进行一系列的求导工作：
以上式子的推导公式请参见[2]A Primer on the Differential Calculus of 3D Orientations
4、3D单位向量的表示
这里边作者主要是通过定义的
来实现三维向量额二维向量的转换，从而实现将一个三维的方向向量表达为二维下的bearing vector。具体的原理本人并没有太看懂，这里就不详细介绍这一块了。论文中作者是通过参考Hertzberg C, Wagner R, Frese U, et al. (2011) Integrating generic sensor fusion algorithms with sound state representations through encapsulation of manifolds. Information Fusion
14(1): 57–77.提出了这一个映射。下边是映射的定义以及相关的加减法。
下图是作者给出的一个示意图：
5、光度误差：
作者通过对图像进行2-3层的降采样，然后以提取的特征点p为圆心，对每一层图像提取6*6的图像块（patch）。光度误差的计算都是基于图像块的。具体的公式如下：
作者在这里对这个公式的表述不太清楚。以下是我对这个光度误差的理解：
表示的是预测值(predicted)。其中
表示的是预测的6*6的投影块patch内各个像素点相对于patch中心的坐标（如果是patch的中心点，那么为0）。
表示的是测量值(measured)。那么这里边的
要怎么理解呢？
这里边就牵扯到两张图像了。
如上图所示，在左边这幅图像（参考帧）中，空间中的点P对应于图像中的特征点p（红色的点），基于这个特征点p，可以提取一个6*6的patch（红色的方框）。通过论文中的warping matrix D，可以将参考帧中的patch转换到右边的这幅图像（当前帧）中。在当前帧中相同的像素坐标点p周围的patch不再是6*6的方形块，因为warping matrix 的作用它发生了形变（当前帧中的红色框）。这个红色框（patch）就为式（35）中的测量值。而通过IEKF会有一个基于参考帧中的bearing vector 
的一个预测值
(即点P在当前帧中的bearing vector），在图中用黄点表示。以黄点为中心有一个6*6的patch，作为预测值。这样就有了两个patch，就可以进行相减了。（35）中的参数a和b主要是考虑到了光照变化等影响，对第二张图像进行了修正。
有了式（35）的光度误差，我们就可以把各个图像层的每个特征点的光度误差表达出来，将它们放到一个向量中，组成了下式中的
:
上式对光度误差b进行了一阶泰勒展开，其中A为雅克比矩阵。这个式子在后边IEKF的流程中会经过一个小的变化从而形成innovation term。
到这里，我们就把光度误差模型讲清楚了。
6、IEKF框架
熟悉卡尔曼滤波的的都知道，滤波算法关键的式子是状态方程（39）和观测方程（40）。这里的观测方程和平常的观测方程不太一样。这里的h对应的是像素快patch的光度误差，经过适当的变形后，直接作为滤波算法的innovation term（在常规的卡尔曼滤波算法的innovation term的形式是y-h,而这里的innovation term为h）。
（41）（42）为常规的预测步骤。其中F和G分别为f相对于状态x和噪声w的偏导。
接下来的更新步骤就类似于EKF，都是通过最小化目标函数（45）来完成。
具体的更新过程对应论文中的公式（50-53）
以上四步进行n次迭代，直到收敛。然后进行P的更新
7.运动方程
7.1状态向量的定义
状态向量主要有以下9种元素构成：
这里边的状态变量除了路标点
这两个变量是在相机坐标系下，剩下的都是在IMU的坐标系下，也就是作者说的fully robocentric formation。
这里的部分变量个人觉得作者的表述不太清楚，我理解花了些时间（可能是比较笨吧-_-||）。为了读者更好的理解，在这里做一些解释。
以上的截图内容是论文中的解释。
其中
是IMU相对于惯性系的距离在IMU坐标系下的表示。它实际上满足：
。这里的q表示旋转（会在下边介绍），
就是我们平常意义下的绝对距离。
同理，
表示的是IMU相对于惯性系的速度在IMU坐标系下的表示。写得更具体一点应该是
.。它满足：
。这里的
就是我们平常意义下的绝对速度。
表示惯性系和IMU坐标系之间的旋转矩阵。它可以将B坐标系下的向量映射到 I 坐标系下。它的逆可以将 I 坐标系下的向量映射到B坐标系下。
剩下的一些变量就比较好理解啦，这里就不赘述啦。
7.2运动方程及状态传播
我们能从IMU获得的数据实际上是加速度和角速度，即论文中的
以及
。注意，这里的
。这两个观测量的意义同7.1中相似。
IMU测量的的数据实际上是包含零偏和噪声的数据。而我们估计的加速度和角速度是只包含噪声，而对零偏进行修正了的。论文中，作者给出的估计值为：
个人觉得有点问题，因为这个估计值也把测量噪声去掉了。笔者认为不应该减去
（如果笔者理解有误还望告知）。
接下来，可以通过估计的角速度
和来得到相机的速度和角速度：
其中，
, 
。下边将这个两个公式给大家推导一下，这样方便理解。这里为了表述方便，就不给变量加^了。
这里边第一项表示相机相对于惯性系的绝对线速度，第二项表示因为旋转而产生的附加速度。
因为IMU坐标系B和相机坐标系C是固连的，所以它们可以看成一个整体。所以B的线速度就是C的线速度,B的角速度就是C的角速度（而两者之所以表现出来的总体速度不一样，是因为相对于惯性系原点I的距离不一样，从而其旋转产生的附加速度不一样）。
所以有：
其中
， 
, 将这两个式子代入上式：
则有
![v_C=_Cv_{IC}=(q_{CB})_Bv_{IC}=(q_{CB})(q_{BI})_Iv_{IC}\\=(q_{CB})(q_{BI})[_I\overline{v}_{IB}+((q_{IB})_B\omega_{IB})\times_Ir_{IB}+(q_{IB})\(_B\omega_{IB}\times(_Br_{BC}))]](http://img.e-com-net.com/image/info8/29bfd921c2b6492faa1633296f57c861.gif){kind=small}
![=(q_{CB})[_B\overline{v}_{IB}+_B\omega_{IB}\times_Br_{IB}+_B\omega_{IB}\times_Br_{BC}]](http://img.e-com-net.com/image/info8/dbdc8a87a4474fe99a0fe18a91cf27e8.gif){kind=small}
其中
,
,这样我们就得到了式（58）
对于式（59），我们只需要用到B的角速度和C的角速度相同这一条件即可。
论文（60）-（68）给出了状态微分方程：
这里需要说明的是，（60）给出的是线速度，所以要用和速度v减去因为旋转而产生的速度。加速度同理（注意这里估计的加速度是不包含g的，所以要在计算的时候要把重力加速度考虑进去）。（67,68）的具体推导在附录中有。
然后将以上的微分方程进行一阶泰勒展开，得到更新方程。
7.3 innovation term
(36)式是基于patch 的光度误差。其中A是雅克比矩阵。为了降为，作者这里边用了QR分解：
我们将上式代入（36式），同时做一个变换：
可以看到，更新量
只和
有关。所以，论文中将降维后的b作为innovation term，如（74）所示。
对应的雅克比矩阵也转化成了（75）
8、landmark management
因为landmark是要不停地往状态向量中增广的，所以需要对landmark有效的管理，避免冗余。作者主要是通过两方面进行landmark筛选。一方面，通过Hessian矩阵的最小特征值对landmark的质量进行评判，然后通过quality-score进行二次筛选。不过论文中并没有写具体怎么实现，应该可以在源码中看。这里也就不过多解释了。
9、 流程图
最后给大家分析一下流程图，以便对整个系统的工作流程有个了解。
图中标注了每一步对应的公式。
对于一开始，我们先在第一张图片中提取特征点，并对landmark对应的参数（方向和距离）进行估计。通过quality score computation and pruning，筛选出第一张图像中的特征点。对特征点进行patch提取，同时通过warping matrix将patch投影到第二张图片上，作为measurement。另一方面，我们因为一开始估计了第一张图中特征点对应的landmark参数的估计值，我们可以通过Kalman prediction进行状态预测，即预测landmark在第二张图中的位置。通过预测的patch和measurement计算光度误差，然后通过光度误差计算innovation term，进而进行Kalman update。然后进行循环更新，直到状态向量收敛。收敛后进行outlier的剔除，得到跟踪的第一张图片上的路标点在第二张图片上的最终位置，得到
,然后进入下一轮的运算。
四、结束语
以上就是本人看ROVIO的相关理解。个人感觉还是有些难度的，如果有理解不到位的地方或者有什么理解错误的地方还望指出。
本文为作者原创。转载请注明：https://blog.csdn.net/weixin_40358083/article/details/83088591