分治法解决最近点对问题（C++）

分治法解决最近点对问题（C++）

注意：
这主要是作为我个人的笔记，因此是按照我个人的思路、以最通俗易懂的形式讲解，会有一些不严谨的地方。请选择性参考，若有很大的错误，也希望大家及时指正，谢谢！

步骤：
1.划分
（1）求中位线，将点集以中位线为界，分为左右两部分。
（2）继续找左右两部分的中位线，继续划分。
（3）直到中位线左右两部分的点的个数小于等于二为止。

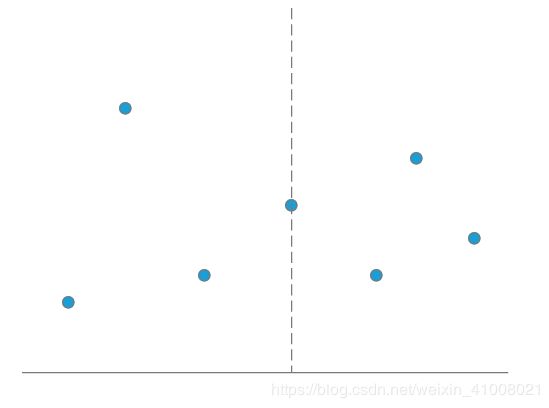
左半部分继续划分，右半部分同理

2.求最小端点间距
（1）求中位线左边部分最小端点间距1；
求中位线右边部分最小端点间距2；
（2）比较1和2，取小的为min；
（3）如果中位线两边距离中位线最近的两点，到中位线的距离均小于min，说明这两点的间距有可能小于min。计算该两点的间距3，如果小于min，则更新min。

简而言之
1）求左边最小
2）求右边最小
3）如果需要，求中位线两边距离中位线最近两点距离
4）取三者最小

函数功能介绍：

//生成端点
void createPoint(Point p[],int num);//two-dimension
void createPoint(int p[],int num);//one-dimension
//计算点间间距
near_Points calDistance(Point p1,Point p2);//two-dimension
near_Points_one calDistance(int x1,int x2);//one-dimension
//计算横坐标中位数
float middlePointx(Point p[],int num);//two-dimension
float middlePointx(int p[],int num);//one-dimension
//分治法递归求最近点
near_Points Conquer(Point p[],int num);//two-dimension
near_Points_one Conquer(int p[],int num);//one-dimension

啊啊啊啊~因为一维的是后来加上去的,懒得整合在一起了，函数有些多，有些啰嗦 ~

完整代码：

#include 
#include 
#include 
using namespace std;
//端点类
class Point{//二维
public:
    int x;
    int y;
};
//最近点对类
class near_Points{
public:
    Point pl;
    Point pr;
    float distance;
};
class near_Points_one{
public:
    int x1;
    int x2;
    int distance;
};
//随机生成端点
void createPoint(Point p[],int num)//two-dimension
{
    int i;
    for(i=0;i<num;i++)
    {
        p[i].x=rand()%50;
        p[i].y=rand()%50;
    }
}
void createPoint(int p[],int num)//one-dimension
{
    int i;
    for(i=0;i<num;i++)
    {
        p[i]=rand()%50;
    }
}
//计算两点之间的距离
near_Points calDistance(Point p1,Point p2)//two-dimension
{
    near_Points tps;
    tps.pl=p1;
    tps.pr=p2;
    tps.distance=sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
    return tps;
}
near_Points_one calDistance(int x1,int x2)//one-dimension
{
    near_Points_one np;
    if(x1>x2)
    {
        np.x1=x1;
        np.x2=x2;
        np.distance=x1-x2;
    }
    else
    {
        np.x1=x2;
        np.x2=x1;
        np.distance=x2-x1;
    }
    return np;
}
//排序,取横坐标的中位数
float middlePointx(Point p[],int num)//two-dimension
{
    int i,j;
    float mid;
    Point temp;
    for(i=0;i<num-1;i++)
        for(j=0;j<num-1-i;j++)
            if(p[j].x>p[j+1].x)
            {
                temp=p[j];
                p[j]=p[j+1];
                p[j+1]=temp;
            }
    if(num%2==0)
        mid=(p[num/2-1].x+p[num/2].x)/2;
    else mid=p[num/2].x;
    return mid;
}
float middlePointx(int p[],int num)//one-dimension
{
    int i,j;
    float mid;
    int temp;
    for(i=0;i<num-1;i++)
        for(j=0;j<num-1-i;j++)
            if(p[j]>p[j+1])
            {
                temp=p[j];
                p[j]=p[j+1];
                p[j+1]=temp;
            }
    if(num%2==0)
        mid=(p[num/2-1]+p[num/2])/2;
    else mid=p[num/2];
    return mid;
}
//分治法,将端点分为中位线两侧两个集合
near_Points Conquer(Point p[],int num)//two-dimension
{
    float mid;
    near_Points tps,tps1,tps2,tps3;
    //端点数小于2,不作任何操作,直接返回
    if(num<2) return tps;
    //端点数等于2,计算两个端点之间的距离
    else if(num==2)
    {
        tps=calDistance(p[0],p[1]);
        return tps;
    }
    //端点数大于2,继续分组
    else
    {
        mid=middlePointx(p,num);
        //分为端点数为奇数或偶数两种情况
        if(num%2==0)//偶数情况
        {
            tps1=Conquer(p,num/2);
            tps2=Conquer(p+num/2,num/2);
            if(tps1.distance<tps2.distance)
                tps=tps1;
            else tps=tps2;
            //检查距离中位线最近的两个端点距离是否为最小距离
            if(mid-p[num/2-1].x<tps.distance)
            {
                if(p[num/2].x-mid<tps.distance)
                {
                    tps3=calDistance(p[num/2-1],p[num/2]);
                    if(tps3.distance<tps.distance)
                        tps=tps3;
                }
            }
        }
        else//奇数情况
        {
            tps1=Conquer(p,num/2+1);
            tps2=Conquer(p+num/2+1,num/2);
            if(tps1.distance<tps2.distance)
                tps=tps1;
            else tps=tps2;
            //检查距离中位线最近的两个端点距离是否为最小距离
            if(mid-p[num/2].x<tps.distance)
            {
                if(p[num/2+1].x-mid<tps.distance)
                {
                    tps3=calDistance(p[num/2],p[num/2+1]);
                    if(tps3.distance<tps.distance)
                        tps=tps3;
                }
            }
        }
        return tps;
    }
}
near_Points_one Conquer(int p[],int num)//one-dimension
{
    float mid;
    near_Points_one tps,tps1,tps2,tps3;
    //端点数小于2,不作任何操作,直接返回
    if(num<2) return tps;
    //端点数等于2,计算两个端点之间的距离
    else if(num==2)
    {
        tps=calDistance(p[0],p[1]);
        return tps;
    }
    //端点数大于2,继续分组
    else
    {
        mid=middlePointx(p,num);
        //分为端点数为奇数或偶数两种情况
        if(num%2==0)//偶数情况
        {
            tps1=Conquer(p,num/2);
            tps2=Conquer(p+num/2,num/2);
            if(tps1.distance<tps2.distance)
                tps=tps1;
            else tps=tps2;
            //检查距离中位线最近的两个端点距离是否为最小距离
            if(mid-p[num/2-1]<tps.distance)
            {
                if(p[num/2]-mid<tps.distance)
                {
                    tps3=calDistance(p[num/2-1],p[num/2]);
                    if(tps3.distance<tps.distance)
                        tps=tps3;
                }
            }
        }
        else//奇数情况
        {
            tps1=Conquer(p,num/2+1);
            tps2=Conquer(p+num/2+1,num/2);
            if(tps1.distance<tps2.distance)
                tps=tps1;
            else tps=tps2;
            //检查距离中位线最近的两个端点距离是否为最小距离
            if(mid-p[num/2]<tps.distance)
            {
                if(p[num/2+1]-mid<tps.distance)
                {
                    tps3=calDistance(p[num/2],p[num/2+1]);
                    if(tps3.distance<tps.distance)
                        tps=tps3;
                }
            }
        }
        return tps;
    }
}
int main()
{
    int choice;
    int num,i;
    cout<<"One-dimension choose 1,two-dimension choose 2:";
    cin>>choice;
    //生成端点
    cout << "Input the number of points:";
    cin>>num;
    cout<<"The number of points is "<<num<<endl;
    cout<<"Create points..."<<endl;
    if(choice==1)
    {
        int op[100];
        near_Points_one pso;
        createPoint(op,num);
        cout<<"Create completed!"<<endl;
        cout<<"Points:"<<endl;
        for(i=0;i<num;i++)
        {
            cout<<"Output the No."<<i+1<<" point:";
            cout<<"x="<<op[i]<<endl;
        }
        //从此处开始寻找最近点对
        pso=Conquer(op,num);
        //输出最近点对信息
        cout<<"The nearest points are :"<<endl;
        cout<<"Point_1:x="<<pso.x1<<endl;
        cout<<"Point_2:x="<<pso.x2<<endl;
        cout<<"Distance:"<<pso.distance<<endl;
    }
    else if(choice==2)
    {
        Point p[100];
        near_Points ps;
        createPoint(p,num);
        cout<<"Create completed!"<<endl;
        cout<<"Points:"<<endl;
        for(i=0;i<num;i++)
        {
            cout<<"Output the No."<<i+1<<" point:";
            cout<<p[i].x<<"  "<<p[i].y<<endl;
        }
        //从此处开始寻找最近点对
        ps=Conquer(p,num);
        //输出最近点对信息
        cout<<"The nearest points are :"<<endl;
        cout<<"Point_1:("<<ps.pl.x<<","<<ps.pl.y<<")"<<endl;
        cout<<"Point_2:("<<ps.pr.x<<","<<ps.pr.y<<")"<<endl;
        cout<<"Distance:"<<ps.distance<<endl;
    }
    cout<<"Finished!"<<endl;
}

运行结果：
一维结果

二维结果

道谢~