基于分位数回归的分布强化学习(Distributional Reinforcemet Learning with Quantile Regression)
摘要
Deep Mind团队联合剑桥大学在2017年提出了一种新的强化学习范式——基于分位数回归的分布强化学习(QR-DRL),为强化学习的未来发展指明了一个更加有前景的方向,以学习回报值的概率分布来代替学习回报值的期望值。Deep Mind的论文通过在atari游戏中的实验,证明了QR-DRL的强大性能,在众多游戏中都达到了state-of-art。私以为QR-DRL是近年来为数不多的,从根本理论上对强化学习的创新发展,分布强化学习将会在未来的几年里成为强化学习领域的研究热点之一。
QR-DRL的理论基础
牛顿说过:“如果说我看得比别人更远些,那是因为我站在巨人的肩膀上。”QR-DRL也是在众多前人的研究基础上提出的。想要理解QR-DRL,就不得不提到以下几个概念:
1. Distributional RL(分布强化学习)
2. The Wasserstein Metric(瓦瑟斯坦度量)
3. Quantile Regression(分位数回归)
1.分布强化学习
我们先来讲将分布强化学习吧。简单来说,传统RL如Q-learning学习的是回报值的未来期望值:
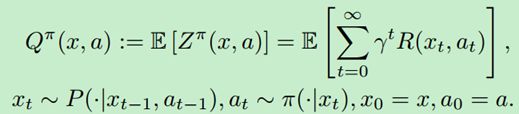
其中,
![]()
表示在遵循策略π的情况下,表示未来总折扣收益的随机变量。而在分布强化学习中,我们要学习的是这个随机变量所满足的概率分布。2017年,Bellemare等人在他们工作中将这种学习概率分布的思想拓展到强化学习中,并提出了分布贝尔曼算子(distributional Bellman operator):
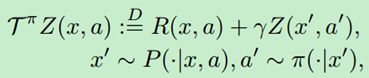
在他们的论文中,Bellemare等人还提出了最早的分布强化学习算法——C51。简单来说,C51分为两步:1.启发式投影。2.最小化投影后的Bellman更新分布与预测分布之间的KL散度。
先来解释一下第一步的投影到底是个什么玩意儿。要想学习一个概率分布,你首先要找到一种方式来表示这个概率分布。C51的做法是,以若干个固定位置 z 1 < . . . < z N z_{1}<...<z_{N} z1<...<zN作为支撑,建立一个离散分布 Z π ( x , a ) Z^{\pi }\left ( x,a \right ) Zπ(x,a)。这些固定位置在一个预先确定的间隔中均匀分布。在每个位置 z i z_{i} zi的概率 q i q_{i} qi构成了分布的参数, q i q_{i} qi由logits模型来表示。在给定一个当前值分布下,C51通过一个投影操作 Φ \Phi Φ将目标 T π Z T^{\pi }Z TπZ投影到其有限个支撑位置上。最后通过一个KL最小化步骤进行更新。
C51可以形象化成下图:
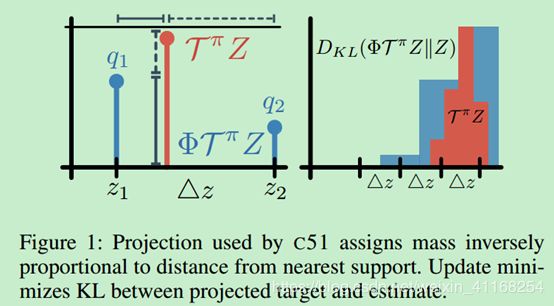
Bellemare等人工作的贡献除了C51算法,还证明了分布贝尔曼算子是概率分布之间Wasserstein度量极大形式的收缩。Wasserstein度量能够有效避免执行贝尔曼更新时产生的disjoint-support问题。与Kullback-Leibler散度不同,Wasserstein度量是一个真实的概率度量,它同时考虑各种结果事件的概率和它们之间的距离。即使Wasserstein度量是如此地契合分布强化学习,不幸的是 Bellemare等人指出,Wasserstein度量作为一种损失,是无法由随机梯度下降来进行最小化的。C51算法中使用了KL散度来替代Wasserstein度量,虽然在atari游戏中取得了state-of-art,但是其收敛性与有效性均没有理论支撑。
2.The Wasserstein Metric(瓦瑟斯坦度量)
分布U与Y间的p-Wasserstein度量 W p W_{p} Wp的表达式如下:
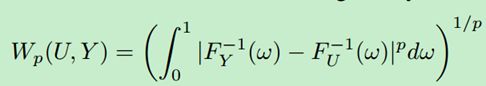
其中
![]()
F Y ( y ) = P r ( Y ≤ y ) F_{Y}\left ( y\right )=Pr\left ( Y\leq y \right ) FY(y)=Pr(Y≤y)为Y的累积分布函数(CDF)。两个CDF间的区域即为1-Wasserstein距离:
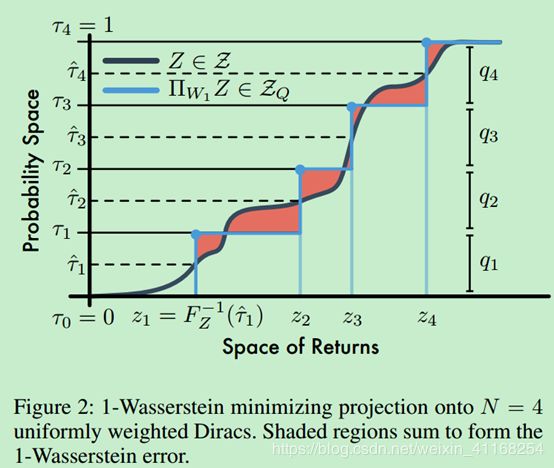
Bellemare等人基于Wasserstein距离对分布贝尔曼算子的收敛性做了证明。
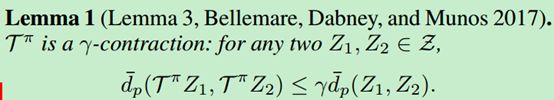
其中,
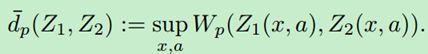
表示两个动作值分布间的p-Wasserstein度量的上确界。
我们前文提到了,Bellemare等人证明了Wasserstein度量无法由随机梯度下降进行最小化。那么,如何才能克服这个问题呢?Deep Mind给出了他们的答案。
回想一下C51近似分布的做法是给固定位置 z i z_{i} zi分配不同的概率 q i q_{i} qi。而Deep Mind将此方法进行了“转置”:位置不同而概率固定,即 q i = 1 / N q_{i}=1/N qi=1/N,i=1,…,N。这种新的近似方法目的在于估计目标分布的quantiles(分位数),因此称之为分位数分布,用 Z Q Z_{Q} ZQ表示固定N的分位数分布。此分布的累计概率表示为 τ 1 , . . . , τ N \tau _{1},...,\tau _{N} τ1,...,τN, τ i = i N , i = 1 , . . . , N \tau _{i}=\frac{i}{N},i=1,...,N τi=Ni,i=1,...,N。用 θ : χ × A → R N \theta :\chi \times A\rightarrow R^{N} θ:χ×A→RN表示参数化模型,一个分位数模型 Z θ ∈ Z Q Z_{\theta }\in Z_{Q} Zθ∈ZQ将每一个状态动作对(s,a)映射到一个均匀概率分布上,此概率分布由 { θ i ( x , a ) } \left \{ \theta_{i} \left ( x,a \right ) \right \} {θi(x,a)}支撑:
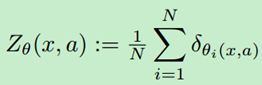
其中 δ z \delta _{z} δz表示在z处的狄拉克函数。
Deep Mind总结了这种表示方法的改进所带来的的好处:
- 不再受限于预先确定的支撑的界限,当回报值的范围很大时,能够进行更精确的预测
- 避免了C51中的投影操作
- 这种再参数化允许我们使用分位数回归来最小化Wasserstein损失,而不受有偏梯度的影响。
3.Quantile Regression(分位数回归)
接下来就是重头戏——分位数回归,它是分布强化学习算法的核心所在。首先介绍一下分位数投影的概念。我们使用
![]()
来对值分布Z投影到 Z Q Z_{Q} ZQ进行量化。设Y为第一矩有界的分布,U为N个狄拉克函数组成的均匀分布,支撑为 { θ 1 , . . . , θ N } \left \{ \theta _{1},...,\theta _{N} \right \} {θ1,...,θN}。则
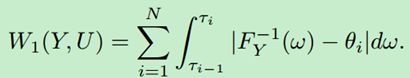
根据lemma 2:
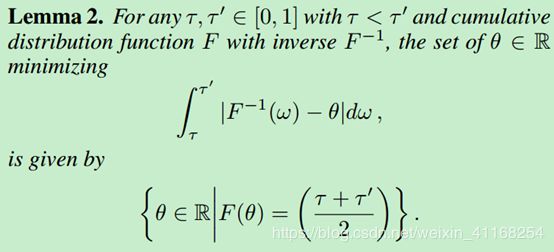
可知,最小化 W 1 ( Y , U ) W_{1}\left ( Y,U \right ) W1(Y,U)的支撑 { θ 1 , . . . , θ N } \left \{ \theta _{1},...,\theta _{N} \right \} {θ1,...,θN}的值为 θ i = F Y − 1 ( τ ^ i ) \theta _{i}=F_{Y}^{-1}\left ( \hat{\tau }_{i} \right ) θi=FY−1(τ^i), τ ^ i = ( τ i − 1 + τ i ) / 2 \hat{\tau }_{i}=\left ( \tau _{i-1}+\tau _{i} \right )/2 τ^i=(τi−1+τi)/2, 1 ≤ i ≤ N 1\leq i\leq N 1≤i≤N。
为了解决有偏梯度问题,使用了分位数回归来进行分位数函数的无偏随机逼近。对于一个分布Z以及一个给定的分位数 τ \tau τ,分位数函数 F Z − 1 ( τ ) F_{Z}^{-1}\left ( \tau \right ) FZ−1(τ)的值能够由分位数回归损失的最小化来体现:
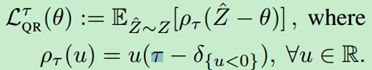
更一般地,结合lemma 2我们得到如下目标:
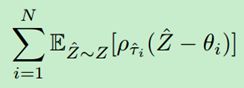
特别是,这种损失给出了无偏样本梯度。因此,我们可以通过随机梯度下降来找到最小化 { θ 1 , . . . , θ N } \left \{ \theta _{1},...,\theta _{N} \right \} {θ1,...,θN}。
进一步,Deep Mind提出了一个平滑版本的损失Quantile Huber Loss :
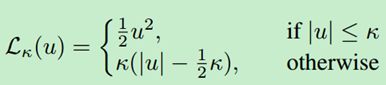
![]()
至此,我们已经完成了QR-DRL核心理论的介绍,关于分位数投影下的贝尔曼更新的收敛性证明不过多阐述。接下来就是形成一个完整算法。
QR-DQN
算法的大体思路是:利用一个参数化的分位数分布来近似动作值分布,分位数分布由一系列lemma 2定义的分位数中点形成。然后使用分位数回归来训练位置参数。
由此提出quantileregression temporal difference learning (QRTD) 算法:
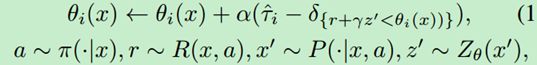
将QRTD应用到DQN上,形成QR-DQN算法,分布贝尔曼算子:
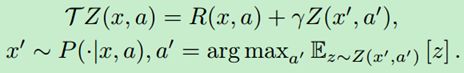
QR-DQN对DQN进行三处修改:1.输出层尺寸改为 ∣ A ∣ × N \left | A \right |\times N ∣A∣×N,N为分位数目标的数目。2.目标函数改为Quantile Huber Loss。3.使用Adam代替RMSProp。具体算法如下:

随着N的增加,值分布的估计精度也增加。
结语
QR-DRL的提出大大拓展了强化学习的理论基础。从期望学习到分布学习,使得强化学习的性能有了质的提升。基于QR-DRL势必有更多的分布强化学习的新应用与变体被提出来,接下来,我将持续关注分布强化学习的研究进展,尽量将分布强化学习族算法做一个全面的介绍。
Deep Mind原文链接: QR-DRL原文