不均衡学习
一、简介
在很多场景的数据集中,都会出现某一类数据的数量远远多于其它类的数据,一般都是以二分类的类别不平衡问题为主。一个简单的理解,假如某个数据集,10万个正样本(正常用户标签为0)与1000个负样本(有问题用户标签为1),正负样本比例为100:1,如果模型学习每一次梯度下降使用全量样本,负样本的权重不到1/100,即使完全不学习负样本的信息,准确率也有99%,所以实际应用中不能完全用准确率衡量模型的效果,还会使用AUC等指标衡量模型的表现,但是依然没有办法保证模型将负样本很好的学习,这个例子就是说明数据集中正例和负例不平衡。为了使模型即对正例有很高的的准确率也对负例有很好的准确率,需要保持数据集相对平衡。
二、解决数据不平衡方法
通常解决数据不平衡的方法有下探、半监督学习、标签分裂、代价敏感、采样算法,下面为具体介绍:
(一) 下探
下探是最直接解决风控场景样本不均衡的方法。所谓下探,就是对评分较低被拒绝的人不进行监管,牺牲一部分收益,来积累坏样本,供后续模型学习。此外,随着业务开展,后续模型迭代的时候,使用的样本是有偏的,下探同样可以解决这个问题。
(二) 半监督学习
将有问题用户的数据通过半监督的方法逐渐生成标签,然后带入模型中进行训练。比较典型分方法有拒绝演绎、暴力半监督等等。
1)拒绝演绎
拒绝演绎或者叫拒绝推断,是一种根据经验对低分客户进行百分比采样的方法。比如最低分的客群百分之五十视为坏人,其次百分之四十等等。
2)暴力半监督
比较粗暴的做法是将样本的每一种标签方式进行穷举,带入模型看对模型是否有帮助,效率较低,容易过拟合。
3)模型筛选
用训练过的其他模型对无标签样本打标签,然后模型进行训练。很多公司会用当前模型在上面做预测,然后带入模型继续训练。很不推荐这样做,效果一般是很差的。可以考虑无监督算法或者用很旧的样本做训练然后做预测。
(三) 标签分裂
我们有时候会不止使用传统的一些定义来定义好坏。而是通过一些聚类手段对数据进行切分,然后分别在自己的样本空间内单独学习。基于模型的比如kmeans,分层聚类等等。基于经验的比如将失联客户、欺诈客户拆开,单独建模。
简单的理解如下面这个例子:
张三生了病,她的失散多年的哥哥找到有2家比较好的医院,医院A和医院B供 张三选择就医。
张三的哥哥多方打听,搜集了这两家医院的统计数据,它们是这样的:
医院A最近接收的1000个病人里,有900个活着,100个死了。
医院B最近接收的1000个病人里,有800个活着,200个死了。
作为对统计学懵懵懂懂的普通人来说,看起来最明智的选择应该是医院A对吧,病人存活率很高有90%啊!总不可能选医院B吧,存活率只有80%啊。呵呵,如果 张三的选择是医院A,那么她就中计了。
就这么说吧,如果医院A最近接收的1000个病人里,有100个病人病情很严重,900个病人病情并不严重。
在这100个病情严重的病人里,有30个活下来了,其他70人死了。所以病重的病人在医院A的存活率是30%。
而在病情不严重的900个病人里,870个活着,30个人死了。所以病情不严重的病人在医院A的存活率是96.7%。
在医院B最近接收的1000个病人里,有400个病情很严重,其中210个人存活,因此病重的病人在医院B的存活率是52.5%。
有600个病人病情不严重,590个人存活,所以病情不严重的病人在医院B的存活率是98.3%。
更直观的如下面图片所示:
实际上,我们刚刚看到的例子,就是统计学中著名的黑魔法之一——辛普森悖论(Simpson's paradox)。辛普森悖论就是当你把数据拆开细看的时候,细节和整体趋势完全不同的现象。
(四) 代价敏感
代价敏感学习则是利用不同类别的样本被误分类而产生不同的代价,使用这种方法解决数据不平衡问题。而且有很多研究表明,代价敏感学习和样本不平衡问题有很强的联系,并且使用代价敏感学习的方法解决不平衡学习问题要优于使用随机采样的方法。
1) 把误分类代价作为数据集的权重,然后采用 Bootstrap 采样方法选择具有最好的数据分布的数据集;
2) 以集成学习的模式来实现代价最小化的技术,这种方法可以选择很多标准的学习算法作为集成学习中的弱分类器;
3) 把代价敏感函数或者特征直接合并到分类器的参数中,这样可以更好的拟合代价敏感函数。由于这类技术往往都具有特定的参数,因此这类方法没有统一的框架;
(五) 采样算法
- 朴素随机过采样
from sklearn.datasets import make_classification
from collections import Counter
from imblearn.over_sampling import RandomOverSampler
X, y = make_classification(n_samples=5000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=2,
n_clusters_per_class=1,
weights=[0.01, 0.99],
class_sep=0.8, random_state=0)
Counter(y)
ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_sample(X, y)
sorted(Counter(y_resampled).items())- SMOTE
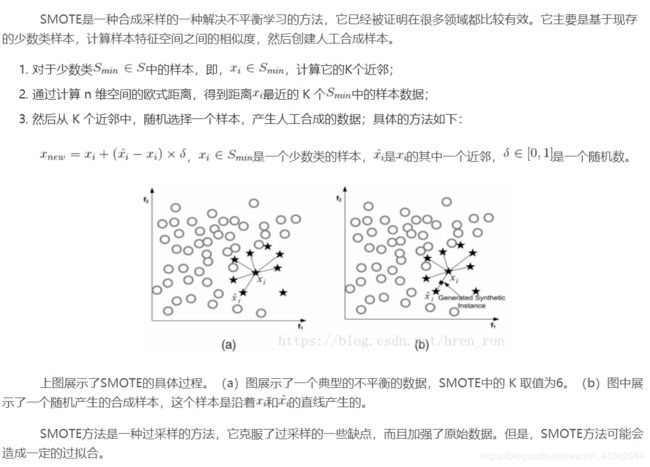
对于少数类样本a, 随机选择一个最近邻的样本b, 然后从a与b的连线上随机选取一个点c作为新的少数类样本;但是,SMOTE容易出现过泛化和高方差的问题,而且,容易制造出重叠的数据。
为了克服SMOTE的缺点,Adaptive Synthetic Sampling方法被提出,主要包括:Borderline-SMOTE和Adaptive Synthetic Sampling(ADA-SYN)算法。
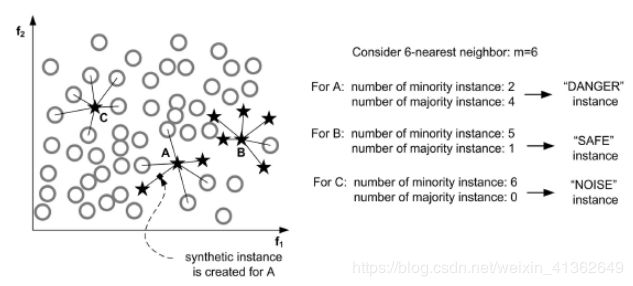
Borderline-SMOTE:对靠近边界的minority样本创造新数据。其与SMOTE的不同是:SMOTE是对每一个minority样本产生综合新样本,而Borderline-SMOTE仅对靠近边界的minority样本创造新数据。如下图,只对A中的部分数据进行操作:
这个图中展示了该方法的实现过程,我们可以发现和SMOTE方法的不同之处:SMOTE对于每一个少数类样本都会产生合成样本,但是Borderline-SMOTE只会对邻近边界的少数类样本生成合成数据。ADA-SYN:根据majority和minority的密度分布,动态改变权重,决定要generate多少minority的新数据。
相对于基本的SMOTE算法, 关注的是所有的少数类样本, 这些情况可能会导致产生次优的决策函数。
因此SMOTE就产生了一些变体,这些方法关注在最优化决策函数边界的一些少数类样本, 然后在最近邻类的相反方向生成样本。、 SMOTE函数中的kind参数控制了选择哪种变体
- regular
- borderline1
- borderline2
- svm
from imblearn.over_sampling import SMOTE, ADASYN
X_resampled, y_resampled = SMOTE(kind='borderline1').fit_sample(X, y)
sorted(Counter(y_resampled).items())三、实际应用
目前应用最多的是smote中变体为borderline1
1)构建baseline - LR模型
import glob
import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV as gscv
from sklearn.neighbors import KNeighborsClassifier
data = pd.read_csv('xxxxx.txt')
train = data[data.obs_mth != '2018-11-30'].reset_index().copy()
evl = data[data.obs_mth == '2018-11-30'].reset_index().copy()
x = train[feature_lst]
y = train['bad_ind']
evl_x = evl[feature_lst]
evl_y = evl['bad_ind']
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(x,y)
y_pred = lr_model.predict_proba(x)[:,1]
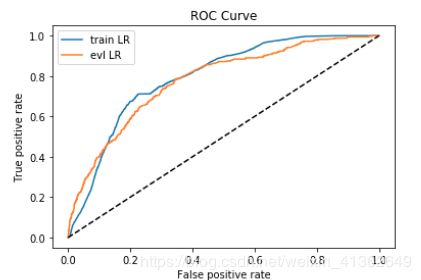
fpr_lr_train,tpr_lr_train,_ = roc_curve(y,y_pred)
train_ks = abs(fpr_lr_train - tpr_lr_train).max()
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(evl_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(evl_y,y_pred)
evl_ks = abs(fpr_lr - tpr_lr).max()
print('evl_ks : ',evl_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR')
plt.plot(fpr_lr,tpr_lr,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()
2) 优化
先用lgb做预测,然后做前融合,相比于不修改损失函数的xgb,lgb的优势只是比较快,思想类似于对训练样本做异常点检测只不过不是根据数据内部分布差异,而是使用精准度更高的集成模型,将难以辨认的样本,视为噪音。
首先做网格调参,给lgb找一组较好的参数
train_x,test_x,train_y,test_y = train_test_split(x,y,random_state=0,test_size=0.4)
params = {
'boosting_type':'gbdt',
'objective':'binary',
'metric':'auc',
'nthread':4,
'learning_rate':0.1,
'num_leaves':30,
'max_depth':5,
'subsample':0.8,
'colsample_bytree':0.8,
}
data_train = lgb.Dataset(train_x,train_y)
cv_results = lgb.cv(params,
data_train,
num_boost_round = 1000,
nfold = 5,
stratified = False,
shuffle = True,
metrics = 'auc',
early_stopping_rounds = 100,
seed = 0
)
print('best n_estimators:',len(cv_results['auc-mean']))
print('best cv score:',pd.Series(cv_results['auc-mean']).max())
best n_estimators: 24
best cv score: 0.8097663177199287
def lgb_test(train_x,train_y,test_x,test_y):
clf =lgb.LGBMClassifier(boosting_type = 'gbdt',
objective = 'binary',
metric = 'auc',
learning_rate = 0.1,
n_estimators = 24,
max_depth = 4,
num_leaves = 25,
max_bin = 40,
min_data_in_leaf = 5,
bagging_fraction = 0.6,
bagging_freq = 0,
feature_fraction = 0.8,
)
clf.fit(train_x,train_y,eval_set = [(train_x,train_y),(test_x,test_y)],eval_metric = 'auc')
return clf,clf.best_score_['valid_1']['auc'],
lgb_model , lgb_auc = lgb_test(train_x,train_y,test_x,test_y)
feature_importance = pd.DataFrame({'name':lgb_model.booster_.feature_name(),
'importance':lgb_model.feature_importances_}).sort_values(by=['importance'],ascending=False)
pred = lgb_model.predict_proba(train_x)[:,1]
fpr_lgb,tpr_lgb,_ = roc_curve(train_y,pred)
print(abs(fpr_lgb - tpr_lgb).max())
pred = lgb_model.predict_proba(test_x)[:,1]
fpr_lgb,tpr_lgb,_ = roc_curve(test_y,pred)
print(abs(fpr_lgb - tpr_lgb).max())
pred = lgb_model.predict_proba(evl_x)[:,1]
fpr_lgb,tpr_lgb,_ = roc_curve(evl_y,pred)
print(abs(fpr_lgb - tpr_lgb).max())
0.5064991567297175
0.48909811193341235
0.41935471928695134
粗略调参的lgb比lr无显著提升,下面进行权重调整。前后各取部分错分样本,减小权重,其余样本为1。虽然后面还会给予新的权重,但是这部分权重永远只有正常样本的固定比例。
sample = x[feature_lst]
sample['bad_ind'] = y
sample['pred'] = lgb_model.predict_proba(x)[:,1]
sample = sample.sort_values(by=['pred'],ascending=False).reset_index()
sample['rank'] = np.array(sample.index)/75522
def weight(x,y):
if x == 0 and y < 0.1:
return 0.1
elif x == 1 and y > 0.7:
return 0.1
else:
return 1
sample['weight'] = sample.apply(lambda x: weight(x.bad_ind,x['rank']),axis = 1)
def lr_wt_predict(train_x,train_y,evl_x,evl_y,weight):
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(train_x,train_y,sample_weight = weight )
y_pred = lr_model.predict_proba(train_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(train_y,y_pred)
train_ks = abs(fpr_lr - tpr_lr).max()
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(evl_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(evl_y,y_pred)
evl_ks = abs(fpr_lr - tpr_lr).max()
print('evl_ks : ',evl_ks)
lr_wt_predict(sample[feature_lst],sample['bad_ind'],evl_x,evl_y,sample['weight'])
train_ks : 0.4602564513254416
evl_ks : 0.4289610959476374此时的lr,相比于最开始的lr,提升了1个百分点。这里省略了一些其他的探索,由于其他算法实验效果不理想,最终选取lgb作为筛选样本的工具。接下来考虑基于差值思想的过采样方法,增加一部分虚拟的负样本。这里需要注意,之前权重减小的样本是不应该用来做过采样的。所以将训练数据先拆分成两部分。weight=1的做过采样,其余的不变。
osvp_sample = sample[sample.weight == 1].drop(['pred','index','weight'],axis = 1)
osnu_sample = sample[sample.weight < 1].drop(['pred','index',],axis = 1)
train_x_osvp = osvp_sample[feature_lst]
train_y_osvp = osvp_sample['bad_ind']
#下面做基于borderline1的smote算法做过采样
def lr_predict(train_x,train_y,evl_x,evl_y):
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(train_x,train_y)
y_pred = lr_model.predict_proba(train_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(train_y,y_pred)
train_ks = abs(fpr_lr - tpr_lr).max()
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(evl_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(evl_y,y_pred)
evl_ks = abs(fpr_lr - tpr_lr).max()
print('evl_ks : ',evl_ks)
return train_ks,evl_ks
from imblearn.over_sampling import SMOTE,RandomOverSampler,ADASYN
smote = SMOTE(k_neighbors=15, kind='borderline1', m_neighbors=4, n_jobs=1,
out_step='deprecated', random_state=0, ratio=None,
svm_estimator='deprecated')
rex,rey = smote.fit_resample(train_x_osvp,train_y_osvp)
print('badpctn:',rey.sum()/len(rey))
df_rex = pd.DataFrame(rex)
df_rex.columns =feature_lst
df_rex['weight'] = 1
df_rex['bad_ind'] = rey
df_aff_ovsp = df_rex.append(osnu_sample)
lr_predict(df_aff_ovsp[feature_lst],df_aff_ovsp['bad_ind'],evl_x,evl_y)
badpctn: 0.5
train_ks : 0.4859866821876423
evl_ks : 0.44085108654818894
下面尝试使用KNN做前融合, 主要思想是knn和逻辑回归对样本的分布先验是相同的, 虽然是弱分类器, 识别出的异常值应该对模型影响更大。
首先寻找最优k值
lr_model = LogisticRegression(C=0.1,class_weight='balanced')
lr_model.fit(df_aff_ovsp[feature_lst],df_aff_ovsp['bad_ind'] )
y_pred = lr_model.predict_proba(df_aff_ovsp[feature_lst])[:,1]
fpr_lr_train,tpr_lr_train,_ = roc_curve(df_aff_ovsp['bad_ind'],y_pred)
train_ks = abs(fpr_lr_train - tpr_lr_train).max()
print('train_ks : ',train_ks)
y_pred = lr_model.predict_proba(evl_x)[:,1]
fpr_lr,tpr_lr,_ = roc_curve(evl_y,y_pred)
evl_ks = abs(fpr_lr - tpr_lr).max()
print('evl_ks : ',evl_ks)
from matplotlib import pyplot as plt
plt.plot(fpr_lr_train,tpr_lr_train,label = 'train LR')
plt.plot(fpr_lr,tpr_lr,label = 'evl LR')
plt.plot([0,1],[0,1],'k--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC Curve')
plt.legend(loc = 'best')
plt.show()
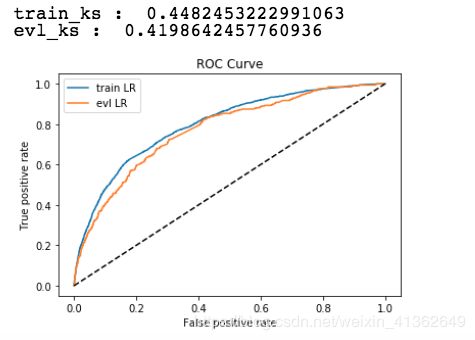
train_ks : 0.4859866821876423
evl_ks : 0.44085108654818894可以看到,最终跨时间验证集上,是有3.5个百分点的提升的。而训练集上提升了5个百分点,较为符合预期,过拟合的风险不是很大。