深度学习：梯度下降优化算法

1、梯度下降

梯度下降有许多变体，它们在用于计算目标函数梯度的数据量上存在差别。

---

1.1、Batch 梯度下降

$Batch$ 梯度下降计算整个训练集的成本函数相对参数 $\theta$ 的梯度。
$${\theta }^{t+1}={\theta }^t-\eta \cdot {\nabla }_{\theta }J({\theta }^t)\text{\hspace{1em}(1)}$$
由于每执行一次参数更新，需要计算整个数据集的梯度，所以 $Batch$ 梯度下降速度非常慢，而且在数据集很大的情况下会占用很多内存。当添加新样本时，该方法不适合在线更新模型。
但是，$Batch$ 梯度下降能够保证收敛到凸误差曲面的全局最小值，和非凸曲面的局部极小值。

---

1.2、随机梯度下降（SGD）

随机梯度下降为每个训练样本（$x_i$）和标签（$y_i$）执行参数更新。
$${\theta }^{t+1}={\theta }^t-\eta \cdot {\nabla }_{\theta }J\left({\theta }^t;x_i;y_i\right)\text{\hspace{1em}(2)}$$
$Batch$ 梯度下降对大数据集执行冗余计算，因为它在每个参数更新前重新计算相似样本梯度。$SGD$ 一次只执行一个样本上的更新来消除这种冗余。因此它通常更快，而且可以用于在线学习。$SGD$ 以很大的方差执行频繁的更新，导致目标函数剧烈波动，如图 $1$。

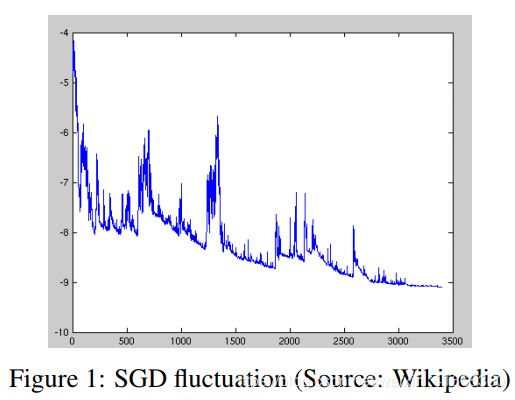
$Batch$ 梯度下降能够将参数更新到极小值。$SGD$ 的波动性一方面使它能够跳转到新的、可能更好的局部极小值，另一方面，这使收敛到精确的最小值变得复杂，因为 $SGD$ 会在最小值附近振荡。但是，当缓慢减小学习率时，$SGD$ 表现出与 $Batch$ 梯度下降相同的收敛性，几乎确定收敛到非凸优化的局部最小值和凸优化的全局最小值。

---

1.3、Mini-batch 梯度下降

$Mini-batch$ 梯度下降对两种方法进行折中，实现了最佳效果，并为每一个 $mini-batch$ 的 $n$ 个样本执行一次更新。
$${\theta }^{t+1}={\theta }^t-\eta \cdot {\nabla }_{\theta }J\left({\theta }^t;x_{(i:i+n)};y_{(i:i+n)}\right)\text{\hspace{1em}(3)}$$
这种方法可以：

1. 减小参数更新的方差，使收敛过程更稳定
2. 利用常见的深度学习库的高度优化的矩阵计算方法，高效计算 $mini-batch$ 梯度

训练神经网络时，通常采用 $mini-batch$ 梯度下降算法，但是使用 $SGD$ 这一术语。然而，普通的 $mini-batch$ 梯度下降不能保证好的收敛性，而且有以下问题需要解决：

1. 选择合适的学习率很困难。学习率太小会导致收敛速度过慢，学习率太大会阻碍收敛，导致损失函数在最小值附近波动，甚至发散。
2. 学习率 $schedules$ 尝试调整训练时的学习率，比如退火，即根据预定义的 $schedules$ 或者当迭代之间的目标变化低于某一阈值时，减小学习率。但是，$schedules$ 或者阈值必须预定义，因此无法适应数据集特征。
3. 所有参数更新使用相同学习率。如果数据是稀疏的，而且特征频率差异较大，那么我们不想同等程度更新所有参数，而是对较少出现的特征执行更大的更新。
4. 最小化高度非凸误差函数的另一个关键挑战是避免陷入许多次优局部极小。$Dauphin$ 等人认为，造成这一困难的原因不是局部极小值，而是鞍点，即在一个维度上坡度增加，另一维度上坡度减小。$SGD$ 在这些鞍点处很难逃脱，因为在所有维度上的梯度都接近于 $0$。

---

2、梯度下降优化算法

2.1、Momentum

$SGD$ 很难摆脱沟壑，即曲面的曲线在一个维度比另一维度更平稳，这通常是在局部最优附近。在这些场景下，$SGD$ 在峡谷的斜坡上振荡，沿着底部向局部最优方向前进的过程中徘徊不前，如图 $2a$ 所示。

$Momentum$ 有助于加速相关方向的梯度下降，并抑制振荡，如图 $2b$ 所示。它通过将之前的更新向量的 $\gamma$ 倍加到当前更新向量来实现这一点。
$$\begin{array}{rl}{v}^t& =\gamma v^{t-1}+\eta {\nabla }_{\theta }J({\theta }^t)\\ {\theta }^{t+1}& ={\theta }^t-v^t\end{array}\text{\hspace{1em}(4)}$$
动量项 $\gamma$ 通常设为 $0.9$。
对于梯度指向相同方向的维度 $momentum$ 项增加，对于梯度方向改变的维度，减少更新。这样就能实现更快地收敛，并减少震荡。

---

2.2、Nesterov 加速梯度

$NAG$ 是一种给出预见性动量项的方法。由于已知使用动量项 $\gamma v^{t-1}$ 来更新参数，因此计算 ${\theta }^t-\gamma v^{t-1}$ 给出了参数下一个位置的近似。这样做的好处是算法可以提前知道梯度方向发生改变，并相应地减小更新步长，从而加速收敛。
$$\begin{array}{rl}{v}^t& =\gamma v^{t-1}+\eta {\nabla }_{\theta }J\left({\theta }^t-\gamma v^{t-1}\right)\\ {\theta }^{t+1}& ={\theta }^t-v^t\end{array}\text{\hspace{1em}(5)}$$
将 $\gamma$ 设为 $0.9$。$Momentum$ 首先计算当前梯度（图 $3$ 小蓝色向量）然后在更新的累积梯度方向上前进一大步（大蓝色向量），$NAG$ 首先在之前累积的梯度方向进行大的跳跃（棕色向量），测量梯度然后进行校正（绿色向量）。这一预见性更新防止了参数更新过快并提升了响应能力，极大提升了 $RNN$ 在许多任务上的性能。

既然能够根据误差函数调整更新并相应加快 $SGD$ 速度，我们也希望根据每个参数的重要性来决定更新参数的程度。

$Keras$ 中调用相关优化器方法

keras.optimizers.SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False)
"""
: lr: 学习率 >= 0的浮点数
: momentum: >= 0的浮点数，在相关方向加速 SGD 并抑制震荡
: decay:  >= 0的浮点数，学习率随着更新过程衰减
: nesterov: 布尔值，是否应用 Nesterov 动量，一般用于 RNN
"""

---

2.3、Adagrad

$Adagrad$ 是一种基于梯度的优化算法，它使学习率适应于参数，对低频参数执行更大的更新，对高频参数执行更小的更新。因此，它非常适合处理稀疏数据。$Adagrad$ 极大地提升了 $SGD$ 的鲁棒性。

过去，执行一次更新，每个参数使用相同的学习率 $\eta$。$Adagrad$ 在每次更新时，不同的参数的学习率不同。单个参数 ${\theta }_i$ 的更新如下：
$$g_i^t={\nabla }_{{\theta }^t}J\left({\theta }_i^t\right)\text{\hspace{1em}(6)}$$
$${\theta }_i^{t+1}={\theta }_i^t-\frac{\eta }{\sqrt{G_{ii}^t+ϵ}}\cdot g_i^t\text{\hspace{1em}(7)}$$
所有参数更新的矩阵形式为：
$${\theta }^{(t+1)}={\theta }^{(t)}-\eta {\left(G^t\right)}^{-1}\odot {\nabla }_{{\theta }^t}J\left({\theta }^t\right)\text{\hspace{1em}(8)}$$
其中：
$$G^t=\left[\begin{array}{cccc}\sqrt{\sum _{\tau =1}^t{g}_1^{\tau }+ϵ}& 0& \cdots & 0\\ 0& \sqrt{\sum _{\tau =1}^t{g}_2^{\tau }+ϵ}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \sqrt{\sum _{\tau =1}^t{g}_d^{\tau }+ϵ}\end{array}\right]$$
$G^t$ 是一个对角矩阵，每一个对角线元素为该位置对应参数的前 $t$ 次更新中梯度的平方和。$ϵ$ 为平滑参数，避免分母为 $0$（通常为 $1e-8$）。有趣的是，如果没有平方根运算，该算法效果更差。

$Adagrad$ 主要的优点是它不需要手动调整学习率，通常使用默认值 $0.01$。

$Adagrad$ 主要的缺点是，它在分母中积累了平方梯度：由于增加的每一项都是正的，训练过程中累计和不断增加。这相应地导致学习率减小，最终趋于无穷小，此时算法难以继续学习。

$Keras$ 调用优化器方法：

keras.optimizers.Adagrad(lr=0.01, epsilon=1e-06)
"""
lr：大于0的浮点数，学习率
epsilon：大于0的小浮点数，防止除0错误
"""

---

2.4、Adadelta

$Adadelta$ 是 $Adagrad$ 的延伸。取代累加之前所有梯度平方，$Adadelta$ 累加之前固定范围 $w$ 内的梯度。

梯度和被递归地定义为所有过去平方梯度衰减的平均值，而不是无效地存储 $w$ 个先前的平方梯度。在时间步 $t$ 时运行平均 $E[g^2{]}_t$，仅依赖于过去的均值和当前的梯度。：
$$E{\left[g^2\right]}_t=\gamma E{\left[g^2\right]}_{t-1}+(1-\gamma )g_t^2\text{\hspace{1em}(10)}$$
将 $\gamma$ 设为与动量项类似的值，约为 $0.9$。为清晰起见，根据参数更新向量 $\Delta {\theta }_t$ 重写 $SGD$ 更新。
$$\begin{array}{rl}\Delta {\theta }_t& =-\eta \cdot g_{t,i}\\ {\theta }_{t+1}& ={\theta }_t+\Delta {\theta }_t\end{array}\text{\hspace{1em}(11)}$$
$Adagrad$ 的参数更新向量表示为：
$$\Delta {\theta }_t=-\frac{\eta }{\sqrt{G_t+ϵ}}\odot g_t\text{\hspace{1em}(12)}$$
现在只需要将对角矩阵 $G_t$ 替换为过去平方梯度衰减的平均值
$$\Delta {\theta }_t=-\frac{\eta }{\sqrt{E{\left[g^2\right]}_t+ϵ}}{g}_t\text{\hspace{1em}(13)}$$
由于分母只是梯度的均方根（$RMS$）误差准则，可以用短期准则来代替它
$$\Delta {\theta }_t=-\frac{\eta }{RMS[g{]}_t}{g}_t\text{\hspace{1em}(14)}$$
作者指出，此更新中的单位（以及 $SGD$、$Momentum$ 或 $Adagrad$ 中的单位）不匹配，即更新应该具有与参数相同的假设单位。为了实现这一点，他们首先定义了另一个指数衰减平均值，这次不是平方梯度，而是平方参数更新：
$$E{\left[\Delta {\theta }^2\right]}_t=\gamma E{\left[\Delta {\theta }^2\right]}_{t-1}+(1-\gamma )\Delta {\theta }_t^2\text{\hspace{1em}(15)}$$
因此，参数更新的均方误差为：
$$RMS[\Delta \theta {]}_t=\sqrt{E{\left[\Delta {\theta }^2\right]}_t+ϵ}\text{\hspace{1em}(16)}$$
由于 $RMS[\Delta \theta {]}_t$ 未知，用直到前一步参数更新的 $RMS$ 逼近它。用 $RMS[\Delta \theta {]}_{t-1}$ 替换上一个更新规则中的学习率，最终得到 $Adadelta$ 更新规则：
$$\begin{array}{rl}\Delta {\theta }_t& =-\frac{RMS[\Delta \theta {]}_{t-1}}{RMS[g{]}_t}{g}_t\\ {\theta }_{t+1}& ={\theta }_t+\Delta {\theta }_t\end{array}\text{\hspace{1em}(17)}$$
使用 $Adadelta$，甚至不需要设置默认学习率，因为它已经被从更新规则中删除了。

$Keras$ 调用优化器方法：

keras.optimizers.Adadelta(lr=1.0, rho=0.95, epsilon=1e-06)
"""
lr：大于0的浮点数，学习率
rho：大于0的浮点数
epsilon：大于0的小浮点数，防止除0错误
"""

---

2.5、RMSprop

$RMSprop$ 是一种自适应学习率方法。它与 $Adadelta$ 均用于解决 $Adagrad$ 学习率急剧下降的问题。事实上，$RMSprop$ 与 $Adadelta$ 的第一个更新向量相同。
$$\begin{array}{rl}E{\left[g^2\right]}_t& =0.9E{\left[g^2\right]}_{t-1}+0.1g_t^2\\ {\theta }_{t+1}& ={\theta }_t-\frac{\eta }{\sqrt{E{\left[g^2\right]}_t+ϵ}}{g}_t\end{array}\text{\hspace{1em}(18)}$$
此外，$RMSprop$ 将学习率除以指数衰减的平方梯度的均值。$\gamma$ 最好设置为 $0.9$，学习率 $\eta$ 通常为 $0.001$。

$Keras$ 调用优化器方法：

keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-06)
"""
lr：大于0的浮点数，学习率
rho：大于0的浮点数
epsilon：大于0的小浮点数，防止除0错误
"""

---

2.6、Adam

$AdaptiveMomentEstimation(Adam)$ 是另一种计算每个参数自适应学习率的方法。除了存储指数衰减的平方梯度均值 $v_t$，它还保留了类似于 $momentum$ 的，指数衰减的梯度均值 $m_t$。
$$\begin{array}{rl}{m}_t& ={\beta }_1{m}_{t-1}+\left(1-{\beta }_1\right)g_t\\ v_t& ={\beta }_2{v}_{t-1}+\left(1-{\beta }_2\right)g_t^2\end{array}\text{\hspace{1em}(19)}$$
$m_t$ 和 $v_t$ 分别为梯度的一阶矩（均值）和二阶矩估计，这是该方法名字的由来。当 $m_t$ 和 $v_t$ 被初始化为零向量时，在初始时间步，它们都偏向于 $0$，特别当衰变率很小时更是如此（即，${\beta }_1$ 和 ${\beta }_2$ 接近于 $1$）。

通过计算一阶矩和二阶矩估计偏差修正来抵消偏差。
$$\begin{array}{rl}{\hat{m}}_t& =\frac{m_t}{1-{\beta }_1^t}\\ {\hat{v}}_t& =\frac{v_t}{1-{\beta }_2^t}\end{array}\text{\hspace{1em}(20)}$$
$Adam$ 更新规则如下：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t\text{\hspace{1em}(21)}$$
${\beta }_1$ 默认为 $0.9$，${\beta }_2$ 默认为 $0.999$，$ϵ$ 默认为 $10^{-8}$。实验表明，相比于其他自适应算法，$Adam$ 效果更好。

$Keras$ 调用优化器方法：

keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08)
"""
lr：大于0的浮点数，学习率
beta_1/beta_2：浮点数， 0

---

2.7、AdaMax

$Adam$ 中的 $v_t$ 因子反向缩放之前梯度的 ${\ell }_2$ 范数和当前梯度 $|g_t{|}^2$：
$$v_t={\beta }_2{v}_{t-1}+\left(1-{\beta }_2\right){\left|g_t\right|}^2\text{\hspace{1em}(22)}$$
这里将其改为 ${\ell }_p$ 范数，同时 ${\beta }_2$ 变为 ${\beta }_2^p$
$$v_t={\beta }_2^p{v}_{t-1}+\left(1-{\beta }_2^p\right){\left|g_t\right|}^p\text{\hspace{1em}(23)}$$
大 $p$ 值范数通常在数值上不稳定，因此实践中 ${\ell }_1$ 和 ${\ell }_2$ 范数比较常见。然而，${\ell }_{\infty }$ 通常表现更稳定。因此作者提出了 $AdaMax$，并证明了具有 ${\ell }_{\infty }$ 的 $v_t$ 收敛到更稳定的值。为避免与 $adam$ 混淆，这里使用 $u_t$ 表示受无穷范数约束的 $v_t$。
$$\begin{array}{rl}{u}_t& ={\beta }_2^{\infty }{v}_{t-1}+\left(1-{\beta }_2^{\infty }\right){\left|g_t\right|}^{\infty }\\ & =\max \left({\beta }_2\cdot v_{t-1},\left|g_t\right|\right)\end{array}\text{\hspace{1em}(24)}$$
通过将 $\sqrt{{\hat{v}}_t}+ϵ$ 替换为 $u_t$ 来获取 $Adam$ 更新规则：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{u_t}{\hat{m}}_t\text{\hspace{1em}(25)}$$
由于 $u_t$ 依赖于 $max$ 运算，所以不像 $Adam$ 中的 $m_t$ 和 $v_t$ 容易偏向于 $0$，因此不需要计算 $u_t$ 的校正。默认值：$\eta =0.002,{\beta }_1=0.9,$ ${\beta }_2=0.999$。

$Keras$ 调用优化器方法：

keras.optimizers.Adamax(lr=0.002, beta_1=0.9, beta_2=0.999, epsilon=1e-08)
"""
lr：大于0的浮点数，学习率
beta_1/beta_2：浮点数， 0

---

2.8、Nadam

$Adam$ 可以看作 $RMSprop$ 和 $momentum$ 的结合：$RMSprop$ 贡献指数衰减的之前梯度平方的均值 $v_t$，$momentum$ 计算指数衰减的之前梯度的均值 $m_t$。$Nesterov$ 加速梯度优于普通的 $momentum$。

$Nadam(Nesterov-acceleratedAdaptiveMomentEstimation)$ 将 $Adam$ 和 $NAG$ 结合起来。为了将 $NAG$ 结合到 $Adam$ 需要修改动量项 $m_t$

当前动量更新规则为：
$$\begin{array}{rl}{g}_t& ={\nabla }_{{\theta }_t}J\left({\theta }_t\right)\\ m_t& =\gamma m_{t-1}+\eta g_t\\ {\theta }_{t+1}& ={\theta }_t-m_t\end{array}\text{\hspace{1em}(26)}$$
将第二式带入第三式：
$${\theta }_{t+1}={\theta }_t-\left(\gamma m_{t-1}+\eta g_t\right)\text{\hspace{1em}(27)}$$
$NAG$ 在计算梯度之前，使用动量步长更新参数，从而实现更精确的参数更新。
$$\begin{array}{rl}{g}_t& ={\nabla }_{{\theta }_t}J\left({\theta }_t-\gamma m_{t-1}\right)\\ m_t& =\gamma m_{t-1}+\eta g_t\\ {\theta }_{t+1}& ={\theta }_t-m_t\end{array}\text{\hspace{1em}(28)}$$
$Dozat$ 提出修改 $NAG$：不再使用两次动量—一次用于更新梯度，另一次用于更新参数。直接使用前瞻性动量向量更新当前参数。
$$\begin{array}{rl}{g}_t& ={\nabla }_{{\theta }_t}J\left({\theta }_t\right)\\ m_t& =\gamma m_{t-1}+\eta g_t\\ {\theta }_{t+1}& ={\theta }_t-\left(\gamma m_t+\eta g_t\right)\end{array}\text{\hspace{1em}(29)}$$
注意与 $27$ 的区别。为了给 $Adam$ 增加 $Nesterov$ 动量，使用当前动量向量代替之前的动量向量。$Adam$ 更新规则如下：
$$\begin{array}{rl}{m}_t& ={\beta }_1{m}_{t-1}+\left(1-{\beta }_1\right)g_t\\ {\hat{m}}_t& =\frac{m_t}{1-{\beta }_1^t}\\ {\theta }_{t+1}& ={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t\end{array}\text{\hspace{1em}(30)}$$
将前两式代入第三式得：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}\left(\frac{{\beta }_1{m}_{t-1}}{1-{\beta }_1^t}+\frac{\left(1-{\beta }_1\right)g_t}{1-{\beta }_1^t}\right)\text{\hspace{1em}(31)}$$
由于 $\frac{{\beta }_1{m}_{t-1}}{1-{\beta }_1^t}$ 是上一步动量向量的偏移修正项，可以将它用 ${\hat{m}}_{t-1}$ 替代：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}\left({\beta }_1{\hat{m}}_{t-1}+\frac{\left(1-{\beta }_1\right)g_t}{1-{\beta }_1^t}\right)\text{\hspace{1em}(32)}$$
看起来和等式 $27$ 类似，我们将仿照等式 $29$ 的做法添加 $Nesterov$ 动量。将上一步动量向量的偏移估计 ${\hat{m}}_{t-1}$ 用当前动量向量的偏移估计替代：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}\left({\beta }_1{\hat{m}}_t+\frac{\left(1-{\beta }_1\right)g_t}{1-{\beta }_1^t}\right)\text{\hspace{1em}(33)}$$

$Keras$ 调用优化器方法：

keras.optimizers.Nadam(lr=0.002, beta_1=0.9, beta_2=0.999, 
						epsilon=1e-08, schedule_decay=0.004)
"""
lr：大于0的浮点数，学习率
beta_1/beta_2：浮点数， 0

---

2.9、各优化方法收敛速度的比较

从网上找到两张图，可以清晰对各种优化方法进行比较

2.10、如何选择优化方法

1. 如果数据是稀疏的，就选择自适应学习率方法。还可以省去调节学习率的麻烦
2. $RMSprop$ 是 $Adagrad$ 的扩展，解决学习率急剧消失的问题
3. $Adadelta$ 和 $RMSprop$ 相同，只不过在更新规则的分子上使用了参数更新均方根
4. $Adam$ 在 $RMSprop$ 的基础上使用了偏移校正和动量
5. $RMSprop$、$Adadelta$ 和 $Adam$ 是相似的算法，在类似的情况的下做的很好。优化快要结束时，梯度变得越来越稀疏，偏移校正使 $Adam$ 略微超过 $RMSprop$。目前来说，$Adam$ 可能是整体优化的最佳选择。
6. 训练较深较复杂的网络时，推荐使用学习率自适应的优化方法。

---

3、参考

An overview of gradient descent optimization
algorithms