霍夫变换 Hough Transfom（附Matlab实验代码）
前言
在学习过程中，我发现许多文章一上来就介绍Hough变换的特点和数学原理，却忽视了Hough变换的使用场景（在边缘检测之后使用），因此很容易让人捉摸不透。在本文中，大家可以关注一下这一点。
一、Hough变换使用场景
我们先通过边缘检测，得到了幅值超过某个阈值的像素集合，即边缘像素。我们想知道，这些边缘像素是否连成直线，即验证这些边缘像素是否在某直线上。为此，我们可以采用Hough变换。
二、Hough变换用于直线边缘检测
我们猜测：边缘像素点A：
和B：
在一条直线上：
。我们希望通过Hough变换，验证我们的猜测。
注意，我们往往不知道直线的具体参数，即我们只能先假设存在边缘直线
，然后再找出斜率和纵坐标的具体值。
一句话：我们现在只有边缘像素点集合
，任务是：一，验证是否在直线上；二，找出k和q的具体值。
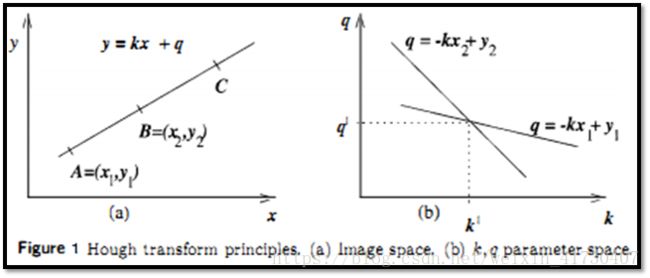
继续。我们把点A和点B代入方程中，经过变形，我们可以得到两条直线方程：
如上方右图所示。注意，此时k和q是变量，因此两条直线位于参数空间中。
如果A和B确实是上的两个点，那么这两条直线方程就一定会经过
点！并且，这个交点是唯一的！因为，A和B只能唯一确定一条直线！
总结、拓展：
1、我们把每一个样本坐标
，代入我们猜测的直线方程中，都能得到一条直线
。
2、这一条直线上包括无穷多个离散的
坐标对。
3、因此，由边缘像素点集
，可以计算得到多条直线，每一条直线都有对应的坐标集合。
4、如果确实在同一条直线上，那么直线簇一定会交于同一点，交点坐标就是。
5、具体方法是：我们选择若干可能的k和若干可能的q，作为备选参数对。若某个离散坐标对
恰好出现在某个备选参数对附近，那么该参数对就计数+1；显然，的计数次数是最多的。
出现次数可以构成一个矩阵A(k,q)，我们称之为累次数组，非常形象。进一步说：
如果累次数组在某处存在峰值，那么就说明：原图像空间可能存在直线边缘，并且峰值就是处于上的边缘像素点的数目。
显然，由于是基于统计峰值得到的结果，因此Hough变换对图像中直线的残缺部分、噪声以及其它共存的非直线结构不敏感。
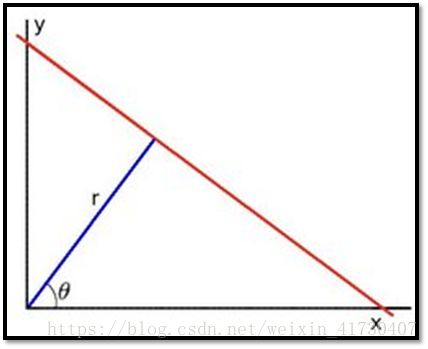
在检测垂直线条和参数非线性离散化时，斜率表示会遇到困难。为此，我们常把直线表示为：
可以证明以下结论：
1) 图像空间中的一个点，对应空间中的一条正弦曲线：
和差化积可证。
2) 图像空间中的一条直线，对应空间中存在一个公共点的一簇曲线。
公共点为
，对应直线就是：
基于上述结论，直线检测过程同理：
1) 边缘检测，得到若干边缘像素。
2) 预估并规定有限、离散的集合，得到累计数组。
3) 每一个都可以得到一条正弦曲线；如果曲线经过某参数对所在区域，就计数+1。
4) 统计累计数组的峰值。如果在某参数对处存在峰值C，则可能存在直线边缘：
且直线上的边缘像素个数为C。
三、Hough变换用于圆边缘检测
假设在原始空间中，存在一个圆心为
的圆：
该圆上的点组成组成一个集合。
假设通过边缘检测，其中若干离散点被检测为边缘像素点。Hough变换：
1) 根据和假设圆方程
，计算出轨迹：
2) 在事先预测的、可能的参数对
集合中，如果轨迹经过某参数对附近，那么该参数对计数+1。
3) 统计累计数组
的峰值C。
显然，由于这些点都满足：
因此圆轨迹一定都经过。即一定是统计峰值点，并且原图像空间中，处在圆上的边缘像素点数目为C。
当然，如果有多个峰值点，就有多个目标。在这里就不详述了。
四、检测圆实验
实验所用圆图片和代码下载：https://download.csdn.net/download/weixin_41730407/10467900
实验思想见代码注释。
实验结果：（高斯噪声；Roberts算子）
实验代码：
function CurveDetectionbyHough
%~~~~~~~~~~~~~~~~~~~~~~~第四次数图实验说明~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
% 1、实验最初，需要选择其中一种加噪方式。
% 2、边缘检测后，需要观察、选择其中一个算子继续处理，以减小程序耗时。
% 3、简化实验参数range、delta、min都是预实验得到的最佳参数，不建议更改。
% 4、坐标系：→x坐标
% ↓ y坐标
% 原点为(1,1)
% 2018-5-22 by XING
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
clear;close all;clc;
fprintf('**********************加噪图像曲线检测实验**********************\n');
I = im2double(rgb2gray(imread('houghorg.bmp')));
fprintf('\n~~~~~~~~~~~~~~~Part0: 图像加噪~~~~~~~~~~~~~~~\n');
fprintf(' 选择添加噪声类型:\n');
option=input(' Gaussian(1) or Salt(2):\n ');
if(option==1)
I_noised=imnoise(I,'gaussian',1e-3);
else
I_noised=imnoise(I,'salt & pepper',1e-3);
end
[height,width] = size(I_noised);
figure;
subplot(1,2,1),imshow(I);
title('\fontsize{20}Original');
subplot(1,2,2),imshow(I_noised);
title('\fontsize{20}Noised');
fprintf('\n~~~~~~~~~~~~Part1: 图像滤波和边缘检测~~~~~~~~~~~~');
%% Median Filtering
m=9;
I_smooth = medfilt2(I_noised,[m m]);% 9x9中值滤波
%% Edge Detection
% Roberts
IRoberts=edge(I_smooth,'Roberts');
figure;
subplot(1,3,1),imshow(IRoberts);
title('\fontsize{20}Roberts');
% Sobel
ISobel=edge(I_smooth,'Sobel');
subplot(1,3,2),imshow(ISobel);
title('\fontsize{20}Sobel');
% Laplacian
ILap=edge(I_smooth,'log');
subplot(1,3,3),imshow(ILap);
title('\fontsize{20}Laplacian');
suptitle('\fontsize{20}Edge Detection');
fprintf('\n 对比发现，Roberts边缘检测噪点最少，后续计算量最小，因此建议选择。');
fprintf('\n 选择算子类型:\n');
option=input(' Roberts(1) or Sobel(2) or Laplacian(3):\n ');
close all;
if(option==1)
IEdge=IRoberts;
elseif(option==2)
IEdge=ISobel;
else
IEdge=ILap;
end
figure;
subplot(1,3,1),imshow(I);
title('\fontsize{20}Original');
subplot(1,3,2),imshow(I_noised);
title('\fontsize{20}Noised');
subplot(1,3,3),imshow(IEdge);
title('\fontsize{20}Edge Detection')
% 将边缘点坐标放在数组X和Y中，以便后续操作。
totalnum=sum(sum(IEdge));
X=zeros(1,totalnum);
Y=zeros(1,totalnum);
k=0;
for x=1:width
for y=1:height
if IEdge(y,x)% 是轨迹点 一定要注意是y（行） x（列）
k=k+1;
X(k)=x;
Y(k)=y;
if k==totalnum
break;
end
end
end
if k==totalnum
break;
end
end
fprintf('\n~~~~~~~~Part2: 圆检测和重建叠加（Hough变换）~~~~~~~~');
%% Curve Detection by Hough
% assume that (x-a_0)^2+(y-b_0)^2=r^2
% parameter equation: (a-x_i)^2+(b-y_i)^2=r^2
% 坐标系：→x坐标
% ↓ y坐标
% 原点为(1,1)
fprintf(' \n 程序已发现 %d 个边缘轨迹点，对应 %d 个参数圆。\n',totalnum,totalnum);
fprintf(' 警告：\n');
fprintf(' 如果把412x315个点都当作潜在圆心点进行计算，耗时将很长很长。\n');
fprintf('\n 通过观察图像，我们可以缩小计算范围：\n');
fprintf(' 1、圆心位于(230,175)左右，圆心计算范围可缩小至附近20x20区域；\n');
fprintf(' 这样只需要统计400个点，计算量较小；\n');
apro_min=220;
bpro_min=165;
range=20;
APRO=(apro_min:apro_min+range-1)';
BPRO=(bpro_min:bpro_min+range-1)';
fprintf(' 2、半径长度在95左右，半径计算范围可缩小至85:105。\n');
r_min=85;
range2=20;
fprintf('\n Program paused. Press enter to continue.\n');
pause;
% 求解二元隐函数非常非常复杂。我们反过来，在20x20方阵内，逐点验证是否可能为参数圆的轨迹点。
% 误差delta可调，在正负delta内都算有效解。预实验建议值为25。
% 预实验说明，当delta较小时，最大频次很小，统计误差很大。
delta=50;
r_step=0.5;
count=0;
A_Maxpro=[];
B_Maxpro=[];
RMAXNUM=[];
tic;
for r=r_min:r_step:r_min+range2 % 半径也取决于统计峰值
count=count+1;
Frequency=zeros(range,range);% 该20x20方阵点出现在参数圆轨迹中的次数
for k=1:totalnum %逐个样本
left=repmat(((APRO-X(k)).^2)',range,1)+repmat((BPRO-Y(k)).^2,1,range);
right=r^2;
Difference=round(left-right);
ISSOLUTION=(Difference-delta);
Frequency=Frequency+ISSOLUTION;
end
maxFrequency=max(Frequency(:));% 找出统计峰值
[b_maxpro,a_maxpro]=find(Frequency==max(Frequency(:)));% 具有统计峰值，意味着该点最有可能是圆心(a_0,b_0)
A_Maxpro=[A_Maxpro;a_maxpro];
B_Maxpro=[B_Maxpro;b_maxpro];
RMAXNUM=[RMAXNUM;maxFrequency];
% 以上三者，记录的是在某一个r下的统计峰值和圆心坐标
end
final_max_Rposition=find(RMAXNUM==max(RMAXNUM));
R=r_min+(final_max_Rposition-1)*r_step;% 在所有r下的最大峰值对应的半径r
final_a_pro=A_Maxpro(final_max_Rposition)+apro_min;
final_b_pro=B_Maxpro(final_max_Rposition)+bpro_min;
fprintf(' \n Hough圆形边缘检测结果：Centre=(%d,%d)，Radius=%.1f。\n',final_a_pro,final_b_pro,R);
fprintf(' Hough检测耗时：%.3f s。\n', toc);
%% Image Superposition
% Restruction
IRe=zeros(height,width);% 再次注意先行数后列数
delta2=1;
for m=1:height
for n=1:width
r_cal=sqrt((n-final_a_pro)^2+(m-final_b_pro)^2);
if (r_calR-delta2)
IRe(m,n)=1;
end
end
end
IRe=IRe+IEdge;
close all;
figure;
subplot(2,2,1),imshow(I);
title('\fontsize{20}Original');
subplot(2,2,2),imshow(I_noised);
title('\fontsize{20}Noised');
subplot(2,2,3),imshow(IEdge);
title('\fontsize{20}Edge Detected');
subplot(2,2,4),imshow(IRe);
title('\fontsize{20}Reconstructed');
fprintf('\n**********************第四次数图实验结束**********************\n');
fprintf(' Written by XING\n');
fprintf(' 2018-5-22 Beijing\n');
end