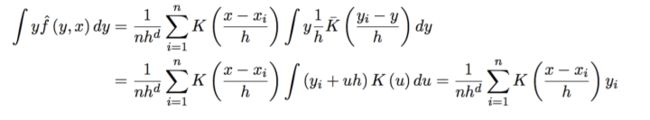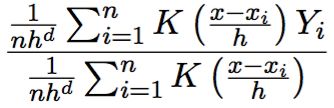非参数估计 -核密度估计(KDE)

 

元学习论文总结||小样本学习论文总结

2017-2019年计算机视觉顶会文章收录 AAAI2017-2019 CVPR2017-2019 ECCV2018 ICCV2017-2019 ICLR2017-2019 NIPS2017-2019

 

---

核密度估计其实是对直方图的一个自然拓展。

首先考虑一下密度函数的概念，很自然的可以想到，密度函数就是分布函数的一阶导数。那么当我们拿到一些数据的时候，是不是可以通过估计分布函数的一阶导数来估计密度函数呢？一个最简单而有效的估计分布函数的方法是所谓的「经验分布函数（empirical distribution function）」：

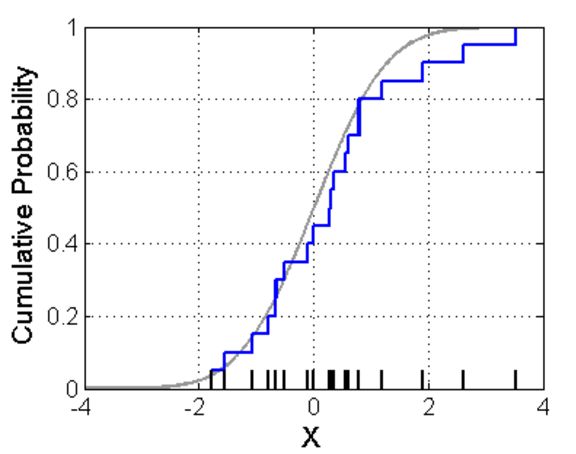
即，F(t)的估计为所有小于t的样本的概率。可以证明，这个估计是almost surely收敛的，有很好的统计性质。如果画下来，应该是下图蓝线的样子：

可是这个EDF不是可导的，不够光滑，因而不能通过对EDF的一阶导数算密度函数。那么如何估计密度函数呢？

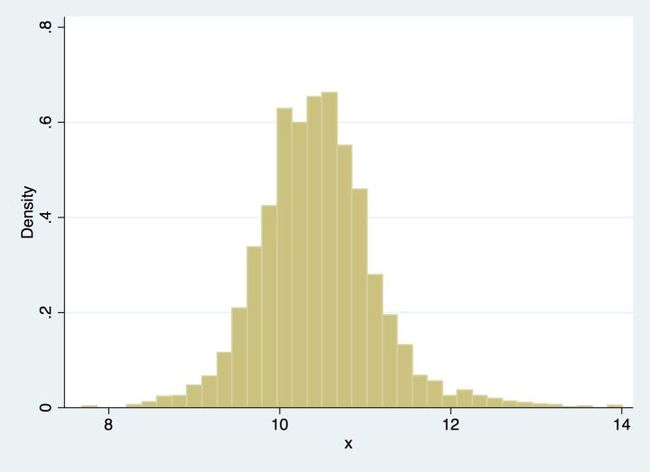
我们一般看密度的时候，会首先画一个直方图，像下图：

一个很自然的想法是，如果我们想知道X=x处的密度函数值，可以像直方图一样，选一个x附近的小区间，数一下在这个区间里面的点的个数，除以总个数，应该是一个比较好的估计。用数学语言来描述，如果你还记得导数的定义，密度函数可以写为：

我们把分布函数用上面的经验分布函数替代，那么上式分子上就是落在[x-h,x+h]区间的点的个数。我们可以把f(x)的估计写成：

那么一个很自然的问题来了，h该怎么选取呢？

 

给定样本容量N，h如果选的太大，肯定不符合h趋向于0的要求。h选的太小，那么用于估计f(x)的点实际上非常少。

这也就是非参数估计里面的bias-variance tradeoff：如果h太大，用于计算的点很多，可以减小方差，但是方法本质要求h→0，bias可能会比较大；如果h太小，bais小了，但是用于计算的点太少，方差又很大。

所以理论上存在一个最小化mean square error的一个h。h的选取应该取决于N，当N越大的时候，我们可以用一个比较小的h，因为较大的N保证了即使比较小的h也足以保证区间内有足够多的点用于计算概率密度。因而，我们通常要求当N→∞，h→0。比如，在这里可以推导出，最优的h应该是N的-1/5次方乘以一个常数，也就是。对于正态分布而言，可以计算出c=1.05×标准差。

另外，我们知道之前的经验分布函数每个点的收敛速度都是√N的，而这里，因为有h的存在（观察估计式，分母上是nh而非n，而nh=O(N^{-4/5})）。所以收敛速度比一般的参数收敛速度要慢很多。

上面的这个估计看起来还可以，但是还不够好，得到的密度函数不是光滑的。观察上面的估计式子，如果记，那么估计式可以写为：

密度函数的积分：

因而只要K的积分等于1，就能保证估计出来的密度函数积分等于1。

那么一个自然的想法是，我们是不是可以换其他的函数形式呢？比如其他的分布的密度函数作为K？

比如，我可以用标准正态分布的密度函数作为K，估计就变成了：

这个密度函数的估计就变得可导了，而且积分积起来等于1。直觉上，上式就是一个加权平均，离x越近的x_i其权重越高。而最开始的估计方式则是在区间内权重相等，区间外权重为0。

当然，这里还是有h的选取问题，其原理跟上面是一样的。也因此，一般我们会把h叫做「窗宽（bandwidth）」。关于窗宽的选择方法有很多，可以plug-in，也可以用cross-validation，具体就不做赘述了。

此外还可以扩展到多维，即

其中d为x的维数，K为多维的kernel，一般为d个一维kernel的乘积。

 

上面的蓝色线条就是kernel density的结果。

 

有了density的估计，可以更进一步，做非参数的回归。如果我们有：

其中u与x独立，可以得到：

其中分子（这里需要用到核函数K的对称性）：

最终就得到了非参数回归，或者核平滑（kernel smoothing）:

其中对于核函数K还有很多其他要求，以及高阶Kernel等等，就不一一介绍啦。感兴趣的可以参考Qi Li的书。

转载：

https://www.zhihu.com/question/27301358/answer/105267357?from=profile_answer_card 

参考：https://blog.csdn.net/unixtch/article/details/78556499