神经网络学习笔记（一) RBF径向基函数神经网络

RBF径向基函数神经网络

初学神经网络，以下为综合其他博主学习材料及本人理解所得。

一、径向基函数RBF

定义（Radial basis function——一种距离）

径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数。

标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。在神经网络结构中，可以作为全连接层和ReLU层的主要函数。

如何理解径向基函数与神经网络？

一些径向函数代表性的用到近似给定的函数，这种近似可以被解释成一个简单的神经网络。

径向基函数在支持向量机中也被用做核函数。

常见的径向基函数有：高斯函数，二次函数，逆二次函数等。

应用

构造神经网络的基本方法为假设某种过程是属于某种函数空间的函数，然后连接成神经网格，运行一段时间该网络的电势趋于最小达到某种动态的平衡，从而可以求出该函数，而选择径向基函数空间是一个比较简单的容易用神经网络实现的方法。

 

二、RBF神经网络的基本思想（从函数到函数的映射）

1. 用RBF作为隐单元的“基”构成隐含层空间，将输入矢量直接（不通过权映射）映射到隐空间。

2.当RBF的中心点确定后，映射关系也就确定。（中心点通常通过K-MEANS聚类获得）

3.隐含层空间到输出空间的映射是线性的。（其中的权值通过最小二乘法获得）

4.将低维度映射到高维度，使得线性不可分转化为线性可分。

三、RBF神经网络模型

RBF神经网络神经元结构

1.输入层为向量，维度为m，样本个数为n，传输函数为线性函数。

2.隐藏层与输入层全连接，层内无连接，隐藏层神经元个数与样本个数相等，也就是n，传输函数为径向基函数。

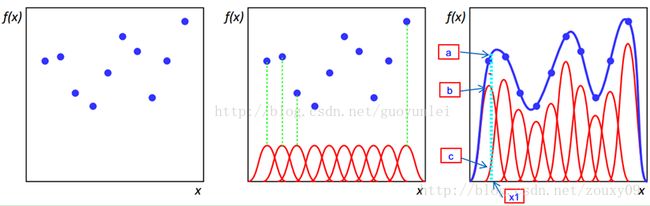
输入的X1-Xm为离散点，我们要得到平滑函数，即通过基函数对样本点附近的点做插值。

通常我们将基函数设为高斯函数。

高斯函数： exp（-d^2/(2*sigma^2)）;

sigma：平滑因子，又称为基函数的拓展函数或者宽度。平滑因子控制高斯函数的平滑度。当平滑因子较低时，高斯函数就会尖锐，也就是边缘点的权值会很小，导致过拟合。

距离d：距离d就是向量离每一个隐含层中心的距离，通常隐含层的中心对应每个节点，所以每个距离就是节点矩阵自身相对自身每个点的距离。距离表示着离节点越近，所受该节点的输出影响就越大。

四、径向基神经网络结构

总体表达：

通俗过程:

求输入样本和隐藏层点（中心点）的范数，得到范数后，将其带入径向基函数。

得到一个数值，再与之后的权值相乘加和，就得到了相应的输出。

 

五、RBF网络的学习算法

经过上面的学习，我们得到了该学习算法需要求解的参数

1.径向基函数的中心（隐含层中心点）

中心的选取主要有三个方法

（1)    固定中心法

（2）自组织选取中心法

（3）有监督选取中心法

常用K-means聚类方法求取基函数中心

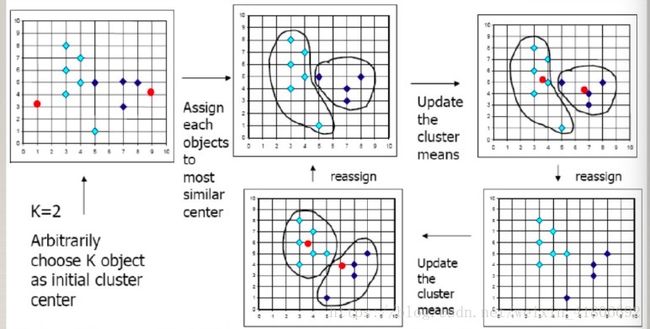
原理：算法首先随机选择K个对象，每个对象初始地代表了一族的平均值或中心。对剩余的每个对象根据其余各个族中心的距离，将它赋给最近的族，然后重新计算每个族的平均值。这个过程不断重复，知道准则函数收敛。

K-means算法过程图

2.方差（sigma)

上文已介绍。

3.隐含层到输出层的权值

通过最小二乘法求得。

下面从MATLAB实例中给出最小二乘法求权值的运用。

%给出变量
%实际数据
data=-9:1:8;
%测试数据
x=-9:.2:8;
%目标输出
label=[129,-32,-118,-138,-125,-97,-55,-23,-4,2,1,-31,-72,-121,-142,-174,-155,-77];
%sigma值
spread=2;
plot(data, label,'o');

%拟合这条曲线的权值
dis=dist(data',data);
gdis=exp(-dis.^2/spread);%gauss
G=[gdis,ones(length(data(1,:)),1)];%广义rbf网络 （加入一个恒为1的隐含层节点）
w=G\label';%最小二乘的矩阵求解

%测试所拟合的权值
chdis=dist(x',data);
chgdis=exp(-chdis.^2/spread);
chG=[chgdis,ones(length(x(1,:)),1)];
chy=chG*w;
plot(x,chy);

五、RBF网络学习算法的MATLAB实现

通过matlab自带的函数做RBF网络学习

1. newrb()  新建一个径向基神经网络

2.newrbe() 新建一个严格的径向基神经网络

3.newrnn() 新建一个广义回归径向基神经网络

4.newpnn() 新建一个概率径向神经网络

 

格式：net=newrb(P,T,GOAL,SPREAD,MN,DF)

P:输入向量

T：目标向量

SPREAD：径向基函数的分布密度，默认为1

MN：神经元的最大数目

DF：两次显示之间所添加的神经元数目

六、RBF网络学习算法的范例

例、建立一个径向基神经网络，对非线性函数y=sqrt(x)进行逼近，并作出网络的逼近误差曲线。

---

 %输入从0开始变化到5，每次变化幅度为0.1
 x=0:0.1:5;
y=sqrt(x);
 %建立一个目标误差为0，径向基函数的分布密度为0.5
 %隐含层神经元个数的最大值为20，每增加5个神经元显示一次结构
 net=newrb(x,y,0,0.5,20,5)

t=sim(net,x)

%作出误差函数

plot(x,y-t,'*-')