数据挖掘#特征工程（二）特征重要性及可解释性总结

在打比赛的时候一直贯穿的思考，大概就是判别各个特征的重要性。

在建立模型之前，特征重要性能够帮助训练模型，防止过拟合，提升模型的RUC效果。

建立模型之后，特征重要性能够增强模型（集成模型 非深度学习模型）的可解释性，帮助建立模型信任、做出现实意义上的决策。

建模前特征重要性判别

要构建数值型连续变量的监督学习模型，最重要的方面之一就是好好理解特征。观察一个模型的部分依赖图有助于理解模型的输出是如何随着每个特征变化而改变的。

1.featexp

一位名叫Abhay Pawar的小哥开发了一些特征工程和机器学习建模的标准方法。

• 特征理解
• 识别嘈杂特征
• 特征工程
• 特征重要性
• 特征调试
• 泄漏检测与理解
• 模型监控

特征理解

                                                     

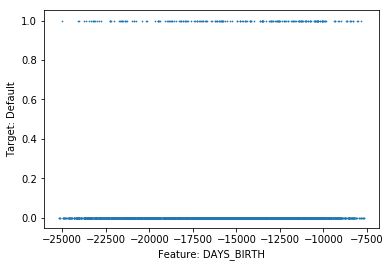
如果因变量 (分析目标) 是二分类数据，散点图就不太好用了，因为所有点不是0就是1。针对连续型变量，数据点太多的话，会让人很难理解目标和特征之间的关系。但是，用featexp可以做出更加友好的图像。

                            

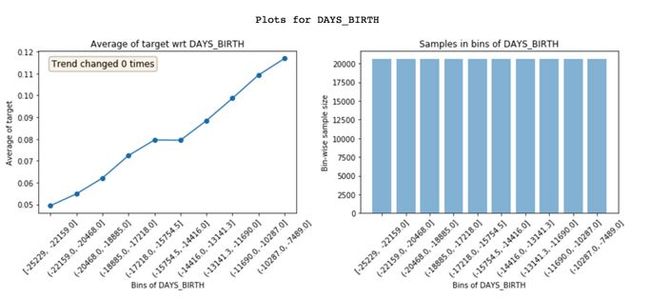
Featexp可以把一个数字特征，分成很多个样本量相等的区间（X轴）。然后，计算出目标的平均值 (Mean)，并绘制出左上方的图像。在这里，平均值代表违约率。图像告诉我们，年纪 (DAYS_BIRTH) 越大的人，违约率越低。

这非常合理的，因为年轻人通常更可能违约。这些图能够帮助我们理解客户的特征，以及这些特征是如何影响模型的。右上方的图像表示每个区间内的客户数量。

get_univariate_plots(data=data_train, target_col='target', features_list=data_train.columns[0:10], data_test=data_test)

识别嘈杂特征

嘈杂特征容易造成过拟合，分辨噪音一点也不容易。

在featexp里，你可以跑一下测试集或者验证集，然后对比训练集和测试集的特征趋势，从而找出嘈杂的特征。

       

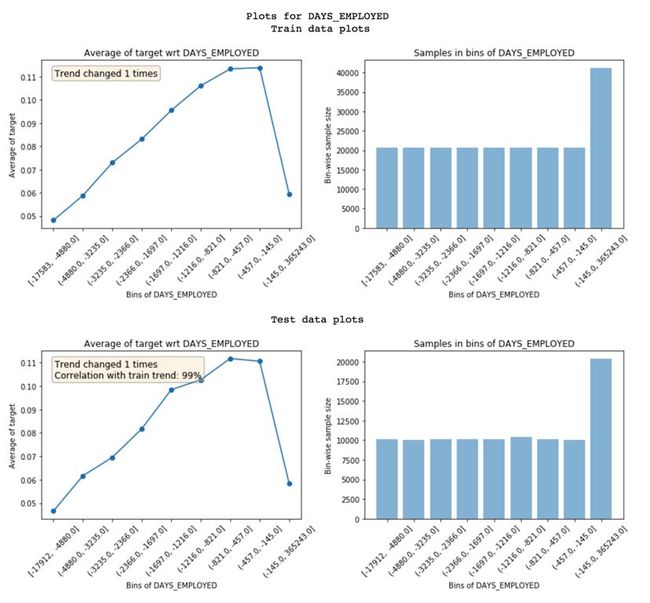
                                                                           训练集和测试集特征趋势的对比

为了衡量噪音影响程度，featexp会计算两个指标：

• 趋势相关性 (从测试绘图中可见) ：如果一个特征在训练集和验证集里面表现出来的趋势不一样，就有可能导致过拟合。这是因为，模型从训练集里学到的一些东西，在验证集中不适用。趋势相关性可以告诉我们训练集和验证集趋势的相似度，以及每个区间的平均值。上面这个例子中，两个数据集的相关性达到了99%。看起来噪音不是很严重！

• 趋势变化：有时候，趋势会发生突然变化和反复变化。这可能就参入噪音了，但也有可能是特定区间内有其他独特的特征对其产生了影响。如果出现这种情况，这个区间的违约率就没办法和其他区间直接对比了。

如果训练集和测试集没有相同的趋势：如两者相关性只有85%。有时候，可以选择丢掉这样的特征。

嘈杂特征的例子

抛弃相关性低的特征，这种做法在特征非常多、特征之间又充满相关性（95%以上的很多）的情况下比较适用。这样可以减少过拟合，避免信息丢失。不过，别把太多重要的特征都丢掉了；否则模型的预测效果可能会大打折扣。同时，你也不能用重要性来评价特征是否嘈杂，因为有些特征既非常重要，又嘈杂得不得了。

用与训练集不同时间段的数据来做测试集可能会比较好。这样就能看出来数据是不是随时间变化的了。

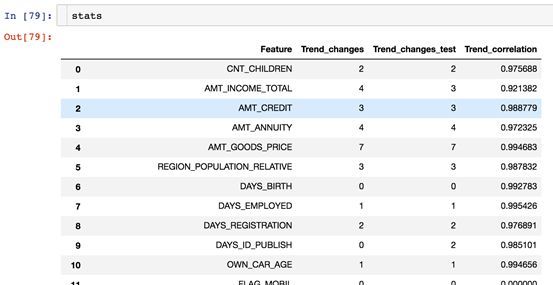
Featexp里有一个 get_trend_stats() 函数，可以返回一个数据框 (Dataframe) ，显示趋势相关性和趋势变化。

stats = get_trend_stats(data=data_train, target_col='target', data_test=data_test)

                                 

                                                                              get_trend_stats()返回的数据框

现在，可以试着去丢弃一些趋势相关性弱的特征了，看看预测效果是否有提高。

我们可以看到，丢弃特征的相关性阈值越高，排行榜（LB）上的AUC越高。只要注意不要丢弃重要特征，AUC可以提升到0.74。有趣的是，测试集的AUC并没有像排行榜的AUC变化那么大。完整代码可以在featexp_demo记事本里面找到。

featexp_demo

https://github.com/abhayspawar/featexp/blob/master/featexp_demo.ipynb

特征工程

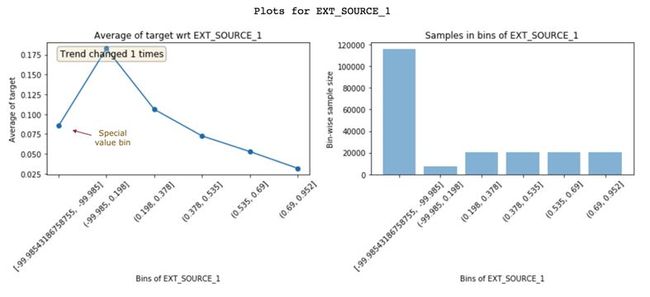
通过查看这些图表获得的见解，有助于我们创建更好的特征。只需更好地了解数据，就可以实现更好的特征工程。除此之外，它还可以帮助你改良现有特征。下面来看另一个特征EXT_SOURCE_1：

                     

具有较高EXT_SOURCE_1值的客户违约率较低。但是，第一个区间（违约率约8％）不遵循这个特征趋势（上升并下降）。它只有-99.985左右的负值且人群数量较多。这可能意味着这些是特殊值，因此不遵循特征趋势。幸运的是，非线性模型在学习这种关系时不会有问题。但是，对于像Logistic回归这样的线性模型，如果需要对特殊值和控制进行插值，就需要考虑特征分布，而不是简单地使用特征的均值进行插补。

特征重要性

Featexp还可以帮助衡量特征的重要性。DAYS_BIRTH和EXT_SOURCE_1都有很好的趋势。但是，EXT_SOURCE_1的人群集中在特殊值区间中，这表明它可能不如DAYS_BIRTH那么重要。基于XGBoost模型来衡量特征重要性，发现DAYS_BIRTH实际上比EXT_SOURCE_1更重要。

特征调试

查看Featexp的图表，可以帮助你通过以下两项操作来发现复杂特征工程代码中的错误：

                

零方差特征只展现一个区间

• 检查要素的总体分布是否正确。由于一些小错误，我个人曾多次遇到类似上述的极端情况。
• 在查看这些图之前，预先假设特征趋势可能会是怎样，特性趋势如果不像你所期望的那样，这可能暗示了一些问题。坦白地说，这个假设趋势的过程使构建机器学习模型变得更加有趣!

泄漏检测

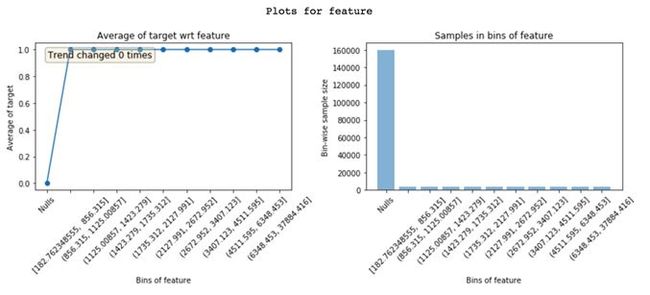
从目标到特征的数据泄漏会导致过拟合。泄露的特征具有很高的特征重要性。要理解为什么在特征中会发生泄漏是很困难的，查看featexp图像可以帮助理解这一问题。

在“Nulls”区间的特征违约率为0％，同时，在其他所有区间中的违约率为100％。显然，这是泄漏的极端情况。只有当客户违约时，此特征才有价值。基于此特征，可能是因为一个故障，或者因为这个特征在违约者中很常见。了解泄漏特征的问题所在能让你更快地进行调试。

                              

理解为什么特征会泄漏

模型监控

由于featexp可计算两个数据集之间的趋势相关性，因此它可以很容易地利用于模型监控。每次我们重新训练模型时，都可以将新的训练数据与测试好的训练数据（通常是第一次构建模型时的训练数据）进行比较。趋势相关性可以帮助你监控特征信息与目标的关系是否发生了变化。

 

这些简单的步骤总能帮助在Kaggle或者实际工作中构建更好的模型。用featexp，花15分钟去观察那些图像，是十分有价值的：它会带你一步步看清黑箱里的世界。

 

建模后的特征重要性（模型可解释性）

深度神经网络能够在多个层次进行抽象推断，所以他们可以处理因变量与自变量之间非常复杂的关系，并且达到非常高的精度。但是这种复杂性也使模型成为黑箱，我们无法获知所有产生模型预测结果的这些特征之间的关系，所以我们只能用准确率、错误率这样的评价标准来代替，来评估模型的可信性。

但我们在构建树类模型（XGBoost、LightGBM等）时，想要知道哪些变量比较重要的话。可以通过模型feature_importances_方法来获取特征重要性。例如LightGBM的feature_importances_可以通过特征的分裂次数或利用该特征分裂后的增益来衡量。

对模型结果的解释可应用到以下这些场景当中：

数据收集

对于从网上下载的数据集，你是无法控制的。但是很多使用数据科学的企业和组织都有机会扩展所收集数据的类型。因为收集新类型的数据可能成本会很高，或者非常麻烦，所以只有在清楚这么做是划算的时候，企业和组织才会去做。基于模型的解释会帮你更好地理解现有特征地价值，进而推断出哪些新数据可能是最有帮助的。

决策制定

某些情况下，模型会直接自动做出决策，但是有很多重要的决策是需要人来确定。对于最终需要人来做的决策，模型的可解释性比单纯的预测结果更重要。

建立信任

许多人在确定一些基本的事实之前，不会信赖你用来做重要决策的模型。鉴于数据错误的频繁出现，这是一种明智的防范措施。在实际业务场景中，如果给出的模型解释符合对方自身对问题的理解，那么即使在基本不具备深入的数据科学知识的人之间，也将有助于建立互相信任的关系。

1.Permutaion Importance —— 排列重要性

训练得到一个模型之后，我们可能会问的一个最基本的问题是 哪些特征对预测结果的影响最大？

这一概念叫做 特征重要性。

我们想用一个人10岁的数据去预测他20岁的身高是多少？

数据中包含：

• 有用的特征（10岁时的身高）
• 较弱的特征（10岁时每天体育锻炼的时间）
• 对预测基本没有作用的特征（10岁时股票数量）

排列重要性是要在模型拟合之后才能进行计算。 所以对于给定的身高、股票数量等取值之后，计算排列重要性并不会改变模型或者是它的预测结果。

相反，我们会问以下问题：如果随机打乱验证数据某一列的值，保持目标列以及其它列的数据不变，那么这种操作会在这些打乱的数据上对预测准确率产生怎样的影响？

对某一列进行随机排序应当会降低预测的准确率，这是因为产生的数据不再对应于现实世界中的任何东西。如果随机打乱的那一列模型预测对其依赖程度很高，那么模型准确率的衰减程度就会更大。在这个例子中，打乱height at age 10将会让预测结果非常差。但是如果我们随机打乱的是socks owned，那么产生的预测结果就不会衰减得那么厉害。

有了上述认识之后，排列重要性就按照以下步骤进行计算：

1. 得到一个训练好的模型
2. 打乱某一列数据的值，然后在得到的数据集上进行预测。用预测值和真实的目标值计算损失函数因为随机排序升高了多少。模型性能的衰减量代表了打乱顺序的那一列的重要程度。
3. 将打乱的那一列复原，在下一列数据上重复第2步操作，直到计算出了每一列的重要性。

                                                               

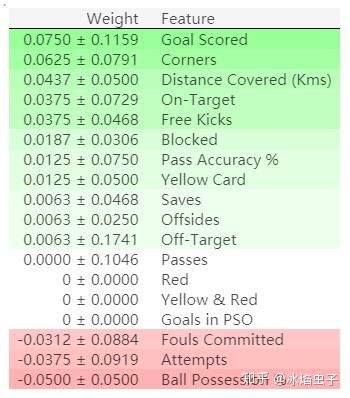
排列重要性结果解读

排在最上面的是最重要的特征，排在最下面是重要性最低的特征。

每一行的第一个数字表示模型性能衰减了多少（在这个例子中，使用准确率作为性能度量）。

跟数据科学里面的很多事情一样，在对某一打乱的特征提取重要性的时候，是存在随机性的，所以我们在计算排列重要性的时候，会通过多次打乱顺序的方式重复这一过程。在±后面的数字表示标准差。

偶尔你会看到负值的排列重要性。在这些情况中，在打乱的数据上得到预测结果比真实数据的准确率更高。这在所选特征与目标基本无关（重要性应该为0）的情况下会出现，但是随机的因素导致预测结果在打乱的数据上表现得更准确。就像这个例子一样，因为没有容忍随机性的空间，这种情况在小的数据集上很常见。

2.Partial Dependence Plots —— 部分依赖图

特征重要性展示的是哪些变量对预测的影响最大，而部分依赖图展示的是特征如何影响模型预测的。

部分依赖图可以用来展示一个特征是怎样影响模型预测的。可以用部分依赖图回答一些与下面这些类似的问题：1. 假如保持其它所有的特征不变，经纬度对房价有什么影响？换句话说，相同大小的房子，在不同的地方价格会有什么差别？2. 在两组不同的人群上，模型预测出的健康水平差异是由他们的负债水平引起的，还是另有原因？

工作原理

跟排列重要性一样，部分依赖图也是要在拟合出模型之后才能进行计算。 模型是在真实的未加修改的真实数据上进行拟合的。

以足球比赛为例，球队间可能在很多方面都存在着不同。比如传球次数，射门次数，得分数等等。乍看上去，似乎很难梳理出这些特征产生的影响。

为了搞清楚部分依赖图是怎样把每个特征的影响分离出来的，首先我们只看一行数据。比如，这行数据显示的可能是一支占有50%的控球时间，传了100次球，射门了10次，得了1分的球队。

接下来，利用训练好的模型和上面的这一行数据去预测该队斩获最佳球员的概率。但是，我们会多次改变某一特征的数值，从而产生一系列预测结果。比如我们会在把控球时间设成40%的时候，得到一个预测结果，设成50%的时候，得到一个预测结果，设成60%的时候，也得到一个结果，以此类推。以从小到大设定的控球时间为横坐标，以相应的预测输出为纵坐标，我们可以把实验的结果画出来。

from matplotlib import pyplot as plt
from pdpbox import pdp, get_dataset, info_plots

# Create the data that we will plot
pdp_goals = pdp.pdp_isolate(model=tree_model, dataset=val_X, model_features=feature_names, feature='Goal Scored')

# plot it
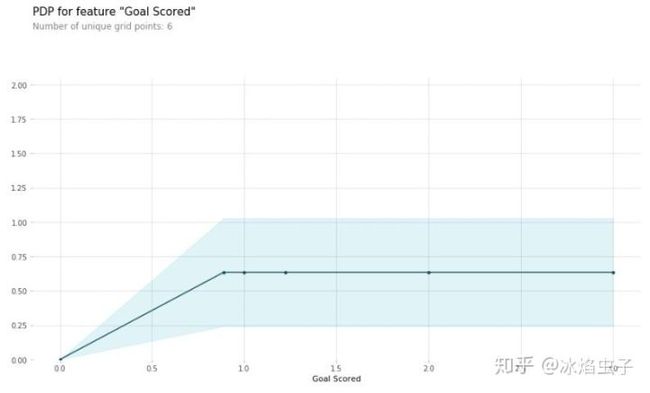
pdp.pdp_plot(pdp_goals, 'Goal Scored')
plt.show()

                                                                     

在看上面的部分依赖图的时候，有两点值得注意的地方：

• y轴表示的是模型预测相较于基线值或最左边的值的变化。
• 蓝色阴影部分表示置信区间。

2D 部分依赖图

如果你对特征之间的相互作用感兴趣的话，2D部分依赖图就能排得上用场了。

key code:
from sklearn.ensemble.partial_dependence import partial_dependence, plot_partial_dependence

my_plots = plot_partial_dependence(my_model,       
                                   features=[0, 2], # column numbers of plots we want to show
                                   X=X,            # raw predictors data.
                                   feature_names=['Distance', 'Landsize', 'BuildingArea'], # labels on graphs
                                   grid_resolution=10) # number of values to plot on x axis

优点

pdp的计算是直观的：partial dependence function 在某个特定特征值位置表示预测的平均值，如果我们强制所有的数据点都取那个特征值。在我的经验中，lay people(普通人，没有专业知识的大众)通常都可以很快理解PDPs的idea。

如果你要计算的PDP的特征和其它特征没有关联，那么PDP可以完美的展示出这个特征大体上上如何影响预测值的。在不相关的情况下，解释是清晰的：PDP展示了平均预测值在某个特征改变时是如何变化的。如果特征是相互关联的，这会变得更加复杂。

不足

实际分析PDP时的最大特征个数是2。这不是PDP的错误，而是由于我们人无法想象超过三维的空间。

有一些 PDP并不展示特征分布。忽略分布可能会造成误解，因为你可能会过度解读具有少量数据的地方。这个问题通过展示一个rug或者histogram在x轴上的方式很容易解决。

独立性假设是PDP的最大问题，它假设计算的特征和其它特征是不相关的。当特征是相关的时候，我们创造的新的数据点在特征分布的空间中出现的概率是很低的。对这个问题的一个解决方法就是Accumulate Local Effect plots，或者简称ALE plots，它工作在条件分布下而不是边缘分布下。

多种类的影响可能会被隐藏，因为PDP仅仅展示边际影响的平均值。假设对于一个要计算的特征，一半的数据点对预测有正相关性，一半的数据点对预测有负相关性。PD曲线可能会是一个水平的直线，因为两半数据点的影响可能会互相抵消。然后你可能会得出特征对预测没有影响的结论。通过绘制individual conditional expectation curves而不是aggregated line，我们可以揭示出这种heterogeneous effects。

3.SHAP VALUES —— 什么影响了你的决定？

 

SHAP值（SHapley Additive exPlanations的缩写）从预测中把每一个特征的影响分解出来。可以把它应用到类似于下面的场景当中:

• 模型认为银行不应该给某人放贷，但是法律上需要银行给出每一笔拒绝放贷的原因。
• 医务人员想要确定对不同的病人而言，分别是哪些因素导致他们有患某种疾病的风险，这样就可以因人而异地采取针对性的卫生干预措施，直接处理这些风险因素。

工作原理

SHAP值通过与某一特征取基线值时的预测做对比，来解释该特征取某一特定值的影响。

可以继续用排列重要性和部分依赖图中用到的例子进行解释。

我们对一个球队会不会赢得“最佳球员”称号进行了预测。

我们可能会有以下疑问：

• 预测的结果有多大的程度是由球队进了3个球这一事实影响的？

但是，如果我们像下面这样重新表述一下的话，那么给出具体、定量的答案还是比较容易的：

• 预测的结果有多大的程度是由球队进了3个球这一事实影响的，而不是某些基线进球数？

当然，每个球队都由很多特征，所以，如果我们能回答“进球数”的问题，那么我们也能对其它特征重复这一过程。

import shap  

#实例化
explainer = shap.TreeExplainer(my_model)

#计算
shap_values = explainer.shap_values(data_for_prediction)

shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)

 

我们预测的结果时0.7，而基准值是0.4979。引起预测增加的特征值是粉色的，它们的长度表示特征影响的程度。引起预测降低的特征值是蓝色的。最大的影响源自Goal Scored等于2的时候。但ball possesion的值则对降低预测的值具有比较有意义的影响。

如果把粉色条状图的长度与蓝色条状图的长度相减，差值就等于基准值到预测值之间的距离。

要保证基线值加上每个特征各自影响的和等于预测值的话，在技术上还是有一些复杂度的（这并不像听上去那么直接）。我们不会研究这些细节，因为对于使用这项技术来说，这并不是很关键。这篇博客对此做了比较长篇幅的技术解释。

如果仔细观察一下计算SHAP值的代码，就会发现在shap.TreeExplainer(my_model)中涉及到了树。但是SHAP库有用于各种模型的解释器。

• shap.DeepExplainer适用于深度学习模型
• shap.KernelExplainer 适用于各种模型，但是比其它解释器慢，它给出的是SHAP值的近似值而不是精确值。
  下面是用KernelExplainer得到类似结果的例子。结果跟上面并不一致，这是因为KernelExplainer`计算的是近似值，但是表达的意思是一样的。

4.Summary Plots

explainer = shap.TreeExplainer(my_model)

shap_values = explainer.shap_values(val_X)

shap.summary_plot(shap_values[1], val_X)

                                            

图形解释

• 每个点是一个样本（人），图片中包含所有样本

• X轴：样本按Shap值排序-

• Y轴：特征按Shap值排序

• 颜色：特征的数值越大，越红

特征解释：

• martial_status2这个特征最重要，且值越大，收入会相对更高，到达一定峰值，会明显下降

• 年龄也是影响结果的重要特征，年龄小收入普遍低，但年龄到达一定程度，并不会增加收入，存在年龄小，收入高的人群。

• 收入水平和capital_gain大致呈正相关。

shap.summary_plot(shap_values[1],X_test, plot_type="bar")

                                                

上图是特征重要性图谱，由上向下重要性依次减弱。

shap_values = explainer.shap_values(df)
shap.dependence_plot('age', shap_values[1], df, interaction_index="capital_gain")

 

                                              

图形解释:

• X轴：age

• Y轴（左）：一个样本的age对应的Shap值

• 颜色：capital_gain越大越红

特征解释:

• 排除所有特征的影响，描述age和capital_gain的关系。

• 年龄大的人更趋向于有大的资本收益，小部分年轻人有大的资本收益。

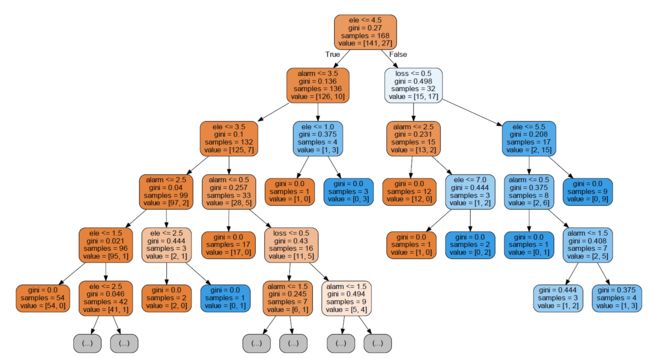
5.树GraphViz可视化export_graphviz

export_graphviz(estimator, out_file='tree.dot', 
                feature_names = feature_names,
                class_names = y_train_str,
                rounded = True, proportion = True, 
                label='root',
                precision = 2, filled = True)

from subprocess import call
call(['dot', '-Tpng', 'tree.dot', '-o', 'tree.png', '-Gdpi=600'])

from IPython.display import Image
Image(filename = 'tree.png')

 

写到这里就告一段落。

后来发现了一个更全面的学习博文，更进一步参考。

https://blog.csdn.net/Datawhale/article/details/103169719