Nature:相同fMRI数据集多中心分析的变异性
一、引言
许多科学领域的数据分析工作已经变得越来越复杂和灵活,这也意味着即使相同的数据,不同研究者采用的处理方法和步骤也可能不同,那么得到的结果也不尽然一致。近期,Nature杂志发表一篇题目为《Variability in the analysis of a single neuroimaging dataset by many teams》的研究论文,该研究通过要求70个独立团队分析相同的fMRI数据集,测试相同的9个预先假设,来评估功能磁共振成像(fMRI)结果的这种灵活性的效果。分析方法的灵活性体现在没有两个团队选择相同的方式来分析数据。这种不确定性导致了假设检验结果的巨大差异。报告结果的差异与分析方法的多个方面有关。研究人员的预测市场显示,即使是了解数据集的研究人员,也过高估计了重要发现的可能性。该研究结果表明,分析的灵活性可以对科学结论产生重大影响,并在fMRI分析中识别出可能与变异性有关的因素。该研究的结果强调了验证和共享复杂分析工作的重要性,并说明了对相同数据执行和报告多重分析的必要性。此外,该研究还讨论了可用于减轻与分析变异性有关的问题的潜在方法。
二、背景
科学领域的数据分析工都有着大量的分析步骤,这些步骤涉及许多可能的选择。模拟研究表明,分析选择的不同可能对结果产生重大影响,但其程度及其在实践中的影响尚不清楚。最近的一些心理学研究通过使用多个分析人员的方法解决了这一问题。在这种方法中,大量的小组分析同一数据集,研究发现分析小组的行为结果有很大的差异。在神经影像学分析复制和预测研究(NARPS)中,该研究将类似的方法应用于分析工作流程复杂且变化多样fMRI领域。研究者的目标是以最高的生态效度来评估分析灵活性对fMRI结果的实际影响程度。此外,研究者们使用预测市场(Prediction markets)来测试该领域的同行是否能够预测结果以及估计该领域研究人员对分析结果变异性程度的信念。
三、结果
1.跨团队的结果变异性
NARPS的第一个目标是评估分析相同数据集的独立团队的结果在现实中的变异性。该数据集包括来自108个被试的fMRI数据,每个被试执行一个任务两个版本中的一个,该任务之前被用于研究风险决策。这两个版本的设计是为了解决在任务中关于增益和损耗分布对神经活动影响的争论(数据信息见原文辅助材料)。。
在向70个团队(其中69个团队以前发表过fMRI)提供了原始数据和可选的数据集预处理版本(使用fMRIPrep)后,他们被要求对数据进行分析,以测试9个事先假设(表1),每个假设都包含了与任务特定特征相关的特定脑区活动的描述。分析时间为100天的,各小组需要在全脑校正分析(Whole-brain-corrected analysis)的基础上,报告每个假设是否得到了支持(是或否)。此外,每个小组提交了一份详细的分析方法报告,以及支持每个假设检验的无阈值和有阈值统计图(表2,3a)。为了进行生态效度研究,给这些分析团队唯一的指令就是像往常在自己的实验室里一样进行分析工作,并根据他们自己的标准报告二元决策,即假设中描述的特定区域的全脑校正结果。在预测市场关闭之前,数据集、报告和集合都是保密的。
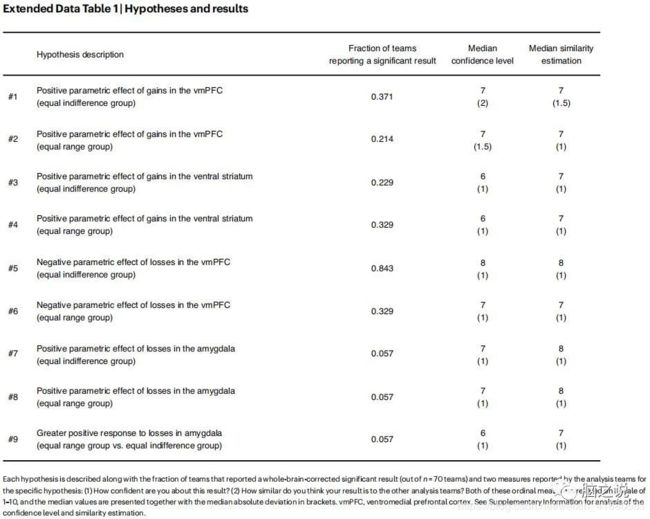 表1
表1
表2
表3
总体而言,不同假设之间报告的显著性结果的比率不同 (图1,表1)。只有一个假设(假设5)的显著性结果的比率较高(84.3%),而其他三个假设的在团队间有着一致非显著性结果(只有5.7%报告为显著性结果)。而剩下的5个假设结果比率是各不相同的,从21.4%到37.1%的团队报告了一个显著的结果。不同团队之间结果的差异程度是由报告结果与大多数团队不同的团队所占的比例来衡量的。平均来说,20%团队报告的结果与大多数团队不同。假设最大可能的偏差为50%,那么20%差异结果的观察分数介于团队之间的完全一致性和完全随机之间,这表明分析的选择对报告结果有着重要影响。
2.与分析变异性有关的因素
为了检验报告的二元结果中分析变异性的来源,研究者们分析了团队使用的Pipeline以及他们提供的无阈值和阈值统计图。没有两个团队拥有相同的Pipeline。排除一些团队(表3b)后,65个团队的阈值映射和64个团队的无阈值映射(z-或t-统计)被纳入分析。
3.报告结果的变异性
一组混合效应逻辑回归模型(mixed-effectslogistic regression models)确定了与报告结果相关的几个分析变量和图像特征(表3c)。其中最显著的影响因素是空间平滑度;无阈值统计图较高的估计平滑度(使用FSL的估计平滑度函数)与更大显著性结果的可能性相关(P <0.001,delta pseudo-R2= 0.04;在半最大值处的平均全宽9.69mm,跨队距离2.50- 21.28mm)。值得注意的是,尽管估计的平滑度与应用的平滑核的宽度有关(r = 0.71;中位数应用平滑5mm,团队间0-9mm)但在单独的分析中,应用平滑值本身与阳性结果没有显著的相关,这表明相关自于分析步骤,而不是平滑(例如头部运动的建模;P= 0.014)。使用的软件包对结果也有影响(P= 0.004, delta pseudo-R2=0.04; n = 23 (SPM), n = 21 (FSL), n = 7 (AFNI)和n = 13(其他软件包),与SPM相比,FSL与所有假设显著结果的可能性更高;让步比=6.69),另外不同的多重校正方法对结果也有影响(P= 0.024, deltapseudo-R2= 0.02: n = 48(参数),n = 14(非参数),n = 2(其他)),采用参数校正方法的检测率高于非参数方法。使用标准化步骤预处理数据与使用自定义预处理pipeline,或使用用头部运动参数建模相比,未发现显著影响。非参数bootstrap分析证实了空间平滑度的显著影响,但对多重测试和软件包的影响提供了不一致的支持;由于统计能力较低,这些结果应谨慎解释。
4.阈值统计图的变异性
通过分析研究小组提交的统计图,进一步探讨分析变异性的性质。阈值映射是高度稀疏的。所有体素的阈值映射之间的二元一致性较高(假设的中位数百分比一致性在93%到99%之间),这主要反映了那些体素不活跃的一致性。然而,在所有团队中都激活的体素重叠非常低(假设的中位数相似性从0.00到0.06)。这可能反映了每个团队发现的激活体素数量的变异性;对于每个假设,活跃体素的数量在团队中从0到数万个之间变化(表4a)。对激活体素重叠的分析表明,在给定的假设条件下,最频繁激活的体素中激活的团队比例在0.23到0.77之间(附图1)。

表4
附图1
5.无阈值统计图的变异性
对团队间无阈值z统计图的相关性分析表明,对于每个假设,拥有大的cluster的研究团队之间具有着很强正相关(图2,附图2)。所有无阈值映射对(表4b)之间的平均Spearman相关是中等的(假设间的平均相关性范围为0.18-0.52),在分析团队的主聚类中相关性更高(假设间的相关性范围为0.44 -0.85)。对无阈值映射(相当于tau-squared)的体素异构性进行的分析表明,在许多情况下,团队之间的差异很大,是不同数据集的预期差异的几倍(附图3a)。
图2
附图2
附图3
对于假设1和假设3,有7个团队的一个子集,其无阈值映射与主大多数团队的映射不相关。通过对假设1和假设3的反向相关聚类的平均map图进行比较,可以证实该map图与总体任务激活map高度相关(r= 0.87)。进一步的分析表明,有4个团队使用的模型没有恰当地将增益的参数效应与整体任务激活分开;由于价值系统激活与任务激活之间存在对抗关系,该模型的模型误定导致了具有增益参数效应的对抗关系。
无阈限映射的总体相关与报告的二元结果之间的分歧(即使在高度相关的集群)表明,局部结果的差异可能是由于与多重比较校正有关的程序和团队对感兴趣区域(ROIs)的主观决定造成的。为了测试这一点,研究者在每个假设的所有团队的无阈值映射上应用了一致的阈值方法和ROI的解剖定义。结果表明,即使使用已知的自由的修正方法和标准的区域解剖定义,不同结果的差异程度在质量上依旧与实际报告的相似(附图4)。

附图4
该研究使用基于图像的元分析来评估团队间的一致性,在FDR校正后(附图3b),除了假设9之外,所有假设都显示出显著性的激活体素(active voxels),并为假设2、4、5和6提供了验证性证据。这些结果表明,在单个团队上的不一致结果构成了团队结果合并时的一致性结果的基础。
6.预测市场
NARPS的第二个目标是测试该领域的同行是否能够预测结果,方法就是是利用预测市场这一在风险决策中的常用方法。在这个市场中,研究人员根据科学分析的结果进行交易,并根据业绩获得奖金。预测市场已经被用来评估社会科学中科学假设的可复制性,并揭示了市场价格和实际科学结果之间的相关性。该进行了两个独立的预测市场:一个是来自分析团队成员组成的市场(团队成员市场),另一个是没有参与分析的研究人员组成的独立市场(非团队成员市场)。在所有分析小组提交了他们的结果(这些结果是保密的)之后,市场连续开放10天,持续时间1.5个月。在每个市场,交易员都会得到价值50美元的代币,并通过在线市场平台进行交易,交易对象是报告每个假设(即基本值)显著性结果的团队的比例。市场价格是交易员总体信念的衡量指标,反映的是对每个假设报告显著性结果的团队所占比例。总体而言,n= 65名交易员在非团队成员市场交易活跃,n= 83名交易员在团队成员市场交易活跃。在股市收盘后,交易员的报酬根据他们在市场的表现而定的。市场分析是在开放科学框架(OSF)上预先注册的(https://osf.io/59ksz/)。请注意,由于对最终市场价格(即市场的预测)进行了一些分析,每个市场的每个假设都有一个值,因此每个市场的观察次数都很低(n= 9),导致统计能力有限。因此,对结果的解释应当谨慎。
团队成员市场的预测范围从0.073到0.952 (M= 0.599, SD =0.325),非团队成员市场的预测范围从0.476到0.882 (M= 0.690, SD = 0.137)。除团队成员市场假设7外,所有预测均在基本值的95%置信区间之外(图1,表5a)。基本价值和市场预测之间的斯皮尔曼相关性在团队成员市场中显著(r = 0.962, P <0.001, n = 9),但非团队成员市场(r = 0.553, P = 0.122, n = 9)及两个市场的预测之间都不显著(r = 0.500, P = 0.170, n = 9)。
表5
Wilcoxon signed-rank检验表明,两个市场的交易员系统地高估了基本价值(团队成员:z= 2.886, P = 0.004, n = 9;非团队成员:z= 2.660, P = 0.008, n = 9)。团队成员市场的结果不是由报告显著结果(补充方法和补充结果)的团队的比例过高所驱动的。团队成员市场的预测与非团队成员市场的预测没有显著差异(Wilcoxon signed-rank检验,z = 1.035, P = 0.301, n = 9),但如上所述,该检验的统计能力有限。团队成员通常按照与自己团队的结果一致的方向交易(表5 b),这可能解释了为什么他们的集体预测比非团队成员的预测更准确(图1)。其他研究的结果发表在补充信息(附图5,表5)。
附图5
四、讨论
70个独立的分析团队分析了一个fMRI数据集,他们都使用了不同的pipeline,结果显示报告的二元结果有很大的差异,团队之间对大多数测试假设的分歧很大。对于每个假设,至少可以找到四种不同的分析方法,这些方法被该领域的研究小组在实践中使用,并产生了显著的结果。该研究结果强调了这样一个事实,即很难估计使用单一pipeline进行的单一研究的复现性。值得注意的是,对假设检验所依据的基础统计参数图的分析显示,其一致性比从这些推断得出的结果更大,并且使用元分析观察到了各团队激活区域的显著一致性。具有高度相关的基础无阈值统计图的团队报告了不同的假设结果(图2)。分析小组提交的工作流程描述和统计结果的详细分析确定了几个与重要结果的差异报告相关的常见分析变量,包括数据的空间平滑、分析软件的选择和校正方法;然而,后两种方法并没有得到非参数分析的一致支持。此外,研究者们确定了几个分析团队模型误定,这导致统计图与一些假设的多数相关。对分析结果进行的预测市场显示,研究人员普遍高估了各种假设得出重要结果的可能性,甚至是那些分析了数据的研究人员本身也反映出该领域研究人员明显的乐观偏见。
大量的分析可变性以及报告的假设结果在相同数据下的后续可变性表明,需要采取措施来提高数据分析结果的可重复性。首先,该研究建议使用诸如NeuroVault15之类的工具,将无阈值统计图与有阈值统计图作为标准共享。从长远来看,共享地图将允许使用基于图像的元分析,该发现它可以在实验室之间提供聚合结果。其次,数据和分析代码的共享应该成为一种常见的实践,以使其他人能够使用相同的数据运行自己的分析或验证所使用的代码。这些做法,再加上使用预先登记或注册的报告,将减少研究人员的自由度,但不会防止分析的变异性;然而,他们将确保变异性的影响是可以评估的。该研究中使用的所有数据和代码都是公开的,并且对于所有数据和结果都有一个完全可复制的执行环境。研究者们认为这可以作为今后研究的一个范例。
首先,研究者们建议使用多个pipeline分析复杂的数据集,最好由多个研究团队进行分析。要实现这种大规模的“多元宇宙分析(Multiverse analysis)”,需要开发自动化的统计分析工具(例如,FitLins18),它可以运行广泛的pipeline,并评估它们的收敛性。这种“多元宇宙分析”的不同版本已经在其他领域提出,但尚未得到广泛应用。另外,还应该使用模拟数据验证pipeline,以评估其有效性,并评估其对新数据的预测的影响。
该研究的结果强调开发新的实践和工具的迫切需要,以克服跨pipeline的变异性的挑战及其对分析结果的影响。尽管如此,研究者们认为fMRI可以为科学问题提供可靠的答案,这在跨团队的元分析结果中得到了强有力的证明。同时文献中也有大量的大规模研究和使用fMRI复制了许多发现。此外,虽然目前的研究仅限于分析单一的fMRI数据集,但似乎很有可能在其他研究领域也存在类似的变异性。在这些领域中,数据是高维的,分析工作流程是复杂和多变的。多元宇宙方法结合元分析被认为是解决这个问题的一个有希望的解决方案。
注:原文文献资料请加赵老师微信索要(kervin_zhao)
