《大话数据结构》阅读笔记。第四天。2018-7-26（KMP算法）

继续KMP算法。

for (int q = 1; q <= len-1; q++)
{
   while (k > -1 && str[k + 1] != str[q])
         {
             k = next[k];
         }
   if (str[k + 1] == str[q])
        {
             k = k+1;
         }
    next[q] = k;
}

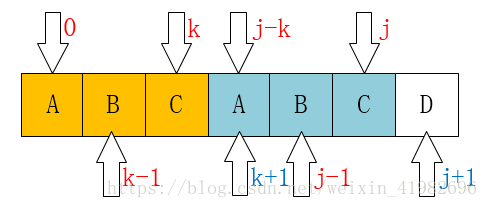
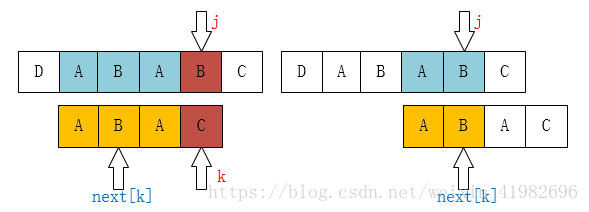
理解代码，最重要的是这两张图象：

当p[k]=p[j]时，

那么next[j+1]=next[j]+1=k+1.

如果p[k] !=p[j]，

那 k=next[k]；

怎么理解。首先我觉得q就是j。假设现在要计算next[j]的k。j-1已经计算过了得到了j-1的next值k1（k1即是个长度即next[]的值，那这个next[]代表什么意思，那就是当j这个位置不匹配时下一个要移动到的位置是k1，以前是从头在比较，现在是从k1的位置比较，所以k1还是个位置）。那怎么算j处的k？用k1+1，怎么用？看k1+1处的字符和j处的字符是否相等，也就是p[k1+1]=？p[j]。为什么要用k1+1的字符计算？因为计算j-1的k1时已经计算了j-1处的最大长度k1，当要计算j处的k的时候，k最多也就比k1大1个，而这大的一个只可能是k1+1处的字符。当k1+1处的字符和j处的字符一样的时候（if里面的），那长度值就可以加1；否则不一样的话最大长度就是k（while里面的）。

看代码部分：

最终是要求q从1到len-1的所有位置的next[q]的k。

例如：  记着要比较

str[k + 1] == str[q]

位置：1   2   3   4   4   5   6   7   8   9

字符：0   a   b   a   b   a   a   a   b   a

K值：-1  -1  -1  0   1   2   0   0   1   2      （k=-1说明长度为0，0长度为1，1长度为2，2长度为3）

第一个位置0：netx[0]=-1=k ( k初始化-1 )。

第二个位置a：next[q]=next[1]=k=-1。

第三个位置b：next[q]=next[2]，k+1=-1+1=0，str[0]==str[2]？a!=b，进入while语句，k=-1。

第四个位置a：next[q]=next[3]，k+1=-1+1=1，str[1]==str[3]？b==b，进入if语句，k=k+1=1.

第五个位置a：next[q]=next[4]，k+1=1+1=2，str[2]==str[4]？a==a，进入if，k=2，

第六个位置a：next[q]=next[5]，k+1=2+1=3，str[3]==str[5]？b!=a，进入while语句，k=next[k]=next[2]=0。

第七个位置a：next[q]=next[6]，k+1=0+1=1，str[1]==str[6]？b!=a，进入while语句，k=next[k]=next[0]=0。

第八个位置b：next[q]=next[7]，k+1=0+1=1，str[1]==str[7]？b==b，进入if，k=1。

第九个位置a：next[q]=next[8]，k+1=1+1=2，str[2]==str[8]？a==a，进入if，k=2。

 

看不懂没关系，因为我胡写的（本来是认真写，越写感觉越不会），操各种版本的都有，有从0开始的，有从1开始的，有叫k的叫q的，同一个ababaaaba有各种版本的next值，对next的定义都不一样。有的有10个值有的有9个值，越看越糊涂，本来以为自己理论懂了只是代码没懂，现在tmd理论感觉都有问题。下面再尝试写一个版本的，能不能写完现在不知道，直接翻到最下面看我有没有写成功，写成功了在看，没成功怎么办心里有点X数吧。

 

 

这下参考https://cloud.tencent.com/info/6420aa15efcb27ad41296edbefd345a5.html 这个X 的。

这里有个概念和上面一样，长度。比如abc，长度就是0，aba，长度就是1，abab长度就是2。这要是不知道回家给7酱养猪吧，看上面的理论。

直接上例子：

位置：1   2   3   4 

字符：a   b   c   d

       ：0   1   1   1

先不看代码，看理论怎么得next[j]的值，别叫k了，就叫next[]。理论：

next[a]=next[1]=0；    人为规定的，你看谁第一个不是0或者-1.  

next[b]=next[2]=1；   b前面只有a，长度是0，“”那就等于1.

next[c]=next[3]=1；    c前面只有ab，长度是0， “”那就等于1.

next[d]=next[4]=1；   d前面只有abc，长度是0，  “”那就等于1.

 

位置：1   2   3   4   5   6   7   8   9     也就是j，没有其他字母，就叫j

字符：a   b   a   b   a   a   a   b   a

       ：0   1  1   2   3   4   2   2   3

理论：

next[a]=next[1]=0；  

next[b]=next[2]=1；  b前面只有a，长度是0，""  那就等于1。

next[a]=next[3]=1;    a前面只有ab，长度是0，""  那就等于1。

next[b]=next[4]=2;    b的前面是aba，长度是1，"a"  那就等于2.

next[a]=next[5]=3;    a的前面是abab，长度是2，"ab"  那就等于3.

next[a]=next[6]=4;    a的前面是ababa，长度是3，"aba"  那就等于4.

next[a]=next[7]=2;    a的前面是ababaa，长度是1，"a"  那就等于2.

next[b]=next[8]=2；  b的前面是ababaaa，长度是1，"a"  那就等于2.

next[a]=next[9]=3；  a的前面是ababaaab，长度是2，"ab"  那就等于3.

至于ababaaaba的长度，不用管这个，都全部了已经匹配了。

之所以用这个是因为和书上的结果一样。不存在什么相等不相等。

理论就这样，看代码部分：

void get_next(char *T,int *next)
{
     int i,j;
      i=1;
      j=0;
      next[1]=0;
    while ( i

先看第一个例子“abcd”，一开始i=1，j=0，，进入if，i=2，j=1，next[2]=1。第二轮，T[i]=T[2]=b!=T[j]=T[1]=a，进入else，j=next[j]=next[1]=0。第三轮，j=0，进入if，i=3，j=1，next[3]=1。第四轮，j=next[j]=0。省略。next[4]=1。

在看第二个例子“ababaaaba”，

初始化：################################################next[1]=0

一开始：i=1，j=0，进入if。i=2，j=1，next[2]=1。#################next[2]=1

第二轮：i=2，j=1，T[i]=b!=T[j]=a，进入else。j=next[1]=0。

第三轮：i=2，j=0，进入if。i=3,j=1，next[3]=1。##################next[3]=1

第四轮：i=3，j=1，T[i]=a==T[j]=a，进入if。i=4，j=2，next[4]=2######next[4]=2

第五轮：i=4，j=2，T[i]=b==T[j]=b，进入if。i=5，j=3，next[5]=3######next[5]=3

第六轮：i=5，j=3，T[i]=a==T[j]=a，进入if。i=6，j=4，next[6]=4######next[6]=4

第七轮：i=6，j=4，T[i]=a!=T[j]=b，进入else。j=next[4]=2

第八轮：i=6，j=2，T[i]=a!=T[j]=b，进入else。j=next[2]=1

第九轮：i=6，j=1，T[i]=a==T[j]=a，进入if。i=7，j=2，next[7]=2######next[7]=2

第十轮：i=7，j=2，T[i]=a!=T[j]=b，进入else。j=next[2]=1

第十一轮：i=7，j=1，T[i]=a==T[j]=a，进入if。i=8，j=2，next[8]=2#####next[8]=2

第十二轮：i=8，j=2，T[i]=b==T[j]=b，进入if。i=9，j=3，next[9]=3#####next[9]=3

马币的终于写完了，但是的得到这些next值怎么用呢，接下来就是KMP：

int Index_KMP(char* S,char* T,int pos)        //T是子串
{
   int i=pos;
   int j=1                        //i为主串中的位置，j为子串中的位置
   int next[255];
   get_next(T, next);
   
   while(i<=strlen(S)&&j<=strlen(T))
      {
          if(j==0||S[i]==T[j])    //字符相等
              {
                     i++;
                     j++;
              }
           else 
                    j=next[j];      //j回到next的位置，i不变
      }
    if(j>strlen(T))
          return (i-strlen(T)-1);
    else
          return  0;
}

时间复杂度为O(n+m)。

整个例子：

int main()

{

　　char* T="bc";

　　 char* S="babaacbababcbababcbcbc";

　　 int pos=1;

　　int next[255];

　　get_next(T,next);

　　for(int j=1;j<=2;j++)

　　 cout<<"j="<

具体怎么用的，当不相等的时候 j=next[j]，其实需要先看看朴素的笨办法，在看这个才能彻底明白怎么用的。不过next的值是知道了。可以看上面的。

今天的任务还没开始，都6点半了，一天就看了看KMP算法还没彻底搞懂，调试了yolov3的算法还不知道能不能检测出来。在看一会第六章吧，能看多少看多少。