Simulink入门（三）

1.曲面图的绘制

 

•曲面图的绘制由surf指令完成，该指令的调用格式与mesh指令类似，具体如下：

•（1）surf (X,Y,Z)

•（2）surf (Z)

•（3）surf (X,Y,Z,C)

•（4）surf(X,Y,Z,’PropertyName’,PropertyValue,…)

•与mesh指令不同的是，mesh指令所绘制的图形是网格划分的曲面图，而surf指令绘制得到的是平滑着色的三维曲面图，着色的方式是在得到相应的网格点后，对每一个网格依据该网格所代表的节点的色值（由变量C控制）来定义这一网格的颜色。

 

•采用surf命令实现曲面的绘制，程序如下：

•clc,clear,closeall

•X = -10:1:10; 

•Y = -10:1:10;

•[X,Y] = meshgrid(X,Y);

•Z = - X.^2 - Y.^2 + 10;

•surf(X,Y,Z)

•xlabel('x')

•ylabel('y')

•zlabel('z')

•axis tight

•colormap(jet)

•shading interp

•set(gca,'Ydir','reverse');

•set (gcf, 'color', 'w')

 

 

 

2. 特殊图形绘制

•MATLAB对于不同的三维曲面绘制，提供了不同的画图函数，例如slice切片函数、quiver3三维箭头标记函数、sphere等等，因此MATLAB丰富的图形可视化工具箱函数应用相当广泛。

 

 

•空间曲线及其运动方向的表现，编程如下：

•clc,clear,closeall

•t=0:0.1:1.5;

•Vx=2*t;

•Vy=2*t.^2;

•Vz=6*t.^3-t.^2;

•x=t.^2;

•y=(2/3)*t.^3;

•z=(6/4)*t.^4-(1/3)*t.^3;  %由速度得到曲线

•plot3(x,y,z,'r.-'),       %画飞行轨迹

•hold on  

•%算数值梯度

•Vx=gradient(x);

•Vy=gradient(y);

•Vz=gradient(z);

•quiver3(x,y,z,Vx,Vy,Vz), %画速度矢量图

•grid on       % 栅格化

•xlabel('x')

•ylabel('y')

•zlabel('z')

•

 

3.微积分问题的MATLAB求解

 

•符号变量在解决工程问题中应用较多，对于一个工程问题而言，一般首先从变量出发，把问题用符号变量表示出来（得到符号矩阵），然后通过符号变量求解得到一般表达式，根据该表达式，代入相应的初始条件，即可得到问题的具体的解。

1. 极限

•MATLAB提供了求极限函数limit()，函数调用格式为：y = limit(fun,x,x0)。

•其中，y为返回的函数极限值；

•    fun为要求解的函数；

•     x为函数自变量；

•     x0位函数自变量的取值，x趋近于x0。

•MATLAB求解极限问题有专门的函数，编程如下：

•clc,clear,closeall

•symsx a 

•I1=limit('(sin(x)-sin(3*x))/sin(x)',x,0)

•I2=limit('(tan(x)-tan(a))/(x-a)',x,a)

•I3=limit('(3*x-5)/(x^3*sin(1/x^2))',x,inf)

•运行程序输出结果如下：

•I1 =

•-2

•

•I2 =

•tan(a)^2 + 1

•

•I3 =

•3

•

2.导数

 

•diff是求微分最常用的函数，其输入参数既可以是函数表达式，也可以是符号矩阵。

•MATLAB常用的格式是：diff(f, x, n)；

•其中，f关于x求n阶导数。

•MATLAB求解导数问题，编程如下：

•clc,clear,closeall

•symsx y 

•f=sym('exp(-2*x)*cos(3*x^(1/2))')

•diff(f,x)

•g=sym('g(x,y)')                    %建立抽象函数。

•f=sym('f(x,y,g(x,y))')                %建立复合抽象函数。

•diff(f,x)

•diff(f,x,2)

•运行程序输出结果如下：

•f =

•exp(-2*x)*cos(3*x^(1/2))

•

•ans=

•- 2*exp(-2*x)*cos(3*x^(1/2)) - (3*exp(-2*x)*sin(3*x^(1/2)))/(2*x^(1/2))

•

•

 

 

•g =

•g(x, y)

•

•f =

•f(x, y, g(x, y))

•

•ans=

•D([3], f)(x, y, g(x, y))*diff(g(x, y), x) + D([1], f)(x, y, g(x, y))

•

•ans=

•(D([3, 3], f)(x, y, g(x, y))*diff(g(x, y), x) + D([1, 3], f)(x, y, g(x, y)))*diff(g(x, y), x) + D([1, 3], f)(x, y, g(x, y))*diff(g(x, y), x) + D([3], f)(x, y, g(x, y))*diff(g(x, y), x, x) + D([1, 1], f)(x, y, g(x, y))

•数值求导指令diff，程序如下：

•clc,clear,closeall

•x=linspace(0,2*pi,50);

•y=sin(x);

•dydx=diff(y)./diff(x);

•plot(x(1:49),dydx),grid

•

•MATLAB int()函数是求积分最常用的函数，其输入参数可以是函数表达式。

•常用的格式是：int(f, r, x0, x1)。

•其中，f为所要积分的表达式；

•r为积分变量，若为定积分，则x0与x1为积分上下限。

•求解积分函数int，编写程序如下：

•clc,clear,closeall

•syms   x y z

•I1=int(sin(x*y+z),z)

•I2=int(1/(3+2*x+x^2),x,0,1)

•I3=int(1/(3+2*x+x^2),x,-inf,inf)

•运行程序输出结果如下：

•I1 =

•    -cos(z + x*y)

•I2 =

•    -(2^(1/2)*(atan(8^(1/2)/4) - atan(2^(1/2))))/2

•I3 =

•   (pi*2^(1/2))/2

•

3.  微分方程的数值解

 

 

•求解微积分方程你的数值解常用的MATLAB函数调用如下：

•[t, x] = ode23(‘xprime’, t0, tf, x0, tol, trace)

•[t, x] = ode45(‘xprime’, t0, tf, x0, tol, trace)

•或

•[t, x] = ode23(‘xprime’, [t0, tf], x0, tol, trace)

•[t, x] = ode45(‘xprime’, [t0, tf], x0, tol, trace)

•说明：

•（1）两个指令的调用格式相同，均为Runge-Kutta法。

•（2）该指令是针对一阶常微分设计的。因此，假如待解的是高阶微分方程，那么它必修先演化为形如 的一阶微分方程组，即“状态方程”。

•（3）’xprime’是定义 的函数名。该函数文件必须以 为一个列向量输出，以 为输入参量（注意输入变量之间的 关系，先“时间变量”后“状态变量”）。

•（4）输入参量 和 分别是积分的起始值和终止值。

•（5）输入参量 为初始状态列向量。

•（6）输出参量 和 分别给出“时间”向量和相应的状态向量。

•（7）tol控制解的精度，可缺省。缺省时，ode23默认tol=1.e-3；ode23默认tol=1.e-6。

•（8）输入参量trace控制求解的中间结果是否显示，可缺省，缺省时，默认为tol=0，不显示中间结果。

•（9）一般地，两者分别采用自适应变步长（即当解的变化较慢时采用较大的步长，从而使得计算速度快；当解的变化速度较快时步长会自动地变小，从而使得计算精度更高）的二、三阶Runge-Kutta算法和四、五阶Runge-Kutta算法，ode45比ode23的积分分段少，而运算速度快。

•

 

•

•建立方程组的函数文件如下：

•function dz=dzdx1(x,z)

•dz(1)=z(2);

•dz(2)=z(3);

•dz(3)=z(3)*x^(-1)-3*x^(-2)*z(2)+2*x^(-3)*z(1)+9*x^3*sin(x);

•dz=[dz(1);dz(2);dz(3)];

•end

•编写主程序如下：

•clc,clear,closeall

•H=[0.1,60]; 

•z0=[1;1;1];

•[x,z]=ode15s('dzdx1',H,z0);

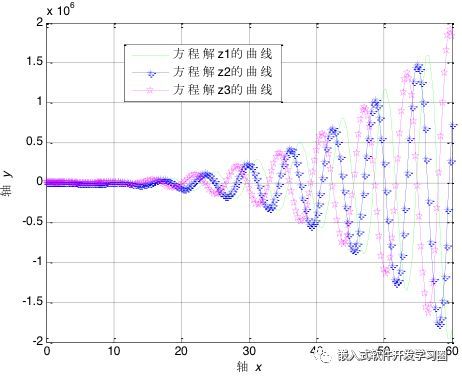
•plot(x,z(:,1),'g--',x,z(:,2),'b*--',x,z(:,3),'mp--')

•xlabel('轴\it x');

•ylabel('轴\it y')

•grid on

•legend('方程解z1的曲线','方程解z2的曲线', '方程解z3的曲线')

•

 

 

4  龙贝格积分法微积分运算

•在MATLAB中编程实现的龙贝格积分法的函数为：[I,step]=Roberg(f,a,b,eps)。

•功能：龙贝格积分法求函数的数值积分。

•调用格式：[I,step]=Roberg(f,a,b,eps)。

•其中，I:积分值；

•step: 积分划分的子区间次数；

•f: 函数名；

•a: 积分下限；

•b: 积分上限；

•eps: 积分精度；

•

5.  有限差分方法求边值问题

•在MATLAB中编程实现的有限差分方法的函数为：

•[k,A,B1,X,Y,y,wucha,p]=yxcf(q1,q2,q3,a,b,alpha,beta,h)

•功能：有限差分方法求函数的边值问题。

•调用格式：[k,A,B1,X,Y,y,wucha,p]=yxcf(q1,q2,q3,a,b,alpha,beta,h)。

•其中，q1、q2、q3：方程系数；

•a为方程y的初始化值x0；

•b为方程y的区间终值xn；

•alpha为y(a)对应的值；

•beta为y(b)对应的值；

•h为求解步长；

•k为计算迭代步数；

•A为矩阵系数；

•B1为矩阵系数；

•Y为矩阵向量；

•y为求解目标方程的边值；

•wucha为求解误差；

•p等于[k',X',y,wucha']，为一个矩阵；

•

6.  样条函数求积分

 

•MATLAB中的样条工具箱中提供了求样条函数的积分的函数fnint。函数fnint的常见用法如下：

•q=fnint(Y)

•它表示求取样条函数Y的积分。

•在用函数fnint求积分之前，必须用样条工具箱中的函数csape对被积分函数进行样条插值拟合。

•

7.  常微分方程符号解

•MATLAB常微分方程符号解的语法是：

•dsolve('equation','condition')

•其中，equation代表常微分方程式即y'= g(x,y)，且须以Dy代表一阶微分项y'，D2y代表二阶微分项y''，condition则为初始条件。

•函数dsolve用来解符号常微分方程、方程组，如果没有初始条件，则求出通解，如果有初始条件，则求出特解。

•dsolve的调用格式如下：

•（1）dsolve('equation')  %给出微分方程的解析解，表示为t的函数；

•（2）dsolve('equation', 'condition')  %给出微分方程初值问题的解，表示为t的函数；

•（3）dsolve('equation', 'v')  %给出微分方程的解析解，表示为v的函数；

•（4）dsolve('equation', 'condition', 'v')  %给出微分方程初值问题的解，表示为v的函数。

•

 

8.非线性方程组求解

 

•函数：fsolve

•格式如下：

•x = fsolve(fun,x0)  %用fun定义向量函数，其定义方式为：先定义方程函数function F = myfun(x)。

•F =[表达式1；表达式2；…表达式m]  %保存为myfun.m，并用下面方式调用：x = fsolve(@myfun,x0)，x0为初始估计值。

•x = fsolve(fun,x0,options)

•[x,fval] = fsolve(…)    %fval=F(x)，即函数值向量

•[x,fval,exitflag] = fsolve(…)

•[x,fval,exitflag,output] = fsolve(…)

•[x,fval,exitflag,output,jacobian] = fsolve(…)  % jacobian为解x处的Jacobian阵。

•

 

 

 

•MATLAB中利用函数fminsearch求无约束多元函数最小值。

•函数：fminsearch

•格式如下：

•x = fminsearch(fun,x0)  %x0为初始点，fun为目标函数的表达式字符串或MATLAB自定义函数的函数柄。

•x = fminsearch(fun,x0,options)   % options查optimset

•[x,fval] = fminsearch(…)  %最优点的函数值

•[x,fval,exitflag] = fminsearch(…)  % exitflag与单变量情形一致

•[x,fval,exitflag,output] = fminsearch(…) %output与单变量情形一致

•注意：fminsearch采用了Nelder-Mead型简单搜寻法。

•

9.无约束最优化问题求解

 

•MATLAB中利用函数fminsearch求无约束多元函数最小值。

•函数：fminsearch

•格式如下：

•x = fminsearch(fun,x0)  %x0为初始点，fun为目标函数的表达式字符串或MATLAB自定义函数的函数柄。

•x = fminsearch(fun,x0,options)   % options查optimset

•[x,fval] = fminsearch(…)  %最优点的函数值

•[x,fval,exitflag] = fminsearch(…)  % exitflag与单变量情形一致

•[x,fval,exitflag,output] = fminsearch(…) %output与单变量情形一致

•注意：fminsearch采用了Nelder-Mead型简单搜寻法。

•

10.线性规划问题.

•线性规划问题是目标函数和约束条件均为线性函数的问题，在MATLAB 2013a版中，线性规划问题（Linear Programming）已用函数linprog取代了MATLAB 7.0版中的lp函数。当然，由于版本的向下兼容性，一般说来，低版本中的函数在高版中仍可使用。

•函数：linprog

•格式如下：

•x = linprog(f,A,b)  %求min    

•x = linprog(f,A,b,Aeq,beq)  %等式约束，若没有不等式约束，则A=[ ]，b=[ ]。

•x = linprog(f,A,b,Aeq,beq,lb,ub)  %指定x的范围，若没有等式约束  ，则Aeq=[ ]，beq=[ ]

•x = linprog(f,A,b,Aeq,beq,lb,ub,x0)   %设置初值x0

•x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)    % options为指定的优化参数

•[x,fval] = linprog(…)  % 返回目标函数最优值，即。

•[x,lambda,exitflag] = linprog(…)  % lambda为解的Lagrange乘子。

•[x, lambda,fval,exitflag] = linprog(…)  % 终止迭代的错误条件。

•[x,fval, lambda,exitflag,output] = linprog(…)  % output为关于优化的一些信息

•说明：若表示函数收敛于解，表示超过函数估值或迭代的最大数字，表示函数不收敛于解；若lambda=lower表示下界，lambda=upper表示上界ub，lambda=ineqlin表示不等式约束，lambda=eqlin表示等式约束，lambda中的非0元素表示对应的约束是有效约束；output=iterations表示迭代次数，output=algorithm表示使用的运算规则，output=cgiterations表示PCG迭代次数。

•

11.二次型规划问题.

 

•MATLAB 2014a版中的函数quadprog用来解决二次规划问题（quadratic programming）问题，且已经取代了低版本MATLABqp函数。

•函数：quadprog

•格式如下：

•x = quadprog(H,f,A,b)  %其中、、、为标准形中的参数，x为目标函数的最小值。

•x = quadprog(H,f,A,b,Aeq,beq)    %Aeq, beq满足等约束条件。

•x = quadprog(H,f,A,b,Aeq,beq,lb,ub)    % lb, ub分别为解x的下界与上界。

•x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)    %x0为设置的初值

•x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)     % options为指定的优化参数

•[x,fval] = quadprog(…)    %fval为目标函数最优值

•[x,fval,exitflag] = quadprog(…)    % exitflag与线性规划中参数意义相同

•[x,fval,exitflag,output] = quadprog(…)    % output与线性规划中参数意义相同

•[x,fval,exitflag,output,lambda] = quadprog(…)   % lambda与线性规划中参数意义相同

•