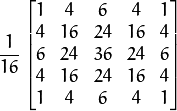OpenCV常用库函数

一、core 模块

1、Mat - 基本图像容器

        Mat 是一个类，由两个数据部分组成：矩阵头（包含矩阵尺寸，存储方法，存储地址等信息）和一个指向存储所有像素值的矩阵（根据所选存储方法的不同矩阵可以是不同的维数）的指针。

        创建Mat对象方法：

1->Mat() 构造函数:
Mat M(2,2, CV_8UC3, Scalar(0,0,255)); 
int sz[3] = {2,2,2}; 
Mat L(3,sz, CV_8UC(1), Scalar::all(0));
2->Create() function: 函数
M.create(4,4, CV_8UC(2));
3-> 初始化zeros(), ones(), :eyes()矩阵
Mat E = Mat::eye(4, 4, CV_64F);  
Mat O = Mat::ones(2, 2, CV_32F); 
Mat Z = Mat::zeros(3,3, CV_8UC1);
4->用逗号分隔的初始化函数:
Mat C = (Mat_(3,3) << 0, -1, 0, -1, 5, -1, 0, -1, 0); 

         常用操作：

Mat A, C;                                 // 只创建信息头部分
A = imread(argv[1], CV_LOAD_IMAGE_COLOR); // 这里为矩阵开辟内存
Mat B(A);                                 // 使用拷贝构造函数
C = A;                                    // 赋值运算符
Mat D (A, Rect(10, 10, 100, 100) ); // using a rectangle
Mat E = A(Range:all(), Range(1,3)); // using row and column boundaries
Mat F = A.clone();
Mat G;
A.copyTo(G);                       //使用函数 clone() 或者 copyTo() 来拷贝一副图像的矩阵。

2、图像基本操作（Mat操作）

2.1 滤波器掩码

滤波器在图像处理中的应用广泛，OpenCV也有个用到了滤波器掩码（也称作核）的函数。使用这个函数，你必须先定义一个表示掩码的 Mat 对象：

Mat kern = (Mat_(3,3) <<  0, -1,  0,
                               -1,  5, -1,
                                0, -1,  0);
filter2D(I, K, I.depth(), kern );  

2.2 图像混合（addWeighted函数）

 线性混合操作 也是一种典型的二元（两个输入）的 像素操作 ：

通过在范围  内改变  ，这个操可以用来对两幅图像或两段视频产生时间上的 画面叠化 （cross-dissolve）效果。

alpha = 0.3；
beta = ( 1.0 - alpha );
addWeighted( src1, alpha, src2, beta, 0.0, dst);

2.3 改变图像的对比度和亮度

• 两种常用的点过程（即点算子），是用常数对点进行 乘法 和 加法 运算：

  

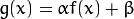
• 两个参数 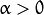 和 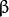 一般称作 增益 和 偏置 参数。我们往往用这两个参数来分别控制 对比度 和 亮度 。

• 你可以把 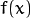 看成源图像像素，把  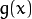看成输出图像像素。这样一来，上面的式子就能写得更清楚些：

  

  其中，  和 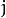 表示像素位于 第i行 和 第j列 。

double alpha;
int beta;
Mat image = imread( argv[1] );
Mat new_image = Mat::zeros( image.size(), image.type() );
for( int y = 0; y < image.rows; y++ )
{
    for( int x = 0; x < image.cols; x++ )
    {
        for( int c = 0; c < 3; c++ )
        {
            new_image.at(y,x)[c] = saturate_cast( alpha*( image.at(y,x)[c] ) + beta );
        }
    }
}

2.4 离散傅立叶变换

    对一张图像使用傅立叶变换就是将它分解成正弦和余弦两部分。也就是将图像从空间域(spatial domain)转换到频域(frequency domain)。  2维图像的傅立叶变换可以用以下数学公式表达:
                                                 
式中 f 是空间域(spatial domain)值， F 则是频域(frequency domain)值。

Mat padded;          //将输入图像延扩到最佳的尺寸
int m = getOptimalDFTSize( I.rows );
int n = getOptimalDFTSize( I.cols ); // 在边缘添加0
copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));
Mat planes[] = {Mat_(padded), Mat::zeros(padded.size(), CV_32F)};
Mat complexI;
merge(planes, 2, complexI);         // 为延扩后的图像增添一个初始化为0的通道
dft(complexI, complexI);            // 变换结果很好的保存在原始矩阵中
split(complexI, planes);                   // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude
Mat magI = planes[0];

2.5 基本绘图

Point:
	Point pt;
	pt.x = 10;
	pt.y = 8;
	或者
	Point pt =  Point(10, 8);

Scalar:
	Scalar( B, G, R )   //定义的RGB颜色值为：Blue,Green, Red
	
line 绘直线:
	line( img,   //输出图像
        start,   //起始点
        end,     //结束点
        Scalar( 0, 0, 0 ),  //颜色
        thickness=2,    //线条粗细
        lineType=8 );   //线条类型

ellipse 绘椭圆：
	ellipse( img,   //输出图像
           Point( w/2.0, w/2.0 ),   //中心为点 (w/2.0, w/2.0) 
           Size( w/4.0, w/16.0 ),     //大小位于矩形 (w/4.0, w/16.0) 内
           angle,    //旋转角度为 angle
           0,
           360,     //扩展的弧度从 0 度到 360 度
           Scalar( 255, 0, 0 ),   //颜色
           thickness,   //线条粗细
           lineType );    //线条类型

circle 绘圆：
	circle( img,   //输出图像
         center,    //圆心由点 center 定义
         w/32.0,     /圆的半径为: w/32.0
         Scalar( 0, 0, 255 ),   //颜色
         thickness,   //线条粗细
         lineType );   //线条类型
		 
rectangle 绘矩形：
	rectangle( rook_image,
           Point( 0, 7*w/8.0 ),
           Point( w, w),    //矩形两个对角顶点为 Point( 0, 7*w/8.0 ) 和 Point( w, w)
           Scalar( 0, 255, 255 ),
           thickness = -1,
           lineType = 8 );

fillPoly 绘填充的多边形：
	fillPoly( img,
            ppt,   //多边形的顶点集为 ppt
            npt,   //要绘制的多边形顶点数目为 npt
            1,   //要绘制的多边形数量仅为 1
            Scalar( 255, 255, 255 ),
            lineType );

2.6 随机数发生器

    RNG的实现了一个随机数发生器。 在上面的例子中, rng 是用数值 0xFFFFFFFF 来实例化的一个RNG对象。

RNG rng( 0xFFFFFFFF );  

二、imgproc 模块

1、图像平滑处理

    平滑也称模糊, 平滑处理时需要用到一个 滤波器 。 最常用的滤波器是 线性 滤波器，线性滤波处理的输出像素值 (i.e. ) 是输入像素值 (i.e. )的加权和 :

 称为 核, 它仅仅是一个加权系数。

不妨把 滤波器 想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口滑过图像。

1.1 归一化块滤波器 (Normalized Box Filter)

blur( src,    //输入图像
      dst,    //输出图像
      Size( i, i ),    //定义内核大小( w 像素宽度， h 像素高度)
      Point(-1,-1))    //指定锚点位置(被平滑点)， 如果是负值，取核的中心为锚点。

1.2 高斯滤波器 (Gaussian Filter)

GaussianBlur( src,    //输入图像
             dst,     //输出图像
             Size( i, i ),    //定义内核的大小(需要考虑的邻域范围)。  w 和 h 必须是正奇数，否则将使用  和  参数来计算内核大小。
             0,    //: x 方向标准方差， 如果是 0 则  使用内核大小计算得到。
             0 )    //: y 方向标准方差， 如果是 0 则  使用内核大小计算得到。

1.3 中值滤波器 (Median Filter)

medianBlur ( src,   //输入图像
             dst,    //输出图像
             i );    //内核大小 (只需一个值，因为我们使用正方形窗口)，必须为奇数。

1.4 双边滤波 (Bilateral Filter)

bilateralFilter ( src,  //输入图像
 dst,    //输出图像
 i,     //像素的邻域直径
 i*2,    //: 颜色空间的标准方差
 i/2 );    //: 坐标空间的标准方差(像素单位)

2、形态学变换

    形态学操作就是基于形状的一系列图像处理操作。最基本的形态学操作有二：腐蚀与膨胀(Erosion 与 Dilation)。 他们的运用广泛:

• 消除噪声
• 分割(isolate)独立的图像元素，以及连接(join)相邻的元素。
• 寻找图像中的明显的极大值区域或极小值区域。

2.1 腐蚀（Erosion）

     此操作将图像 A 与任意形状的内核 B（通常为正方形或圆形）进行卷积，将内核 B 覆盖区域的最小相素值提取，并代替锚点位置的相素。这一操作将会导致图像中的亮区开始“收缩”。

erode(  src,   //原图像
        erosion_dst,    //输出图像
        element );   //腐蚀操作的内核，默认为一个简单的 3x3 矩阵。也可以使用函数 getStructuringElement。
Mat element = getStructuringElement( erosion_type,
                                     Size( 2*erosion_size + 1, 2*erosion_size+1 ),
                                     Point( erosion_size, erosion_size ) );

2.2 膨胀 (Dilation)

    此操作将图像 A 与任意形状的内核 B（通常为正方形或圆形）进行卷积，将内核 B 覆盖区域的最大相素值提取，并代替锚点位置的相素。这一操作将会导致图像中的亮区开始“扩展”。

ditale( src,   //原图像
        dilate_dst,    //输出图像
        element );   //腐蚀操作的内核，默认为一个简单的 3x3 矩阵。也可以使用函数 getStructuringElement。
Mat element = getStructuringElement( dilation_type,
                                     Size( 2*dilation_size + 1, 2*dilation_size+1 ),
                                     Point( dilation_size, dilation_size ) );

2.3 开运算 (Opening)

    开运算是通过先对图像腐蚀再膨胀实现的。能够排除小团块物体(假设物体较背景明亮)。

    

2.4 闭运算(Closing)

    闭运算是通过先对图像膨胀再腐蚀实现的。能够排除小型黑洞(黑色区域)。

    

2.5 形态梯度(Morphological Gradient)

    膨胀图与腐蚀图之差。能够保留物体的边缘轮廓。

    

2.6 顶帽(Top Hat)

    原图像与开运算结果图之差。

    

2.7 黑帽(Black Hat)

    闭运算结果图与原图像之差

    

3、图像金字塔

    一个图像金字塔是一系列图像的集合 - 所有图像来源于同一张原始图像 - 通过梯次向下采样获得，直到达到某个终止条件才停止采样。有两种类型的图像金字塔常常出现在文献和应用中:
            高斯金字塔(Gaussian pyramid): 用来向下采样

            拉普拉斯金字塔(Laplacian pyramid): 用来从金字塔低层图像重建上层未采样图像

用如下方法向上采样:

• 将 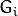 与高斯内核卷积:

  

• 将所有偶数行和列去除。

pyrUp( tmp, dst, Size( tmp.cols*2, tmp.rows*2 ) );

对图像的向下采样：

• 将图像在每个方向扩大为原来的两倍，新增的行和列以0填充()
• 使用先前同样的内核(乘以4)与放大后的图像卷积，获得 “新增像素” 的近似值。

pyrDown( tmp, dst, Size( tmp.cols/2, tmp.rows/2 ) );

4、阈值操作

   最简单的图像分割的方法。 例如：可以将该物体的像素点的灰度值设定为：‘0’（黑色）,其他的像素点的灰度值为：‘255’（白色）；当然像素点的灰度值可以任意，但最好设定的两种颜色对比度较强，方便观察结果

threshold( src_gray,    //输入的灰度图像
 dst,   //输出图像
 threshold_value,   //进行阈值操作时阈值的大小
 max_BINARY_value,   //设定的最大灰度值
 threshold_type );  // 阈值的类型。
                     0: 二进制阈值
                     1: 反二进制阈值
                     2: 截断阈值
                     3: 0阈值
                     4: 反0阈值

5、给图像添加边界

    图像的卷积操作中，处理卷积边缘时需要考虑边缘填充。

copyMakeBorder( src, 
		dst, 
		top,bottom, left,right, //各边界的宽度
		borderType,     //边界类型，可选择常数边界BORDER_CONSTANT或者复制边界BORDER_REPLICATE。
		value );    //如果 borderType 类型是 BORDER_CONSTANT, 该值用来填充边界像素。

6、图像卷积

6.1 函数 filter2D 就可以生成滤波器

filter2D(src,
         dst,
         ddepth,   //dst 的深度。若为负值（如 -1 ），则表示其深度与源图像相等。
         kernel,   //用来遍历图像的核
         anchor,   //核的锚点的相对位置，其中心点默认为 (-1, -1) 。
         delta,   //在卷积过程中，该值会加到每个像素上。默认情况下，这个值为 0 。
         BORDER_DEFAULT );   //默认即可

6.2 Sobel 导数

    Sobel 算子用来计算图像灰度函数的近似梯度。Sobel 算子结合了高斯平滑和微分求导。

       计算：

1. 在两个方向求导:

   1. 水平变化: 将  与一个奇数大小的内核  进行卷积。比如，当内核大小为3时,  的计算结果为:

      

   2. 垂直变化: 将:math:I 与一个奇数大小的内核  进行卷积。比如，当内核大小为3时,  的计算结果为:

      

2. 在图像的每一点，结合以上两个结果求出近似 梯度:

   

   有时也用下面更简单公式代替:

   

  /// 求 X方向梯度
  //Scharr( src_gray, grad_x, ddepth, x_order=1, y_order=0, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_x, ddepth, x_order=1, y_order=0, 3, scale, delta, BORDER_DEFAULT );  
  convertScaleAbs( grad_x, abs_grad_x );       //将中间结果转换到 CV_8U

  /// 求Y方向梯度
  //Scharr( src_gray, grad_y, ddepth, x_order=0, y_order=1, scale, delta, BORDER_DEFAULT );
  Sobel( src_gray, grad_y, ddepth, x_order=0, y_order=1, 3, scale, delta, BORDER_DEFAULT );
  convertScaleAbs( grad_y, abs_grad_y );

  /// 合并梯度(近似)
  addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

6.3 Laplace 算子

1. 二阶导数可以用来 检测边缘。 因为图像是 “2维”, 我们需要在两个方向求导。使用Laplacian算子将会使求导过程变得简单。
2. Laplacian 算子 的定义:

Laplacian( src_gray,
           dst,
           ddepth,        //输出图像的深度。 因为输入图像的深度是 CV_8U 
           kernel_size,   //内部调用的 Sobel算子的内核大小
           scale,
           delta,
           BORDER_DEFAULT );

6.4 Canny 边缘检测

    Canny 使用了滞后阈值，滞后阈值需要两个阈值(高阈值和低阈值):

1.     如果某一像素位置的幅值超过 高 阈值, 该像素被保留为边缘像素。
2.     如果某一像素位置的幅值小于 低 阈值, 该像素被排除。
3.     如果某一像素位置的幅值在两个阈值之间,该像素仅仅在连接到一个高于 高 阈值的像素时被保留。

            Canny 推荐的 高:低 阈值比在 2:1 到3:1之间

Canny(   detected_edges,   //原灰度图像
         detected_edges,   //输出图像
         lowThreshold,   //低阈值
         lowThreshold*ratio,   //设定为低阈值的3倍 (根据Canny算法的推荐)
         kernel_size );   //设定为 3 (Sobel内核大小，内部使用)

6.5 霍夫线变换

1. 霍夫线变换是一种用来寻找直线的方法.
2. 是用霍夫线变换之前, 首先要对图像进行边缘检测的处理，也即霍夫线变换的直接输入只能是边缘二值图像.

Canny(src, dst, 50, 200, 3);  //用Canny算子对图像进行边缘检测
vector lines;
/*标准霍夫线变换*/
HoughLines(  dst,
             lines,   //储存着检测到的直线的参数对 (r,\theta) 的容器
             rho=1,     //参数极径 rho 以像素值为单位的分辨率. 
             CV_PI/180,   //参数极角 \theta 以弧度为单位的分辨率. 我们使用 1度 (即CV_PI/180)
             threshold=100,
             0,0 );    //srn and stn: 参数默认为0. 
//通过画出检测到的直线来显示结果. 
for( size_t i = 0; i < lines.size(); i++ )
{
  float rho = lines[i][0], theta = lines[i][1];
  Point pt1, pt2;
  double a = cos(theta), b = sin(theta);
  double x0 = a*rho, y0 = b*rho;
  pt1.x = cvRound(x0 + 1000*(-b));
  pt1.y = cvRound(y0 + 1000*(a));
  pt2.x = cvRound(x0 - 1000*(-b));
  pt2.y = cvRound(y0 - 1000*(a));
  line( cdst, pt1, pt2, Scalar(0,0,255), 3, CV_AA);
}
 
 /*统计概率霍夫线变换*/
vector lines;
HoughLinesP( dst,
             lines,   //储存着检测到的直线的参数对 (x_{start}, y_{start}, x_{end}, y_{end}) 的容器
             rho=1,    //参数极径 rho 以像素值为单位的分辨率. 
             CV_PI/180,
             threshold=50,   //要”检测” 一条直线所需最少的的曲线交点 
             minLinLength=50,   //能组成一条直线的最少点的数量. 点数量不足的直线将被抛弃.
             maxLineGap=10 );   //能被认为在一条直线上的亮点的最大距离.
//通过画出检测到的直线来显示结果.
for( size_t i = 0; i < lines.size(); i++ )
{
  Vec4i l = lines[i];
  line( cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0,0,255), 3, CV_AA);
}

6.6 霍夫圆变换

       霍夫圆变换的基本原理和上个教程中提到的霍夫线变换类似, 只是点对应的二维极径极角空间被三维的圆心点x, y还有半径r空间取代.

GaussianBlur( src_gray, src_gray, Size(9, 9), 2, 2 );   //高斯模糊以降低噪声
vector circles;
HoughCircles( src_gray,   //输入图像 (灰度图)
              circles,   //存储下面三个参数: x_{c}, y_{c}, r 集合的容器来表示每个检测到的圆.
              CV_HOUGH_GRADIENT,   //指定检测方法. 现在OpenCV中只有霍夫梯度法
              dp = 1,   //累加器图像的反比分辨率
              min_dist = src_gray.rows/8,   //检测到圆心之间的最小距离
              param_1 = 200,    //   //圆心检测阈值.
              param_2 = 100,      //圆心检测阈值.
              0,    //能检测到的最小圆半径,默认为0. 
              0 );   //能检测到的最大圆半径, 默认为0
//绘出检测到的圆
for( size_t i = 0; i < circles.size(); i++ )
{
   Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
   int radius = cvRound(circles[i][2]);
   // circle center
   circle( src, center, 3, Scalar(0,255,0), -1, 8, 0 );
   // circle outline
   circle( src, center, radius, Scalar(0,0,255), 3, 8, 0 );
}

7、 Remapping 重映射

    把一个图像中一个位置的像素放置到另一个图片指定位置的过程。

    我们通过重映射来表达每个像素的位置  :

 remap(  src,
         dst,
         map_x,   // x方向的映射参数. 它相当于方法 h(i,j) 的第一个参数
         map_y,   //y方向的映射参数. 注意 map_y 和 map_x 与 src 的大小一致。
         CV_INTER_LINEAR,  //非整数像素坐标插值标志. 这里给出的是默认值(双线性插值).
         BORDER_CONSTANT,   // 默认
         Scalar(0,0, 0) );

8、 仿射变换

    一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).    

    使用  矩阵来表示仿射变换.

 考虑到我们要使用矩阵  和  对二维向量  做变换, 所以也能表示为下列形式:

                                                                or 

//映射的三个点来定义仿射变换:
srcTri[0] = Point2f( 0,0 );
srcTri[1] = Point2f( src.cols - 1, 0 );
srcTri[2] = Point2f( 0, src.rows - 1 );

dstTri[0] = Point2f( src.cols*0.0, src.rows*0.33 );
dstTri[1] = Point2f( src.cols*0.85, src.rows*0.25 );
dstTri[2] = Point2f( src.cols*0.15, src.rows*0.7 );

//getAffineTransform 来求出仿射变换
warp_mat = getAffineTransform( srcTri, dstTri );
warpAffine(  src, 
             warp_dst,
             warp_mat,   //仿射变换矩阵
             warp_dst.size() );   //输出图像的尺寸

9、 直方图均衡化

    直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法.

equalizeHist( src, dst );

10、模板匹配

matchTemplate( img, templ, result, match_method );

三、feature2d 模块. 2D特征框架

图像特征类型:

•         边缘
•         角点 (感兴趣关键点)
•         斑点(Blobs) (感兴趣区域)

1、Harris 角点检测子

cornerHarris( src_gray,
             dst,
             blockSize=2,
             apertureSize=3,
             k=0.04,
             BORDER_DEFAULT );
/// Normalizing
normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
convertScaleAbs( dst_norm, dst_norm_scaled );

/// Drawing a circle around corners
for( int j = 0; j < dst_norm.rows ; j++ )
     { for( int i = 0; i < dst_norm.cols; i++ )
          {
            if( (int) dst_norm.at(j,i) > thresh )
              {
               circle( dst_norm_scaled, Point( i, j ), 5,  Scalar(0), 2, 8, 0 );
              }
          }
      }
	/// Showing the result
	namedWindow( corners_window, CV_WINDOW_AUTOSIZE );
	imshow( corners_window, dst_norm_scaled );
}

2、Shi-Tomasi角点检测子

/// Apply corner detection
goodFeaturesToTrack( src_gray,
               corners,
               maxCorners,
               qualityLevel,
               minDistance,
               Mat(),
               blockSize,
               useHarrisDetector,
               k );

/// Draw corners detected
cout<<"** Number of corners detected: "<

3、特征点检测

//--Detect the keypoints using SURF Detector
  int minHessian = 400;

  SurfFeatureDetector detector( minHessian );

  std::vector keypoints_1, keypoints_2;

  detector.detect( img_1, keypoints_1 );
  detector.detect( img_2, keypoints_2 );

 //-- Draw keypoints
  Mat img_keypoints_1; Mat img_keypoints_2;

  drawKeypoints( img_1, keypoints_1, img_keypoints_1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
  drawKeypoints( img_2, keypoints_2, img_keypoints_2, Scalar::all(-1), DrawMatchesFlags::DEFAULT );

 //-- Show detected (drawn) keypoints
  imshow("Keypoints 1", img_keypoints_1 );
  imshow("Keypoints 2", img_keypoints_2 );