基于最大堆实现的优先队列
文章目录
- 最大堆(MaxHeap)是个啥?
- 二叉树的另一种存储结构
- 最大堆的 Sift Up 操作
- 最大堆的 Sift Down 操作
- 最大堆的 Replace 操作
- 最大堆的 Heapify 操作
- 利用 Comparator 实现一个最小堆
- 优先队列的基础知识
- 全部实现代码
- 最大堆
- 最小堆
- 优先队列
最大堆(MaxHeap)是个啥?
最大堆是一颗完全二叉树,最大堆同时也属于二叉堆,下面是就是一个简单的最大堆的树形结构图:
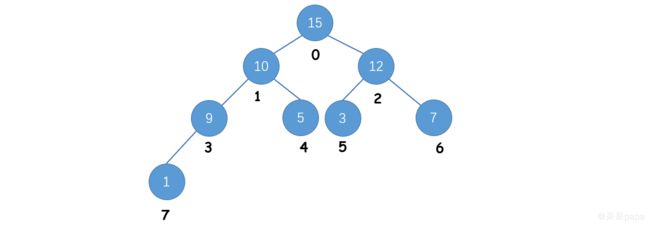
Tip: 最大堆特点,每颗子树根结点所表示的数据值总是大于孩子结点的数据值。
二叉树的另一种存储结构
二叉树也同样有两种存储结构:链式存储和顺序存储。在实现一颗二分搜索树时,采用的是链式存储;而实现一个二叉堆需要使用的就是顺序存储。
为什么要使用顺序存储呢?对于一颗完全二叉树,如果给这棵树进行一个层序编号(从 0 开始),它会是下面这个样子:
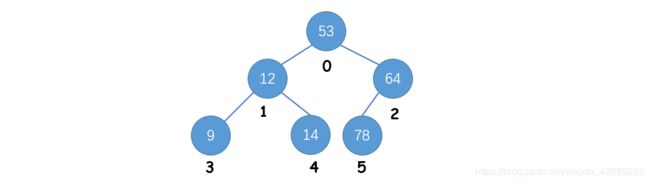
采用层序遍历,相当于按照层序编号遍历一个数组。所以,直接将完全二叉树存入数组还是比较方便的,同时,这样每一个结点也符合二叉树的性质。
Tip: 这里虽然是从 0 开始编号,但是依然满足二叉树的性质,i=0 时,该结点为根结点;i>0 时,该结点的双亲结点为 (i-1) / 2;如 2i + 1 > n,则结点没有左孩子;如 2i + 1 <= n,结点 i 的左孩子为 2i + 1;如 2i + 2 > n,则结点没有右孩子;如 2i + 2 <= n,结点 i 的右孩子为 2i + 2 。
如果将一个普通的二叉树存入一个数组,为了满足二叉树的这个性质,我们就需要借助空结点:
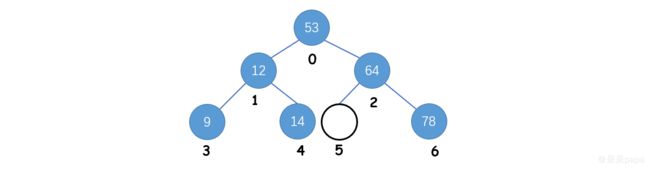
这样做的结果就会导致数组空间的浪费,采用链式存储会更好。
最大堆的 Sift Up 操作
Sift Up 操作是在最大堆插入元素时保证最大堆特性发生的,从而使新插入的结点不断上浮至比它小的双亲结点。
假设一个最大堆中已经有了 [12, 9, 7, 1, 5, 3] 这几个结点,继续向堆中添加 15 和 10 两个结点:

算法思路:
Ⅰ. 将新结点和该结点的双亲结点进行比较
Ⅱ. 如果该结点大于双亲结点,则将两个结点进行交换,继续和双亲结点进行比较
Ⅲ. 如果结点上浮至根结点或则结点小于双亲结点,则停止上浮
public void add(E e) {
if(data.contains(e))
return;
data.add(e);
siftUp(getSize() - 1);
}
private void siftUp(int idx) {
while(idx > 0 && data.get(parent(idx)).compareTo(data.get(idx)) < 0) {
swap(idx, parent(idx));
idx = parent(idx);
}
}
时间复杂度分析: siftUp 操作的时间复杂度为 O(log n);add 操作的时间复杂度为 O(nlog n)
最大堆的 Sift Down 操作
Sift Down 操作发生在从二叉堆中取出元素时保持最大堆特性发生的,将结点下沉到其最大的孩子结点中。
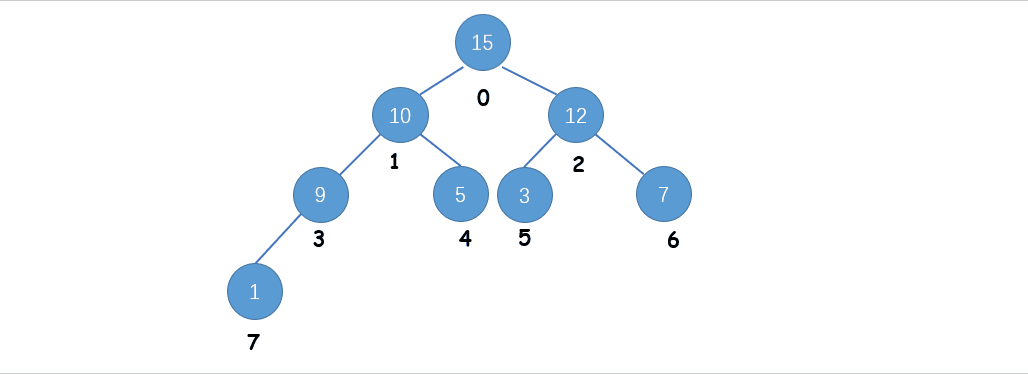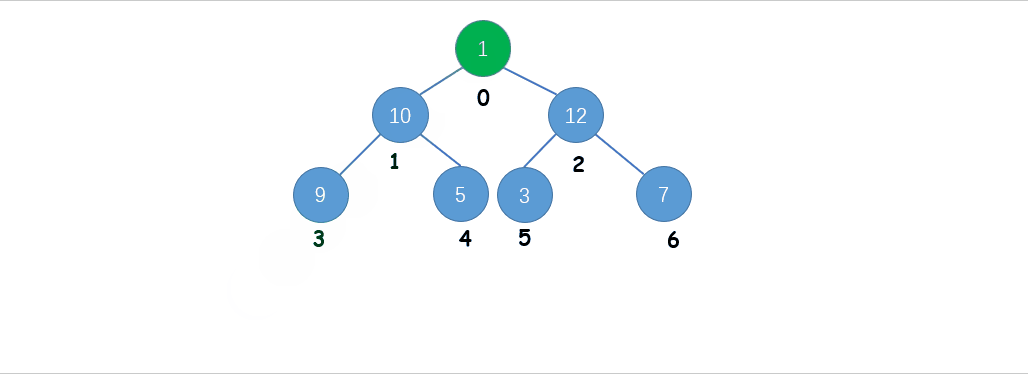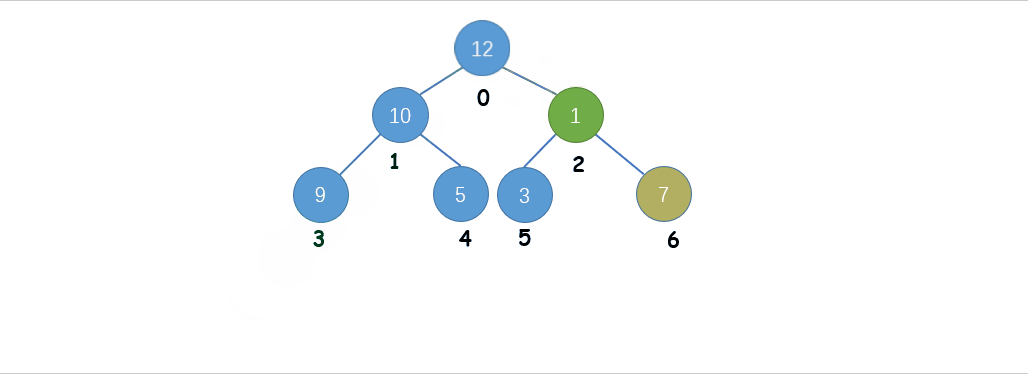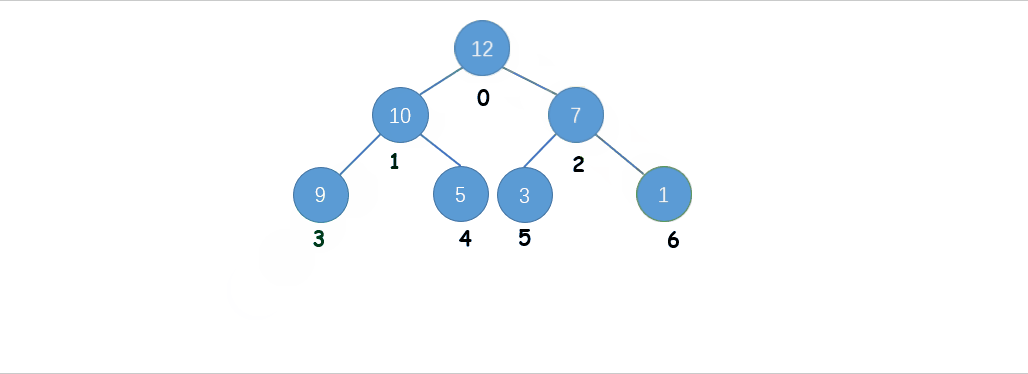
假设从二叉堆 [15, 10, 12, 9, 5, 3, 7, 1] 中取出根结点 15 ,其中发生的下沉过程如下:
Ⅰ. 先取出根结点,然后将最后一个叶子结点移至根结点
Ⅱ. 将根结点和其孩子结点中的最大结点进行比较
Ⅲ. 如果结点小于孩子结点中的最大结点,进行下沉操作,将该结点下沉至孩子结点
Ⅳ. 继续对该结点进行下沉操作,直至该结点大于孩子结点,则停止下沉
public E deleteMax() {
E ret = findMax();
swap(0,data.size()-1);
data.remove(data.size()-1);
siftDown(0);
return ret;
}
private void siftDown(int idx) {
while(leftChild(idx) < data.size()) {
int max = leftChild(idx);
if(leftChild(idx)+1 < data.size() && data.get(leftChild(idx)).compareTo(data.get(rightChild(idx))) < 0) {
max = rightChild(idx);
}
if(data.get(idx).compareTo(data.get(max)) < 0) {
swap(idx, max);
idx = max;
}else {
break;
}
}
}
时间复杂度分析: siftDown 操作的时间复杂度为 O(log n);deleteMax 操作的时间复杂度为 O(log n)
最大堆的 Replace 操作
假设将堆中最大的元素取出,并添加一个新的元素,有两种实现方式:1. 先取出最大元素(调用deleteMax 方法),然后再添加新的结点(调用 add 方法),这种方式会引起一次下沉和一次上浮操作; 2. 使用 Replace 操作,将最大元素替换为新结点,只进行一次下沉操作。
public E replace(E e) {
E ret = data.get(0);
data.set(0, e);
siftDown(0);
return ret;
}
时间复杂度分析: replace 操作的时间复杂度为 O(long n)
最大堆的 Heapify 操作
Heapify 操作的目的是将一个数组转换为最大堆,虽然 add 操作也可以完成操作,但是 Heapify 操作优于 add 操作。
假设使用 Heapify 操作将数组 [1, 5, 3, 9, 12, 7, 15, 10] 转换为最大堆,具体的过程如下:
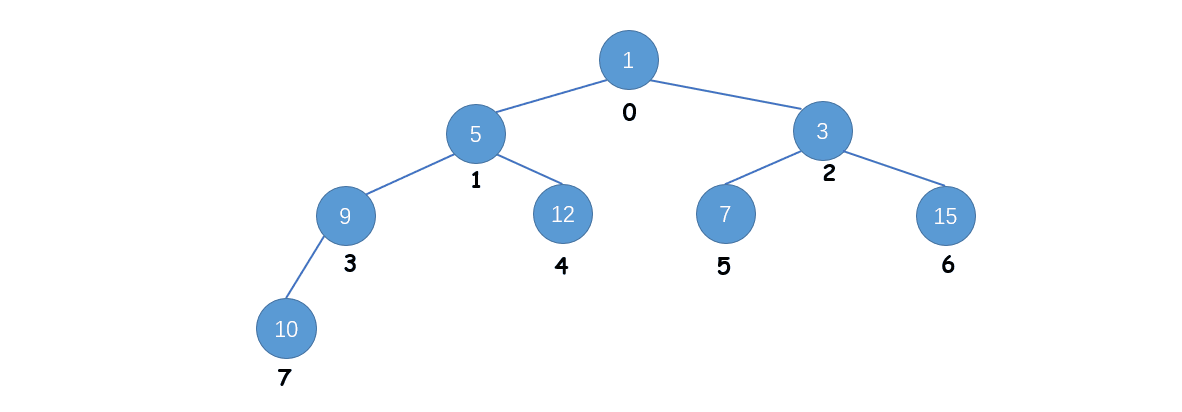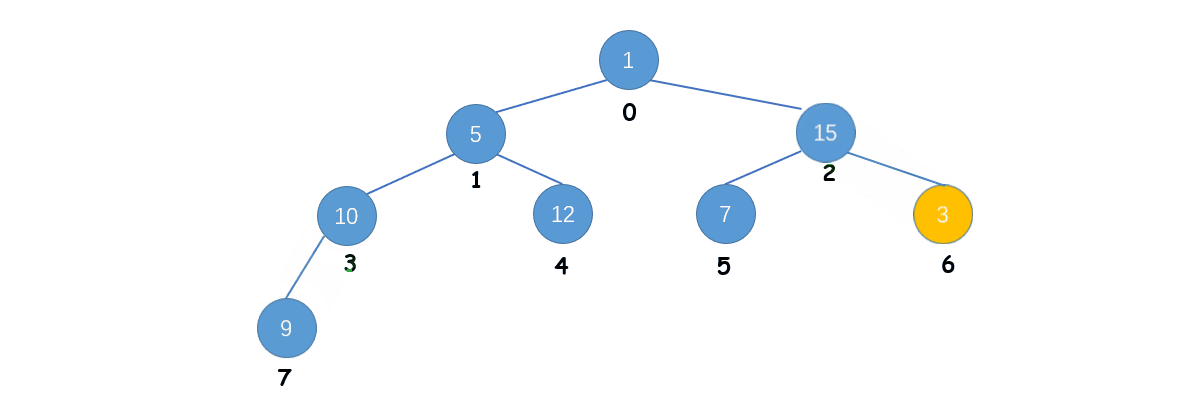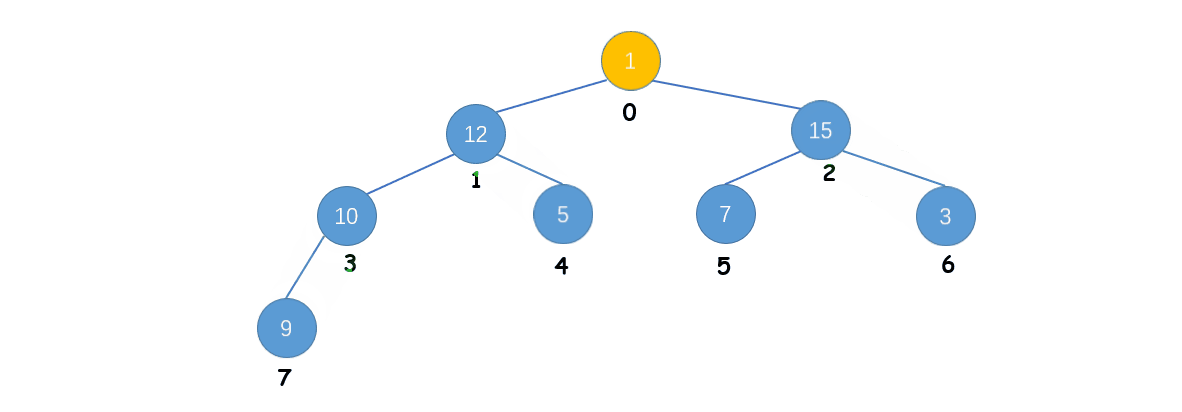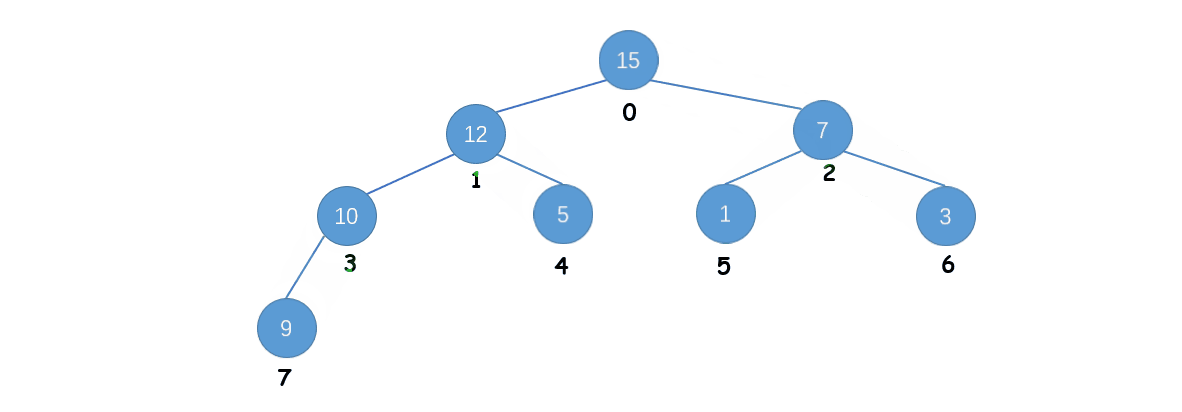
算法思路:
Ⅰ. 构建一个普通的二叉堆
Ⅱ. 找到二叉堆中的第一个非叶子结点
Ⅲ. 从第一个非叶子结点按照逆层序遍历的顺序,对每一个结点进行下沉操作
private void heapify(E[] arr) {
data = new ArrayList<>();
for(E a:arr) {
data.add(a);
}
int noLeaf = parent(data.size()-1);
for(int i = noLeaf; i >= 0; i--) {
siftDown(i);
}
}
时间复杂度分析: heapify 操作的时间复杂度为 O(n)
利用 Comparator 实现一个最小堆
MaxHeap类传入的类型都是可比较的,假如传入的类型是包装类,这些类都继承了 Comparable 接口并实现 CompareTo 方法,也就是已经定义好了规则。这里使用 Comparator 接口 定义一个比较器,就可以更改比较规则,让实际上的大数变成小数
在最大堆中添加一个新的构造方法,并定义一个比较器:
private Comparator<E> comparator;
public MaxHeap(Comparator<E> comparator) {
this.comparator = comparator;
data = new ArrayList<>();
}
将最大堆中所有使用 compareTo 方法进行比较的更新为使用比较器的 compare 方法。
优先队列的基础知识
优先队列仍然是一个队列,具有先进先出的特点;不同之处,优先队列中的元素优先级高的越靠近队头,优先级可以规定值越大优先级越高,相应地就是用最大堆实现优先队列。实现优先队列只需要实现队列中的这些接口:
public interface Queue<E> {
int getSize();
boolean isEmpty();
void enqueue(E element);
E dequeue();
E getFront();
}
全部实现代码
最大堆
import java.util.ArrayList;
public class MaxHeap <E extends Comparable<E>>{
private ArrayList<E> data;
public MaxHeap() {
data = new ArrayList<>();
}
public MaxHeap(E[] arr) {
heapify(arr);
}
public MaxHeap(int Capacity) {
data = new ArrayList<>(Capacity);
}
public int getSize() {
return data.size();
}
public boolean isEmpty() {
return data.isEmpty();
}
//获得双亲结点的索引值
private int parent(int idx) {
return (idx - 1) / 2;
}
//获得左孩子的索引值
private int leftChild(int idx) {
return idx * 2 + 1;
}
//获得右孩子的索引值
private int rightChild(int idx) {
return idx * 2 + 2;
}
public void add(E e) {
if(data.contains(e))
return;
data.add(e);
siftUp(getSize() - 1);
}
private void siftUp(int idx) {
while(idx > 0 && data.get(parent(idx)).compareTo(data.get(idx)) < 0) {
swap(idx, parent(idx));
idx = parent(idx);
}
}
private void swap(int idx1, int idx2) {
E t = data.get(idx1);
data.set(idx1, data.get(idx2));
data.set(idx2, t);
}
public E findMax() {
if(data.size() == 0) {
throw new IllegalArgumentException("No Nodes!");
}
return data.get(0);
}
public E deleteMax() {
E ret = findMax();
swap(0,data.size()-1);
data.remove(data.size()-1);
siftDown(0);
return ret;
}
private void siftDown(int idx) {
while(leftChild(idx) < data.size()) {
int max = leftChild(idx);
if(leftChild(idx)+1 < data.size() && data.get(leftChild(idx)).compareTo(data.get(rightChild(idx))) < 0) {
max = rightChild(idx);
}
if(data.get(idx).compareTo(data.get(max)) < 0) {
swap(idx, max);
idx = max;
}else {
break;
}
}
}
public E replace(E e) {
E ret = data.get(0);
data.set(0, e);
siftDown(0);
return ret;
}
private void heapify(E[] arr) {
data = new ArrayList<>();
for(E a:arr) {
data.add(a);
}
int noLeaf = parent(data.size()-1);
for(int i = noLeaf; i >= 0; i--) {
siftDown(i);
}
}
public String toString() {
StringBuilder str = new StringBuilder();
str.append('[');
for(int i = 0; i < data.size(); i++) {
str.append(data.get(i));
if(i != data.size() - 1)
str.append(',');
}
str.append(']');
return str.toString();
}
}
最小堆
import java.util.ArrayList;
import java.util.Comparator;
public class MaxHeap <E extends Comparable<E>>{
private ArrayList<E> data;
private Comparator<E> comparator;
public MaxHeap() {
data = new ArrayList<>();
}
public MaxHeap(E[] arr) {
heapify(arr);
}
public MaxHeap(Comparator<E> comparator) {
this.comparator = comparator;
data = new ArrayList<>();
}
public MaxHeap(int Capacity) {
data = new ArrayList<>(Capacity);
}
public int getSize() {
return data.size();
}
public boolean isEmpty() {
return data.isEmpty();
}
//获得双亲结点的索引值
private int parent(int idx) {
return (idx - 1) / 2;
}
//获得左孩子的索引值
private int leftChild(int idx) {
return idx * 2 + 1;
}
//获得右孩子的索引值
private int rightChild(int idx) {
return idx * 2 + 2;
}
public void add(E e) {
if(data.contains(e))
return;
data.add(e);
siftUp(getSize() - 1);
}
private void siftUp(int idx) {
while(idx > 0 && comparator.compare(data.get(parent(idx)), data.get(idx)) < 0) {
swap(idx, parent(idx));
idx = parent(idx);
}
}
private void swap(int idx1, int idx2) {
E t = data.get(idx1);
data.set(idx1, data.get(idx2));
data.set(idx2, t);
}
public E findMax() {
if(data.size() == 0) {
throw new IllegalArgumentException("No Nodes!");
}
return data.get(0);
}
public E deleteMax() {
E ret = findMax();
swap(0,data.size()-1);
data.remove(data.size()-1);
siftDown(0);
return ret;
}
private void siftDown(int idx) {
while(leftChild(idx) < data.size()) {
int max = leftChild(idx);
if(leftChild(idx)+1 < data.size() && comparator.compare(data.get(leftChild(idx)), data.get(rightChild(idx))) < 0) {
max = rightChild(idx);
}
if(comparator.compare(data.get(idx), data.get(max)) < 0) {
swap(idx, max);
idx = max;
}else {
break;
}
}
}
public E replace(E e) {
E ret = data.get(0);
data.set(0, e);
siftDown(0);
return ret;
}
private void heapify(E[] arr) {
data = new ArrayList<>();
for(E a:arr) {
data.add(a);
}
int noLeaf = parent(data.size()-1);
for(int i = noLeaf; i >= 0; i--) {
siftDown(i);
}
}
public String toString() {
StringBuilder str = new StringBuilder();
str.append('[');
for(int i = 0; i < data.size(); i++) {
str.append(data.get(i));
if(i != data.size() - 1)
str.append(',');
}
str.append(']');
return str.toString();
}
}
优先队列
public class PriorityQueue <E extends Comparable<E>> implements Queue<E>{
private MaxHeap<E> maxHeap;
public PriorityQueue() {
maxHeap = new MaxHeap<>();
}
@Override
public int getSize() {
return maxHeap.getSize();
}
@Override
public boolean isEmpty() {
return maxHeap.isEmpty();
}
@Override
public void enqueue(E element) {
maxHeap.add(element);
}
@Override
public E dequeue() {
return maxHeap.deleteMax();
}
@Override
public E getFront() {
return maxHeap.findMax();
}
}