通信原理（第七版）常见公式

通信原理（第七版）知识点复习
（1）《通信原理》期末总结——Sunnycee’s Blog
https://sunnycee.cn/archives/2e834616.html
（2）通信原理复习——Pang-Blog
https://pangyuworld.github.io/2019/12/19/%E9%80%9A%E4%BF%A1%E5%8E%9F%E7%90%86%E5%A4%8D%E4%B9%A0/

常用公式总结

第 1 章 绪论

1.4 信息及其度量

1.4.1 离散信源

$I:消息中所含信息量，(b)$
$M:进制$
$P(x):消息出现的概率$
$H(x):平均信息量（熵），(b/符号)$

$$I={\log }_a\frac{1}{P(x)}=-{\log }_{a}P(x)(b)$$

$(1)等概率$
$$I={\log }_2\frac{1}{P}={\log }_2\frac{1}{1/M}={\log }_{2}M(b)$$

$(2)非等概率$
$$H(x)=-\sum _{i=1}^{M}P(x_i){\log }_{2}P(x_i)(b/符号)$$

1.4.2 连续信源

$f(x):连续消息出现的概率密度$

$$H(x)=-{\int }_{-\infty }^{+\infty }f(x){\log }_{a}f(x)dx(b/符号)$$

1.5 通信原理主要性能指标

1.5.1 有效性

$M:进制$
$B:频带带宽，(Hz)$
$\eta :频带利用率，(Baud/Hz)$
${\eta }_b:M进制频带利用率，(b/(s\cdot Hz)$
$R_B:单位时间传输码元的数目，码元传输速率，波特率，(Baud)$
$R_b:单位时间传输平均信息量，信息传输速率，比特率，(b/s)$
$T_B:每个码元的长度，(s)$
$T_b:每个二进制码元的持续时间，(s)$

$$\eta =\frac{R_B}{B}(Baud/Hz)$$

$${\eta }_b=\frac{R_b}{B}(b/(s\cdot Hz))$$

$$R_B=\frac{1}{T_B}(Baud)$$

$$R_b=R_B{\log }_{2}M(b/s)$$

$$T_B=T_b\cdot {\log }_{2}M$$

1.5.2 可靠性

$P_e:误码率$
$P_b:误信率$

$$P_e=\frac{错误码元数}{传输总码元数}$$

$$P_b=\frac{错误比特数}{传输总比特数}$$

第 4 章 信道

4.1 无线信道

	频率	特性	距离	用途
地波	<2MHz	有绕射能力	数百或数千米	AM广播
天波	2~30MHz	被电离层反射	< 4000 km（一跳）	远程、短波通信
视线	>30MHz	直线传播、穿透电离层	与天线高度有关	卫星和外太空通信超短波及微波通信

$h:收发天线的高度，(m)$
$r:地球的等效半径，(km)$
$D:收发天线的距离，(km)$

$$h=\frac{D^2}{8r}\approx \frac{D^2}{50}(m)$$

4.2 编码信道模型

$P(x/y):发送y接收x的概率$

4.4 信道特性对信号传输的影响

${\tau }_m:多径中最大的相对时延差，(s)$
$\Delta f:信道相关带宽，(Hz)$
$B_s:信号带宽，(Hz)$

$$\Delta f=\frac{1}{{\tau }_m}(Hz)$$

$$R_B=B_s=(1/3\sim 1/5)\Delta f(Hz)$$

4.6 信道容量

4.6.1 离散信道容量

$C:每个符号能够传输的平均信息量的最大值，(b/符号)$
$C_t:单位时间内能传输的平均信息量最大值，(b/s)$
$P(x_i):接收端接收x_i（包括正确和错误）$
$P(x_i/y_j):发送端发送y_j，接收端接收x_i$
$r:单位时间内信道传输的符号数，(符号/s)$
$R:信道每秒传输的平均信息量，(b/s)$

$$\begin{array}{rl}平均信息量/符号& =-\sum _{i=1}^{n}P(x_i){\log }_{2}P(x_i)-\left[-\sum _{j=1}^{m}P(y_j)\sum _{i=1}^{n}P(x_i/y_j){\log }_{2}P(x_i/y_j)\right]\\ & =H(x)-H(x/y)\end{array}$$

$$\begin{array}{rl}C& =\underset{P(x)}{\max }\left[H(x)-H(x/y)\right]\\ R& =r\left[H(x)-H(x/y)\right]\\ C_t& =\underset{P(x)}{\max }\{r\left[H(x)-H(x/y)\right]\}\end{array}$$

4.6.2 连续信道容量

$B:频带带宽，(Hz)$
$S:信号平均功率，(W)$
$N:噪声功率，(W)$
$n_0:噪声单边功率谱密度，(W/Hz)$

$$C_t=B{\log }_2\left(1+\frac{S}{N}\right)(b/s)$$

$$C_t=B{\log }_2\left(1+\frac{S}{n_{0}B}\right)(b/s)$$

$$\underset{B\to \infty }{\lim }{C}_t\approx 1.44\frac{S}{n_0}$$

第 5 章 模拟调制系统

5.1 幅度调制（线性调制）原理

$A:载波振幅$
$\omega :载波角频率$
${\phi }_0:载波初始相位$

$$\begin{array}{rl}c(t)& =A\cos ({\omega }_{c}t+\phi )\\ c(t)& =A\cos ({\omega }_{c}t)({\phi }_0=0)\end{array}$$

$$\begin{array}{rl}{\cos }^2\theta & =\frac{1}{2}(1+\cos 2\theta )\\ \sin 2\theta & =2\sin \theta \cos \theta \end{array}$$

5.1.1 调幅调制 AM（Amplitude Modulation）

$$\begin{array}{rl}{S}_{AM}(t)& =\left[A_0+m(t)\cos {\omega }_{c}t\right]\\ & =A_0\cos {\omega }_{c}t+m(t)\cos {\omega }_{c}t\end{array}$$

$$S_{AM}(\omega )=\pi A_0\left[\delta (\omega +{\omega }_c)+\delta (\omega -{\omega }_c)\right]+\frac{1}{2}\left[M(\omega +{\omega }_c)+M(\omega -{\omega }_c)\right]$$

$${\left|m(t)\right|}_{max}\le A_0(防止过调幅)$$

$f_H:基带信号带宽，(Hz)$
$B_{AM}:AM调制信号带宽，(Hz)$
$P_{AM}:AM信号在1\Omega 电阻上的平均功率$
$P_c:载波功率$
$P_s:边带功率$
$m:调幅系数$
${\eta }_{AM}:调制效率$

$$\begin{array}{rl}{P}_{AM}& =\overline{s_{AM}^2(t)}=\overline{[A_0+m(t){]}^2{\cos }^2{\omega }_{c}t}\\ & =\overline{A_0^2{\cos }^2{\omega }_{c}t}+\overline{m^2(t){\cos }^2{\omega }_{c}t}+\overline{2A_{0}m(t){\cos }^2{\omega }_{c}t}\\ & =\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}(\overline{m(t)}=0)\\ & =P_c+P_s\end{array}$$

$$\begin{array}{rl}{P}_c& =\frac{A_0^2}{2}\\ P_s& =\frac{\overline{m^2(t)}}{2}\end{array}$$

$$\begin{array}{rl}{\eta }_{AM}& =\frac{P_s}{P_{AM}}=\frac{\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}\\ & =\frac{1}{2}(|m(t){|}_{max}\le A_0)\\ & =\frac{1}{3}(单音正弦:m(t)=A_m\cos {\omega }_{m}t)\end{array}$$

$$m=\frac{|m(t){|}_{max}}{A_0}$$

$$B_{AM}=2f_H$$

5.1.2 抑制载波双边带调制 DSB-SC（Double-Side-Band Suppressed Carrier）

$$S_{DSB}(t)=m(t)\cos {\omega }_{c}t(抑制载波)$$

$$S_{DSB}(\omega )=\frac{1}{2}\left[M(\omega +{\omega }_c)+M(\omega -{\omega }_c)\right]$$

$$B_{DSB}=B_{AM}=2f_H$$

$$\eta =100\%$$

5.1.3 单边带调制 SSB（Single-Side-Band）

(1) 滤波法
$H(\omega ):传输函数$

$$\begin{array}{rl}H(\omega )& =H_{USB}(\omega )=\{\begin{array}{r}1|\omega |>{\omega }_c\\ 0|\omega |\le {\omega }_c\end{array}\\ H(\omega )& =H_{LSB}(\omega )=\{\begin{array}{r}1|\omega |<{\omega }_c\\ 0|\omega |\ge {\omega }_c\end{array}\\ S_{SSB}& =S_{DSB}(\omega )\cdot H(\omega )\end{array}$$

(2) 相移法

$$\begin{array}{rl}m(t)& =A_m\cos {\omega }_{m}t\\ c(t)& =\cos {\omega }_{c}t\\ A_m\sin {\omega }_{m}t& =A_m\hat{\cos }{\omega }_{m}t(希尔伯特变换)\\ S_{SSB}& =m(t)\cdot c(t)\\ & =\frac{1}{2}m(t)\cos {\omega }_{c}t\mp \frac{1}{2}\widehat{m(t)}\sin {\omega }_{c}t\end{array}$$

$$B_{SSB}=\frac{B_{DSB}}{2}=f_H$$

5.1.4 残留单边带调制 VSB（Vestigial-Side-Band）

${\omega }_H:调制信号截止频率$

$$H(\omega +{\omega }_c)+H(\omega -{\omega }_c)=常数|\omega |\le {\omega }_H$$

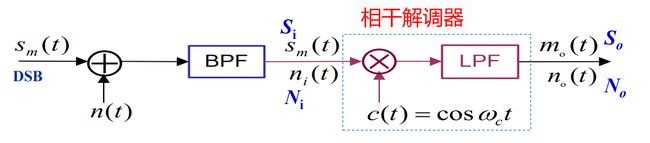
5.2 线性调制系统的抗噪性能

$n_i(t):平稳窄带高斯噪声$
$n_c(t):窄带噪声同向分量$
$n_s(t):窄带噪声正交分量$
$S_i:输入已调信号的平均功率$
$N_i:输入噪声的平均功率$
$S_o:输出有用信号的平均功率$
$N_o:输入噪声的平均功率$
$G:调制制度增益（信噪比增益）$

$$\begin{array}{rl}{n}_i(t)& =n_c\cos {\omega }_{0}t-n_s\sin {\omega }_{0}t\\ \overline{n_i^2(t)}& =\overline{n_c^2(t)}=\overline{n_s^2(t)}=N_i\\ N_i& =n_{o}B(单边谱密度n_o，带通滤波器高度1，带宽B)\end{array}$$

$$\begin{array}{rl}\frac{S_i}{N_i}& =\frac{\overline{s_m^2(t)}}{\overline{n_i^2(t)}}\\ \frac{S_o}{N_o}& =\frac{\overline{m_o^2(t)}}{\overline{n_o^2(t)}}\\ G& =\frac{S_o/N_o}{S_i/N_i}\end{array}$$

重要三角变换公式
$$\begin{array}{rl}{\cos }^2\theta & =\frac{1}{2}(1+\cos 2\theta )\\ \sin 2\theta & =2\sin \theta \cos \theta \end{array}$$

5.2.2 DSB调制系统性能（抑制正交分量）

$$\begin{array}{rl}{s}_m(t)& =m(t)\cos {\omega }_{c}t\\ m_o(t)& =s_m(t)\cos {\omega }_{c}t=m(t)\cos {\omega }_{c}t\cos {\omega }_{c}t\\ n_o(t)& =n_i\cos {\omega }_{c}t\end{array}$$

$$\begin{array}{rl}{S}_i& =\overline{s_m^2(t)}=\frac{1}{2}\overline{m^2(t)}\\ N_i& =\overline{n_i^2}=n_{0}B\\ S_o& =\overline{m_o^2(t)}=\frac{1}{4}\overline{m^2(t)}\\ N_o& =\overline{n_o^2}=\frac{1}{4}{N}_i\\ G_{DSB}& =\frac{S_o/N_o}{S_i/N_i}=2\end{array}$$

5.2.3 SSB调制系统性能（抑制正交分量）

$$\begin{array}{rl}{s}_m(t)& =\frac{1}{2}m(t)\cos {\omega }_{c}t\mp \frac{1}{2}\widehat{m(t)}\sin {\omega }_{c}t\\ m_o(t)& =s_m(t)\cos {\omega }_{c}t\\ n_o(t)& =n_i\cos {\omega }_{c}t\end{array}$$

$$\begin{array}{rl}{S}_i& =\overline{s_m^2(t)}=\frac{1}{4}\overline{m^2(t)}\\ N_i& =\overline{n_i^2}=n_{0}B\\ S_o& =\overline{m_o^2(t)}=\frac{1}{16}\overline{m^2(t)}\\ N_o& =\overline{n_o^2}=\frac{1}{4}{N}_i\\ G_{SSB}& =\frac{S_o/N_o}{S_i/N_i}=1\end{array}$$

5.2.4 AM 包络波的性能

$$\begin{array}{rl}{s}_m(t)& =\left[A_0+m(t)\right]\cos {\omega }_{c}t\\ S_i& =\overline{s_m^2(t)}=\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}\\ N_i& =\overline{n_i^2}=n_{0}B\end{array}$$

$$\begin{array}{rl}{s}_m(t)+n_i(t)& =E(t)\cos \left[{\omega }_{c}t+\psi (t)\right]\\ E(t)& =\sqrt{{\left[A_0+m(t)+n_c(t)\right]}^2+n_s^2(t)}\\ \psi & =\arctan \left[\frac{n_s(t)}{A_0+m(t)+n_c(t)}\right]\end{array}$$

(1) 大信噪比情况

$$\begin{array}{rl}{S}_o& =\overline{m^2(t)}\\ N_o& =\overline{n_c^2(t)}=\overline{n_i^2(t)}=n_{0}B\\ G_{AM}& =\frac{S_o/N_o}{S_i/N_i}=\frac{2\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}\\ & =\frac{2}{3}(单频正弦)\end{array}$$

(2) 小信噪比情况（门限效应）

5.3 非线性调制（角度调制）原理

$PM:相位调制$
$FM:频率调制$
$\phi (t):相对于载波相位{\omega }_c(t)的瞬时相位偏移$

$$\begin{array}{rl}{s}_m(t)& =A\cos [{\omega }_{c}t+\phi (t)]\\ \phi (t)& =K_{p}m(t)\\ s_{PM}(t)& =A\cos [{\omega }_{c}t+K_{p}m(t)]\\ \frac{d\phi (t)}{dt}& =K_{f}m(t)\\ s_{FM}(t)& =A\cos [{\omega }_{c}t+K_f\int m(\tau )d\tau ]\end{array}$$

$m_p:调相指数，最大的相位偏移$
$m_f:调频指数，最大的相位偏移$
$\Delta \omega :最大角频偏$
$\Delta f:最大频偏$

$$\begin{array}{rl}{m}_t& =A_m\cos {\omega }_{m}t=A_m\cos 2\pi f_{m}t\\ s_{PM}t& =A\cos [{\omega }_{c}t+K_p{A}_m\cos {\omega }_{m}t]\\ & =A\cos [{\omega }_{c}t+m_p\cos {\omega }_{m}t]\\ m_p& =K_p{A}_m\\ s_{FM}t& =A\cos \left[{\omega }_{c}t+K_f{A}_m\int \cos {\omega }_m\tau d\tau \right]\\ & =A\cos [{\omega }_{c}t+m_f\sin {\omega }_{m}t]\\ m_f& =\frac{K_f{A}_m}{{\omega }_m}=\frac{\Delta \omega }{{\omega }_m}=\frac{\Delta f}{f_m}\end{array}$$

5.3.2 窄带调频/宽带调频

(1) 基本信息

$$\{\begin{array}{rlr}& K_f\int m(\tau )d\tau \ll \frac{\pi }{6}or0.5& (NBFM)\\ & 不满足上述条件& (WBFM)\end{array}$$

$$\begin{array}{rl}{B}_{FM}& =2(m_f+1)f_m=2(\Delta f+f_m)\\ & \approx 2f_m(m_f\ll 1NBFM)\\ & \approx 2\Delta f(m_f\gg 1WBFM)\end{array}$$

(2) 阿姆斯特朗法

$$\begin{array}{rl}{f}_c& =n_2(n_1{f}_1-f_2)\\ \Delta f& =n_1{n}_2\Delta f_1\end{array}$$

5.4 调频系统抗噪性能分析

$$G_{FM}=\frac{3}{2}{m}_f^2\left(\frac{B_{FM}}{f_m}\right)$$

5.5 各种模拟调制的比较

调制方式	传输带宽	输出信噪比	制度增益	设备复杂程度
AM	$2f_m$	${\left(\frac{S_o}{N_o}\right)}_{AM}=\frac{1}{3}\left(\frac{S_i}{n_0{f}_m}\right)$	2/3	简单
DSB	$2f_m$	${\left(\frac{S_o}{N_o}\right)}_{DSB}=\left(\frac{S_i}{n_0{f}_m}\right)$	2	中等
SSB	$f_m$	${\left(\frac{S_o}{N_o}\right)}_{SSB}=\left(\frac{S_i}{n_0{f}_m}\right)$	1	复杂
VSB	$>\approx f_m$	$\approx SSB$	$\approx SSB$	复杂
FM	$2(m_f+1)f_m$	${\left(\frac{S_o}{N_o}\right)}_{FM}=\frac{3}{2}{m}_f^2\left(\frac{S_i}{n_0{f}_m}\right)$	$3m_f^2(m_f+1)$	中等

第 6 章 数字基带传输系统

6.1.1 数字基带信号

(a) 单极性波形
$1\to +E$
$0\to 0$

(b) 双极性波形
$1\to +E$
$0\to -E$

© 单极性归零波形（RZ）
$1\to +E$（提前归零，占空比一般 50%）
$0\to 0$

(d) 双极性归零波形（RZ）
$1\to +E$（提前归零，占空比一般 50%）
$0\to -E$（提前归零，占空比一般 50%）

(e) 差分波形
有跳表示“1”，无跳表示“0”

(f) 多电平波形

6.2.2 常用传输码型

(1) AMI 码
$0\to 0$
$1\to -1/+1（交替出现，一般从-1开始）$

(2) $HD{B}_3码$
$0\to 0$
$1\to -1/+1（交替出现，一般从-1开始）$
$[1]满足前一个相邻的非“0”脉冲极性相同，且满足前一个相邻的“V”码极性交替：0000\to 000\mp V（相邻“V”码之间有奇数个1）$
$[2]否则：0000\to \mp B00\mp V（相邻“V”码之间有偶数个1）$

(3) 双相码（双极性NRZ波形）
$1\to 10$
$0\to 01$

(4) 差分双相码
有跳表示“1”，无跳表示“0”

(5) CMI 码
$1\to 11/00（交替出现）$
$0\to 01$

(6) 块编码

6.3 数字基带传输与码间串扰

$G_T(\omega ):发送滤波器的传输特性$
$C(\omega ):信道的传输特性$
$G_R(\omega ):接受滤波器的传输特性$
$H(\omega ):基带传输系统的总传输特性$

$$H(\omega )=G_T(\omega )C(\omega )G_R(\omega )$$

6.4 无码间串扰的基带传输特性

6.4.3 无码间串扰传输特性设计

(1) 理想低通特性
实现抽样时，仅仅只有基带系统有值，而其他系统刚好处于零点，实现无码间串扰

$f_N:奈奎斯特带宽$

$$\begin{array}{rl}{f}_N& =B=\frac{1}{2T_B}(Hz)\\ R_B& =\frac{1}{T_B}=2f_N(Baud)\\ \eta & =\frac{R_B}{B}=2(Baud/Hz)\end{array}$$

(2) 余弦滚降特性
理想低通特性以奈奎斯特带宽$f_N$为中心，按奇对称条件进行余弦滚降

$\alpha :余弦滚降系数$

$$\begin{array}{rl}\alpha & =\frac{f_{\Delta }}{f_N}\\ R_B& =2f_N\\ B& =f_{\Delta }+f_N=(1+\alpha )f_N\\ \eta & =\frac{R_B}{B}=\frac{2}{1+\alpha }(Baun/Hz)\end{array}$$

第 7 章 数字带通传输系统

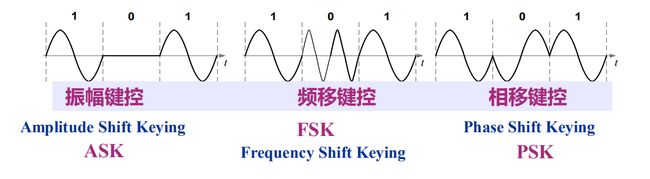
7.1 二进制数字调制原理

7.1.1 二进制振幅键控（2ASK）

$$e_{2ASK}=\{\begin{array}{rlrl}& A\cos {\omega }_{c}t& 1& (P)\\ & 0& 0& (1-P)\end{array}$$

7.1.2 二进制频移键控（2FSK）

$$e_{2FSK}=\{\begin{array}{rlr}& A\cos ({\omega }_{1}t+{\phi }_n)& 1\\ & A\cos ({\omega }_{2}t+{\theta }_n)& 0\end{array}$$

7.1.3 二进制相移键控（2PSK）

$$e_{2PSK}=\{\begin{array}{rlr}& A\cos {\omega }_{c}t& 1\\ & -A\cos {\omega }_{c}t& 0\end{array}$$

7.1.4 二进制差分相移键控（2DPSK）
计算出相对码，推算得到相位差，后面图形在前面图形移动对应相位

$a_n:绝对码$
$b_n:相对码$

$$b_n=a_n⨁b_{n-1}$$

$$\begin{array}{rl}{e}_{2DPSK}& =A\cos ({\omega }_{c}t+\Delta \phi )\\ \Delta \phi & =\{\begin{array}{rlr}& \pi & 1\\ & 0& 0\end{array}\end{array}$$

7.3 二进制数字调制系统的性能比较

7.3.1 误码率

	相干解调	非相干解调
2ASK	$\frac{1}{2}erfc\left(\sqrt{\frac{r}{4}}\right)$	$\frac{1}{2}{e}^{-r/4}$
2FSK	$\frac{1}{2}erfc\left(\sqrt{\frac{r}{2}}\right)$	$\frac{1}{2}{e}^{-r/2}$
2PSK	$\frac{1}{2}erfc\left(\sqrt{r}\right)$
2DPSK	$erfc\left(\sqrt{r}\right)$	$\frac{1}{2}{e}^{-r}$

7.3.2 带宽与频带利用率

$当信号带宽为T_B$

	$带宽B$
2ASK	$2R_B=\frac{2}{T_B}$
2FSK	$\mid f_2-f_1\mid +2R_B$
2PSK	$2R_B=\frac{2}{T_B}$
2DPSK	$2R_B=\frac{2}{T_B}$