图及其应用c语言实现(数据结构复习最全笔记)(期末复习最新版)
图
一.图的基本概念
1.图的定义
图是由顶点(vertex)集合及顶点间的关系组成的一种数据结构。Graph=(V,E)Graph=(V,E)其中,顶点集合 V={x|x∈某个对象数据集}V={x|x∈某个对象数据集} 是有穷非空集合;E={(x,y)|x,y∈V}E={(x,y)|x,y∈V} 是顶点间关系的有穷集合,也叫边(edge)集合。Path(x,y)Path(x,y)表示从顶点x到y的一条单向通路,他是有方向的。
2.图的相关概念
∙∙ 有向图(Directed Graph):一般用
∙∙ 无向图(Undirected Graph):一般用(u,v)(u,v)表示
∙∙ 完全图(Complete Graph):在n个顶点组成的无向图中,若有n(n−1)2n(n−1)2条边,则称为无向完全图。在n个顶点组成的有向图中,若有n(n−1)n(n−1)条边,则称为有向完全图。完全图中的边数达到最大。
..稀疏图:边或弧很少的图
..稠密图:边或弧很多的图
∙∙ 权(Weight):在某些图中,边具有与之相关的数量(比如一个顶点到另一个顶点的距离、花费的代价、所需的时间、次数等)。这种带权图也叫做网络(Network)。
∙∙ 邻接顶点(Adjacent vertex):如果(u,v)是E(G)中的一条边,则u和v互为邻接顶点,且边(u,v)依附于顶点u和v,顶点u和v依附于边(u,v)。如果
∙∙ 子图(Subgraph):Subgraph Let G = (V, E) be a graph with vertex set V and edge set E. A subgraph of G is a graph G’ = (V’, E’) where
1. V’ is a subset of V
2. E’ consists of edges (v, w) in E such that both v and w are in V’
∙∙ 度(Degree):与顶点v关联的边数,称为v的度,记作deg(v)。有向图中,顶点的度是入度和出度之和。顶点v的入度是指以v为终点的有向边的条数,记作indeg(v),顶点v的出度是指以v为始点的有向边的条数,记作outdeg(v)。顶点v的度为deg(v)=indeg(v)+outdeg(v)。一般地,若图中有n个顶点,e条边,那么:e=12{∑ni=1deg(vi)}e=12{∑i=1ndeg(vi)}
∙∙ 路径(Path)&路径长度(Path length):路径可以用顶点序列表示,在某些算法中,也可用一系列边来表示。对与不带权图,路径长度指的是此路径上边的条数,对于带权图,路径长度指的是此路径上各条边的权值之和。
∙∙ 简单路径&回路(Cycle):路径上各顶点互不重复,这样的路径为简单路径。路径上第一个顶点与最后一个顶点重合,这样的路径为回路。
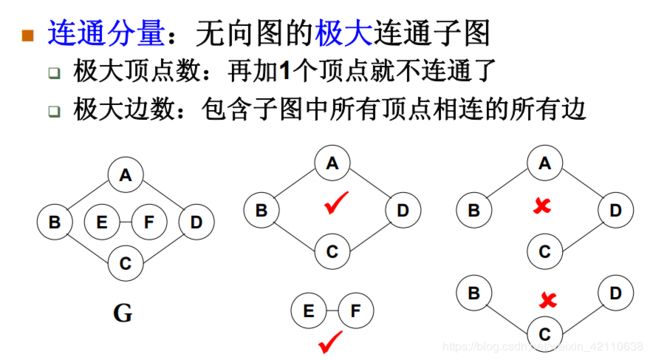
∙∙ 连通图(Connected graph)&连通分量(Connected component ):无向图中,若从顶点v1到顶点v2顶点v1到顶点v2有路径,则称顶点v1与顶点v2顶点v1与顶点v2是连通的。如果图中任一对顶点都是连通的,则称此图是连通图。非连通图的极大连通子图叫做连通分量。
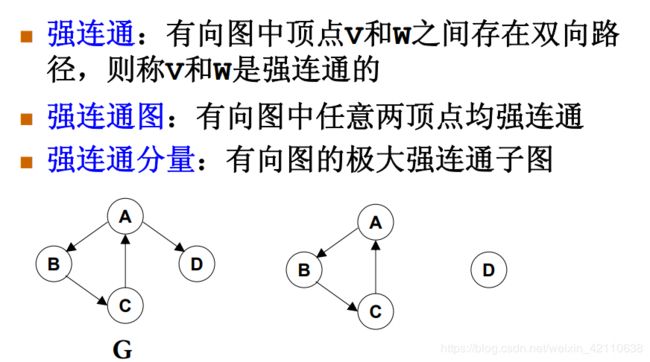
∙∙ 强连通图(Strongly connected graph)&强连通分量(Strongly connected component ):有向图中,若在每一对顶点vi到顶点vj顶点vi到顶点vj之间存在一条从顶点vi到顶点vj顶点vi到顶点vj的路径,也存在一条从顶点vj到顶点vi顶点vj到顶点vi的路径,则称此图是强连通图。非强连通图的极大强连通子图叫做强连通分量。
∙∙ 生成树(Spanning tree):一个无向连通图的生成树是它的极小连通子图,若图中有n个顶点,则其生成树由n-1条边构成。若是有向图,则可能得到它的若干有向树组成的森林。
∙∙ 最小生成树(Minimum spanning tree):一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
*包含图的所有顶点,n-1条边
*没有回路
*边的权重和最小
由此可知,如果一个图有n个顶点和小于n-1条边,则是非连通图。
如果一个图有n个顶点和大于n-1条边,则必定形成环
此外,有n-1条边的不一定事生成树
3.图的相关性质(重点)
a:在无向图中,与一个顶点关联的边数称为该顶点的度,一般使用d表示,设G=(V,E)是一个无向图,令n=|V|,e=|E|,
则每个顶点度数之和等于2e;0<=e<=n(n-1)/2。
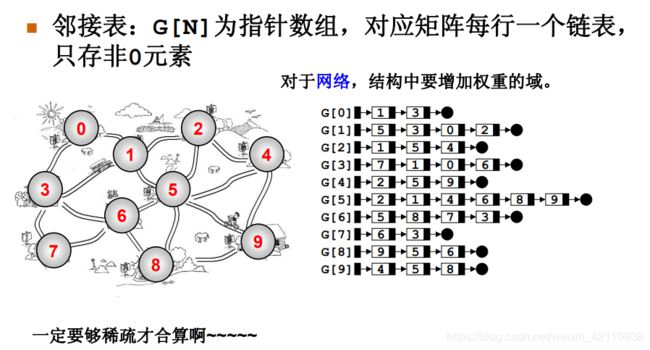
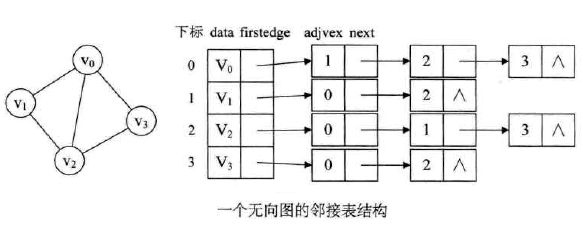
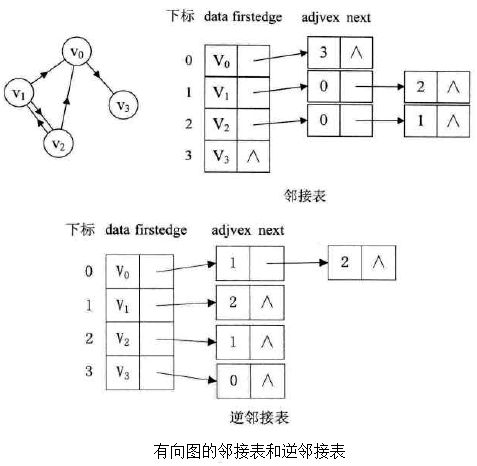
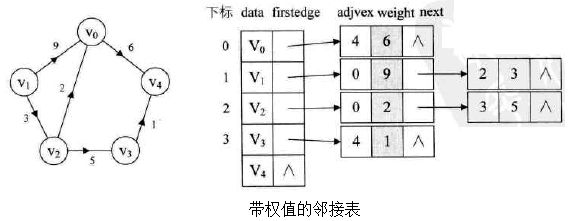
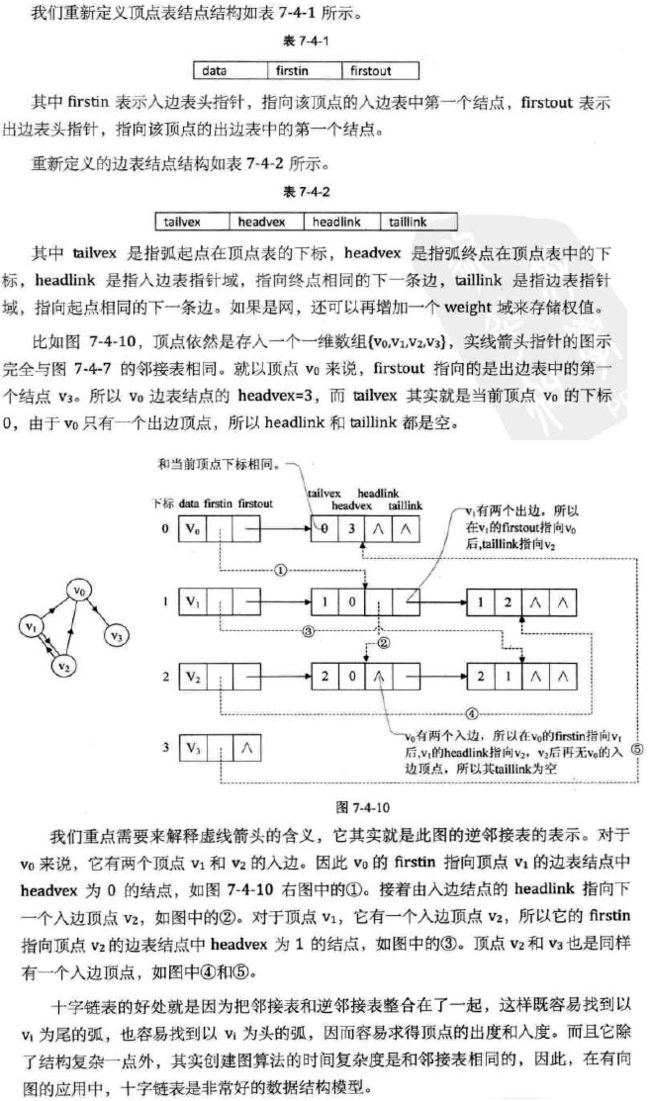
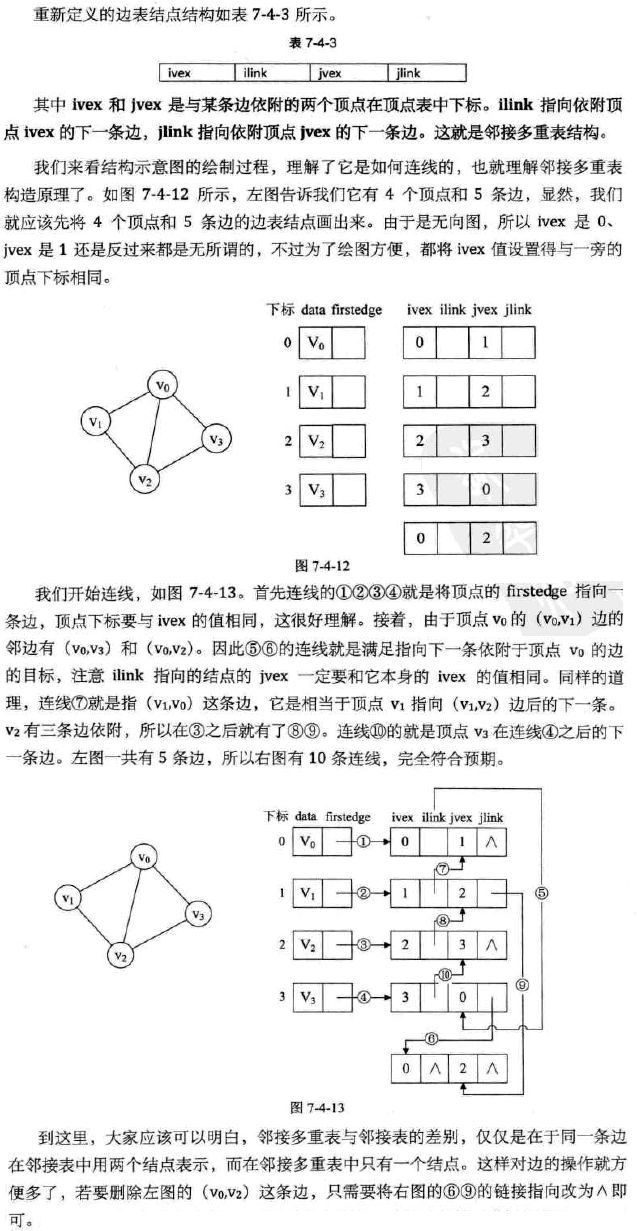
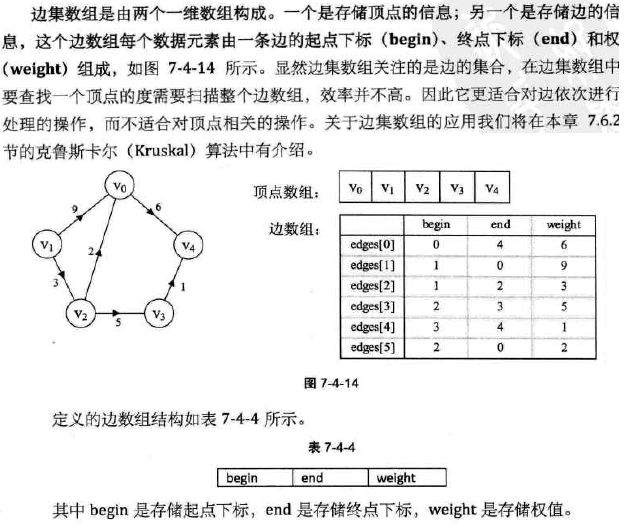
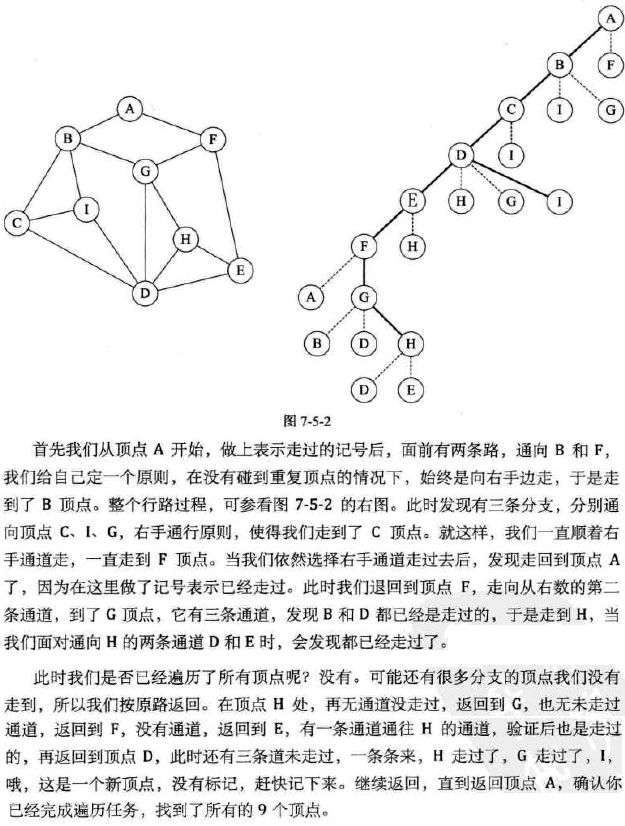
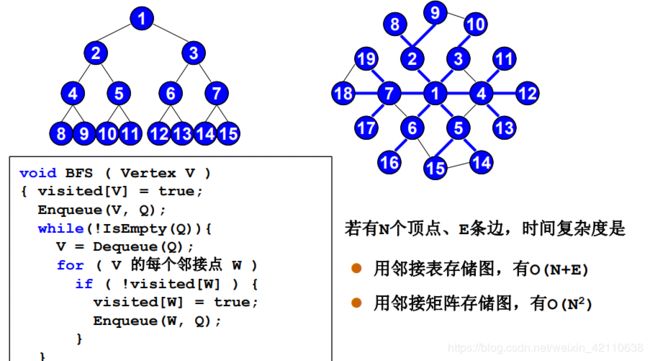
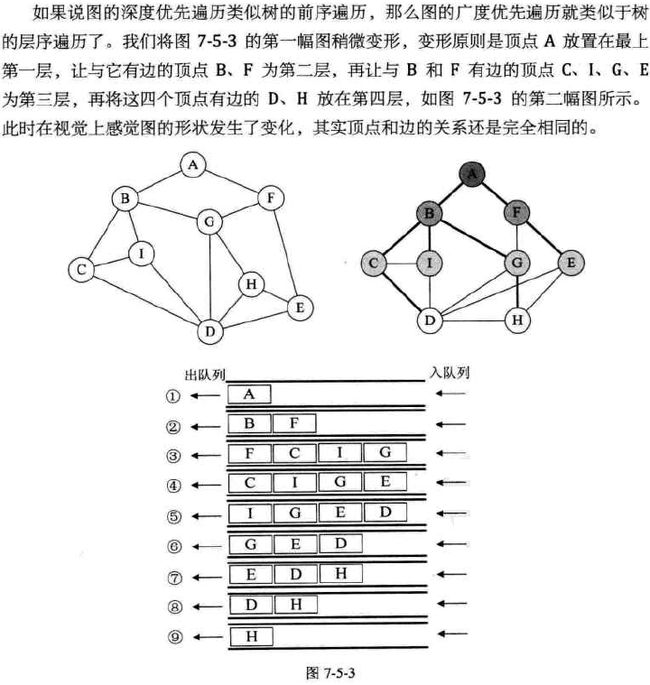
b:在有向图中,一个顶点的入度是指关联至该顶点的边数,顶点的出度是指,关联于该顶点的边数。设G=(V,E)是一个无向图,令n=|V|,e=|E|,则图G的每个节点的出度之和和入度之和相等等于e,0<=e c:具有n个结点的无向完全图共有n*(n-1)/2条边 d:具有n个结点的有向完全图共有n*(n-1)条边 关于图的存储结构,可以分为以下五种(前两种必会): 图的邻接矩阵存储方式是用两个数组来表示图: 一个一维数组存储图中顶点信息; 一个二维数组(称为邻接矩阵)存储图中边或弧的信息 (2) 邻接表 邻接矩阵是一种不错的图存储结构。 但是:对于边树相对顶点较少的图,这种结构是存在存储空间的极大浪费的。 因此我们考虑先进一步,使用邻接表存储,关于邻接表的处理办法是这样: 需要N个头指针 + 2E个结点(每个结点至少2个域),则E小于多少是省空间的?也就是多稀疏才是合算的? 下图是一个无向图的邻接表结构: 对于有向图而言,我们会发现邻接表只适合计算其出度,并不能较好的计算入度。 为了更便于确定顶点的入度(或以顶点为弧头的弧),我们可以建立一个有向图的逆邻接表。 如下图所示: 而对于有权值的网图,可以在边表节点定义中再增加一个weight的数据域,存储权值信息即可。 如下图所示: 那么,有了这些结构的图,下面定义代码如下: (3) 十字链表 对于有向图而言,邻接表也是有缺陷的。 试想想哈,关心了出度问题,想了解入度问题就必须把整个图遍历才能知道。 反之,逆邻接表解决了入度问题却不了解出度的情况。 那是否可以将邻接表和逆邻接表结合起来呢?答案是肯定的。 这就是所谓的存储结构:十字链表。其详解如下图: (4) 邻接多重表 有向图的优化存储结构为十字链表。 对于无向图的邻接表,有没有问题呢?如果我们要删除无向图中的某一条边时? 那也就意味着必须找到这条边的两个边节点并进行操作。其实还是比较麻烦的。比如下图: 欲删除上图中的(V0,V2)这条边,需要对邻接表结构中右边表的阴影两个节点进行删除。 仿照十字链表的方式,对边表节点的结构进行改造如下: (5)边集数组 边集数组侧重于对边依次进行处理的操作,而不适合对顶点相关的操作。 关于边集数组详解如下: 图的遍历图和树的遍历类似,那就是从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这个过程就叫做图的遍历。 对于图的遍历来说,如何避免因回路陷入死循环,就需要科学地设计遍历方案,通过有两种遍历次序方案:深度优先遍历和广度优先遍历。 (1) 深度优先遍历 深度优先遍历(Depth_First_Search),也称为深度优先搜索,简称DFS。 为了更好的理解深度优先遍历。请看下面的图解: 其实根据遍历过程转换为右图后,可以看到其实相当于一棵树的前序遍历。 下面给出遍历算法实现代码 邻接矩阵的dfs算法实现 要注意的是,实际做题时遍历函数的参数有很多种,你得自己会变通 举个简单的例子,dfs也可以这么写(其实本质都一样) 或者 邻接表的dfs算法实现 你也可以这么写 (2)广度优先遍历 广度优先遍历(Breadth_First_Search),又称为广度优先搜索,简称BFS。 深度遍历类似树的前序遍历,广度优先遍历类似于树的层序遍历。 邻接矩阵实现 但在做题时往往需要用数组模拟队列来进行bfs,其邻接表的实现方法如下 邻接表实现 思考 :如果图不连通怎么办 参考这篇博客就成:https://blog.csdn.net/weixin_42110638/article/details/84195985 一下三个较难,至少要学会原理,算法实现尽量学会 同样参考这篇链接就成:https://blog.csdn.net/weixin_42110638/article/details/84223131 同样参考这篇链接就成:https://blog.csdn.net/weixin_42110638/article/details/84350009 同样参考这篇链接就成:https://blog.csdn.net/weixin_42110638/article/details/84246833 二.图的抽象数据类型
三.图的存储结构
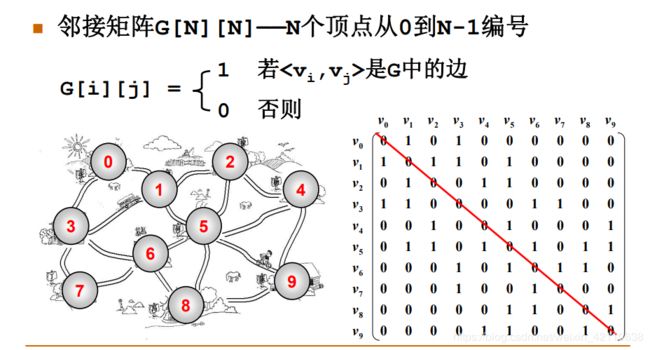
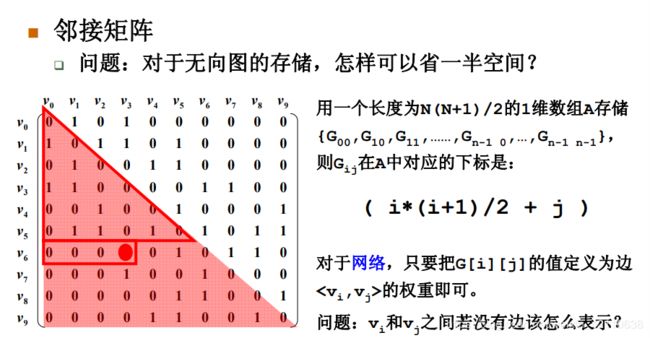
(1) 邻接矩阵
四.图的遍历(最重要的)
void Visit( Vertex V )
{
printf(" %d", V);
}
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) )
{
Vertex j;
Visited[V] = true;//表示从V开始访问
Visit(V);//访问V,其实抛开题来讲这里一般都是打印V
for(j = 0;j < Graph->Nv;j++)
{
if(Graph->G[V][j] == 1 && !Visited[j])//邻接矩阵等于1代表有边,此时如果还没被访问就递归调用
DFS(Graph,j,Visit);
}
}
void DFS(int v)//邻接矩阵的dfs
{
visited[v] = 1;
cout<void DFS(MGraph G, int i){
int j;
printf("%d ", G.vexs[i]);
visited[i] = 1;
for(j = 0; j < G.numV; j++){
if(G.arc[i][j] == 1 && !visited[j]){
DFS(G, j);
}
}
}
void DFSTraverse(MGraph G){
int i;
for(i = 0; i < G.numV; i++){
visited[i] = 0;
}
for(i = 0; i < G.numV; i++){
if(!visited[i]){
DFS(G, i);
}
}
}/* 邻接表存储的图 - DFS */
void Visit( Vertex V )
{
printf(" %d\n", V);
}
/* Visited[]为全局变量,已经初始化为false */
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
PtrToAdjVNode W;
Visit( V ); /* 访问第V个顶点 */
Visited[V] = true; /* 标记V已访问 */
for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( !Visited[W->AdjV] ) /* 若W->AdjV未被访问 */
DFS( Graph, W->AdjV, Visit ); /* 则递归访问之 */
}void DFS(Graph *G, int i)//邻接表的深度优先递归算法
{
EdgeNode *p;
visited[i] = 1;
printf("%d", G->adjList[i].data);
p = G->adjList[i].firstedge;
while(p){
if(!visited[p->adjvex]){
DFS(G, p->adjvex);
}
p = p->next;
}
}
void DFSTraverse(Graph *G)//邻接表的深度遍历操作
{
int i;
for(i = 0; i < G->maxVertexes; i++){
visited[i] = 0;
}
for(i = 0; i < G->maxVertexes; i++){
if(!visited[i]){
DFS(G, i);
}
}
}
/* 邻接矩阵存储的图 - BFS */
/* IsEdge(Graph, V, W)检查void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) )
{
int queue[1010];
int l=0,r=0;//l是队头,r是队尾
queue[r++]=S;//插入到队尾
Visit (S);
Visited[S]=true;
PtrToAdjVNode tmp;//边表结点指向下一个临界点的指针,其实就是next
while(l!=r)//就是队不空
{
tmp=Graph->G[queue[l++]].FirstEdge;//找到当前顶点边表链表头指针,queue[l++]就是每次循环队头都要出队。l++在这里相当于边表遍历完了之后开始遍历下一个顶点表
while(tmp)
{
Vertex pos=tmp->AdjV;//pos为邻接点下标
if(!Visited[pos])//没访问就访问它
{
Visit(pos);
Visited[pos]=true;
queue[r++]=pos;//插入到队尾
}
tmp=tmp->Next;//指针指向下一个邻接点
}
}
}
void BFSTravel(GraphAdjList *g)
{
int i;
int tmp;
EdgeNode *p;
queue q;
for(i=0;i五.图的建立详解
六.最小生成树
七.最短路径
八.拓扑排序与关键序列