利用生成对抗网络保护通信（learning to Protect Communications with Adversarial Neural Cryptography）附代码
这篇博客介绍的知识能够用到我前两篇博客的知识，如果对对抗生成网络GAN和tensorboard可视化不了解的， 请移步，内含代码
- 生成对抗网络GAN---生成mnist手写数字图像示例
- tensorflow的可视化工具tensorboard
密码技术与我们息息相关，使用密码技术不仅仅能够保证信息的机密性，而且可以保证信息的完整性和可用性，防止信息被篡改、伪造和假冒。一直以来，设计和破解密码都是人类的专利，然而，随着人工智能的发展，Google Brain的研究成果《让神经对抗网络学习保护通信》（learning to Protect Communications with Adversarial Neural Cryptography）， 试图让用0和1思考的机器学习对信息进行加密。
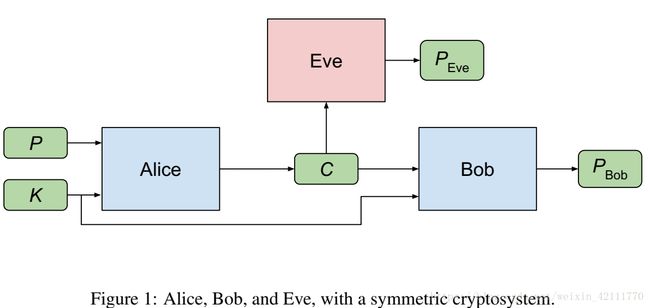
下面简要介绍一下对称加密算法：假设两个人要进行通信，定义为Alice和Bob，很自然，Alice和Bob想要私密的通信，可是有一个破坏者Eve想要窃取Alice和Bob之间的通信信息，所以Alice就把要发送的信息（我们称其为明文P）用秘钥K进行加密得到密文C，然后将密文C发送给Bob，Eve和Bob都能够接触到密文C，由于Bob手中有秘钥K，就可以将密文C恢复成明文P，也就是能够得到Alice发送的信息，然而Eve仅仅能够接触到密文，没有秘钥，所以就不能够得到明文P， 这就是对称加密算法。
对称加密系统
Alice，Bob，Eve三个都是神经网络，它们的参数分别为
, 
和
。我们向神经网络Alice中投入明文P和秘钥K数据，它的计算结果会作为密文C，与秘钥K一起交给另一个神经网络Bob，并优Bob进行解密得到
。Eve接收到密文C， 试图去恢复明文P，得到
。这三个神经网络模块共同构成了对抗神经网络的主体，Alice和Bob组成的网络看做GAN中的生成模型G， 而Eve则被看做GAN中的批判模型D，我们希望Eve恢复秘钥的概率为0.5，在这里是对等于恢复秘钥的位数为明文的1/2，即相当于瞎猜一样。
下面介绍一些网络的细节：
- Alice和Bob有着相同的网络结构，但是输入，输出和参数不同。
- P和K是由-1和1组成的比特串，和是位于区间（-1,1）之间的浮点数，在最后计算准确率的时候，把和中的浮点数转换成整数-1和1，大于等于0的为1，小于0的则为-1。
- 每一个明文对应一个密文
| 网络模型 | 输入 | 输出 |
| Alice | P, K |  |
| Bob | C, K |  |
| Eve | C |  |
损失函数
Eve目标是能够准确地从窃听到的密文C中恢复出明文P，也就是说要尽可能地缩小P和之间误差，选择使用L1范数作为Eve的损失函数，其中d就是指的是P和之间的L1范数值。
Alice和Bob的目标不仅仅使得能够 使得P和之间的误差比较小，而且还要能够安全准确地进行通信，Alice和Bob之间的损失函数为：
网络架构
首先一个全连接层，输入数量等于输出数量，全连接层的输入为明文P和秘钥K，全连接层后面跟着4个1-D的卷积层，每个卷积层的window size，input depth输入深度和output depth输出深度分别为[4, 1, 2], [2, 2, 4], [1, 4, 4]和[1, 4, 1]，步长strides分别为1,2,1,1，这样，最后一层的向量的个数为明文长度。除了最后一个卷积层，其他层（全连接层+3个卷积层）的激活函数为sigmoid函数，最后一个卷积层的激活函数为tanh函数，是因为要使得和的取值位于（-1,1）区间。下图是Alice神经网络的架构，由于Bob和Alice网络架构相似，不同的是Bob的输入为密文C和秘钥K。
由于Eve的输入仅仅只有秘钥K，所以网络架构和Alice和Bob的略微有些差别。需要在全连接层前面再多加上一个N*2N全连接层
结果
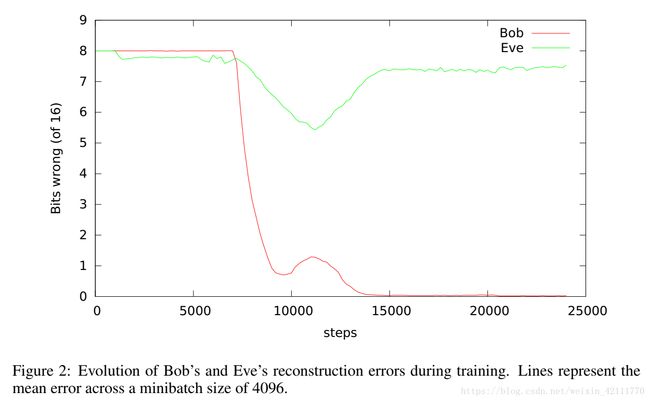
下面的训练结果取自明文和密文的长度都是16, minibatch的大小为4096。理想的结果应当时Bob恢复明文的错误比特数为0，Eve恢复明文的比特数为8。在这个例子中，训练刚开始，Bob和Eve的错误位数都是8， 对于一个16位的二进制文本来说，随便生成的16位数字在概率上错误位数就是8--这时候Bob和Eve都还没有具备解密的能力，伴随的神经网络之间的对抗，每个神经网络不断的调整参数值，Alice和Bob也逐渐获得了极强的加密和解密能力。 当迭代7000次的时候，Bob预测明文的错误率大幅度下滑，在15000次迭代之后，Bob恢复明文的错误率已经几乎为0，而这时Eve的错误位数仍然在8左右波动，也就是说Eve的破解密码的能力基本上等同于瞎猜，所以这时候Alice发出的信息非常安全 。
我的代码实现
gitHub源代码：https://github.com/skloisMary/Adversarial-Neural-Cryptography.git
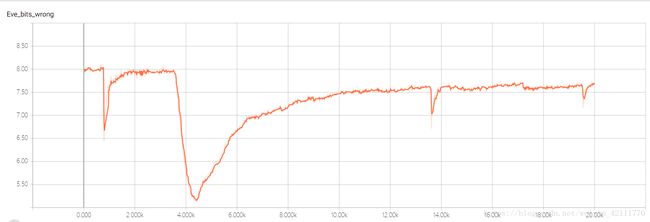
下面的两幅图明文和密文的长度为16，minibatch大小为4096时的结果，在tensorboard中显示，可以看出，Bob几乎能够正确地恢复出明文，Eve恢复明文P的错误位数稳定于7.6bits。
当明文长度取值32比特时，Eve恢复明文时的错误比特数大约稳定于15.3比特（理想应该是16bites），当明文长度取值64比特时，Eve恢复明文时的错误比特数大约为30比特（理想应该是32比特）， 我给出的解释是，当输入长度增大时，也相当于数据结构变复杂，而此时的网络架构对于输入数据就会显得简单，处于‘欠拟合’状态。可是在 对称密码中，如果分组长度为16的话，过于短小，一般为128bits，所以可以适当增加网络复杂度。