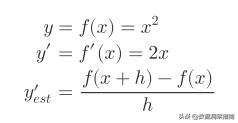机器学习基础:理解梯度下降本质「附Python代码」
https://www.toutiao.com/a6646958932096975373/
2019-01-16 13:15:26
今天我们尝试用最简单的方式来理解梯度下降,在之后我们会尝试理解更复杂的内容,也会在各种各样的案例中使用梯度下降来求解(事实上之前线性回归模型中我们已经使用了它),感兴趣的同学欢迎关注后续的更新(以及之前的内容)。
梯度下降的原理
在数据科学中,我们经常要寻找某个模型的最优解。梯度下降就是数值优化问题的一种方案,它能帮助我们一步步接近目标值。在机器学习过程中,这个目标值往往对应着“最小的残差平方和”(比如最小二乘法求解线性回归)、“最大的似然”(比如极大似然估计求解逻辑回归)等。
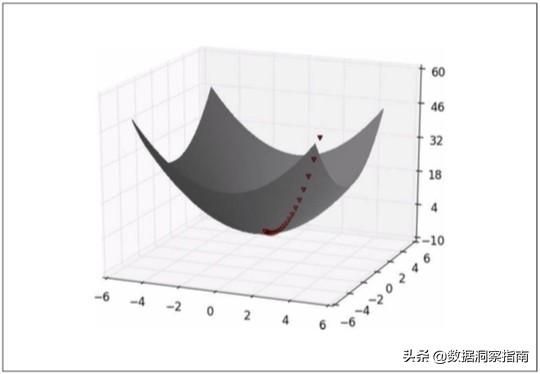
在实际应用的过程中,梯度给出了我们数值调整的方向,一般来说,它对应着微积分中的偏导数,在这个方向上,我们的数值优化速度最快。我们用下图来理解一下梯度下降的过程:
假如我们的目标是寻找全局最小值,最上边的红三角是我们的起始点。那么梯度下降的过程就是先寻找起始点的导数方向,然后在这个方向上迈出一步,到达第二个点;然后计算第二个点的导数,接着迈出第二步,到达第三点……直到我们的目标值不再变化或者变动值小于某个阈值,那我们就认为我们找到了最小值或近似的最小值(只要设定好阈值,两者的差异几乎可以忽略不计)。
在上图中,每个小三角都对应着梯度下降过程中的一个循环(计算导数方向->迈步->满足停止条件则终止循环,否则进入下一个循环)。
梯度的计算
在实际的应用过程中,我们常常是无法直接得到导数的,但是我们可以用两个间隔非常小的点之间连线的斜率来作为替代,根据微分的知识我们可以知道,当间隔趋近于0时,斜率趋近于导数,当间隔小到一定程度时,两者的差异已经可以忽略不计。
我们用最简单的平方函数来演示一下,很容易知道,平方函数、平方函数的导数函数以及估计导数分别为:
那么我们用Python来对比一下两种方法得到的导数之间的差异(为了看起来格式规整,同时大家又能复制代码直接使用,所以这里同时提供源码和截图):
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl
from functools import partial
# 定义一个函数,根据数组返回其平方和
sns.set()
mpl.rcParams['font.sans-serif'] = 'WenQuanYi Micro Hei'
# 定义一个函数,根据数组返回其平方和
def square(x):
return x ** 2
# 导数
def derivative(x):
return 2 * x
# 用微分来估计
def diff_quotient(f, x, h):
return (f(x + h) - f(x)) / h
# 偏函数
der_esti = partial(diff_quotient, square, h=0.00001)
# 生成测试数据
x = list(range(-10, 10))
# 绘图
plt.figure(figsize=(8, 6))
# 计算并绘制实际导数数据
plt.plot(x, list(map(derivative, x)), 'r+',
markersize=12, label='实际导数值')
# 计算并绘制估计导数数据
plt.plot(x, list(map(der_esti, x)), 'gx',
markersize=12, label='估计导数值')
plt.legend()
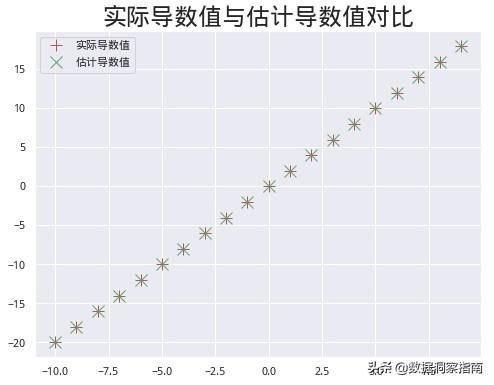
plt.title('实际导数值与估计导数值对比', fontsize=24);
两者差异微乎其微,不是吗?当然,这里我们的例子是最简单的一元函数,事实上,在数据科学过程中,我们往往会遇到包含大量特征的情况,这时就需要针对每个特征的系数计算其偏导数。这一部分我们留作之后为大家讲解,心急的同学也可以自己尝试一下。
通过梯度下降求解最小值
还是以平方函数求解最小值为例,前边我们已经完成了梯度的计算公式,那么接下来我们就该输入一个起始点,然后让计算机开始循环求解了。
# 尝试一系列步长,选择目标函数值最小的步长作为最终选择
for alpha in [0.1, 0.01, 0.001, 0.0001, 0.00001]:
# 设置起始点
x = 10
# 设置阈值,当两次计算得到的y值差异在阈值范围内时,终止循环
threshold = 0.000001
#设置初始y值
y_last = y_current = 0
# 设置初始循环次数为0
loop_cnt = 0
# 开始计算
while True:
# 计算当前y值和循环次数
loop_cnt += 1
y_last = y_current
y_current = square(x)
# 如果满足条件,则终止循环,输出数据
if abs(y_current - y_last) < threshold:
print(x, y_current, loop_cnt)
break
# 不满足条件,则计算梯度,
# 更新x,进入下一个循环
gradient = der_esti(x)
x -= gradient * alpha
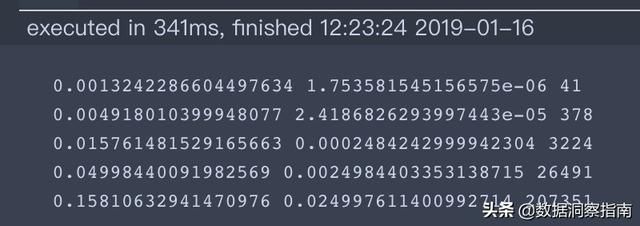
输出为:
0.0013242286604497634 1.753581545156575e-06 41
0.004918010399948077 2.4186826293997443e-05 378
0.015761481529165663 0.0002484242999942304 3224
0.04998440091982569 0.0024984403353138715 26491
0.15810632941470976 0.024997611400992714 207351
可以看到,在步长为0.1时,我们得到了最小值。这样我们就完成了一个简单的梯度下降求解最小值的案例,有问题的同学可以在下方留言,我会及时回答。