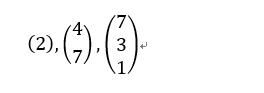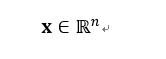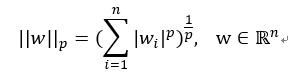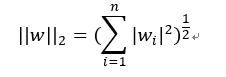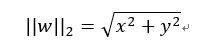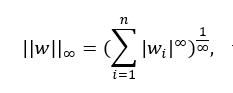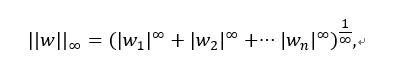机器学习中的数学基础（1）——向量和范数

https://www.toutiao.com/i6668553958534939144/

从今天开始，我将开设一个机器学习数学基础的系列。主要介绍机器学习中经常用到的那些数学知识，方便大家入门。一说起数学，有人会觉得很难。其实在这个系列中，我将会以最直白的语言来向你解释这些数学名词，大家不用担心，即使你是零基础，一样可以看得懂。

• 向量

我们从向量开始说起，什么是向量？它其实就是用括号括起来的一堆数，只不过这些数都是竖着写的。比如：

 

它们就分别是1维、2维和3维的向量。我们一般用小写粗体来表示向量，如x。如果我们写

 

它代表什么含义呢？“∈”这个符号读作属于，R表示实数集，而n表示维度。也就是说向量有几个元素，就是几维的向量。整个式子表示：向量x有n个维度，每个元素的取值都在实数集中。

• 范数

范数，又叫做L-p范数。它是这么定义的：

 

看上去很复杂，其实也容易理解，我们一点点来看。上面的式子是说，对于给定的一个n维向量w，它的范数就是向量w中的各个元素的绝对值的p次方之和，再开p次的根号（1/p就相当于开p次根号）。根据p的取值不同，范数的结果也就不同。我们常用的p值为1,2，∞等等。

1. L1范数

我们先来看p值为1时的范数，我们称之为L1范数。把p=1代入上面的式子，得到：

 

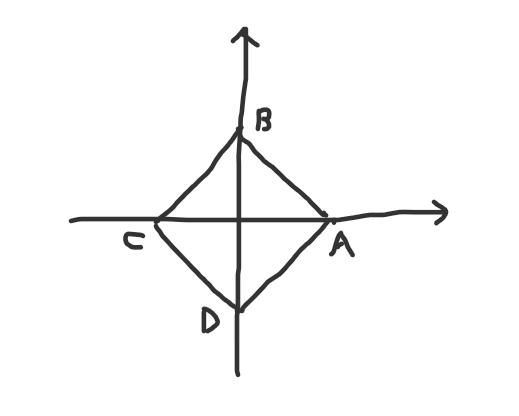
可能上面的式子还不够直观，我们再举个例子来看。假设我们有二维向量w=（x，y），那么w的L1范数就是|x|+|y|。当范数值固定时，我们还可以画出由所有的点（x，y）构成的图像。这里不妨假设|x|+|y|=1（当然你可以假设为任意值k，这里假设为1只是为了画图方便），我们大概用手画一下它的图像：

图1

 

那么图像为什么是这样子的呢？我们可以研究下公式|x|+|y|=1，其中x和y的正负性是未知的，我们就可以分情况来讨论：

① x>0，y>0。公式化简为x+y=1，它原本的图像是过图1中A、B两点的直线，但现在约束条件是x、y均大于0.所以它最后的图像就是AB线段。

② x>0，y<0。公式化简为x-y=1，它原本的图像是过图1中A、D两点的直线。但现在有了约束条件，所以它最后的图像就是AD线段。

③ x<0，y>0。公式化简为-x+y=1，它原本的图像是过图1中B、C两点的直线。但在约束条件下，它最后的图像为BC线段。

④ x<0，y<0。公式化简为-x-y=1，它原本的图像是过图1中C、D两点的直线。但在约束条件下，它最后的图像变成CD线段。

综合以上的4种情况，|x|+|y|=1最后的图像就是由AB、AD、BC、CD一共4条线段构成。

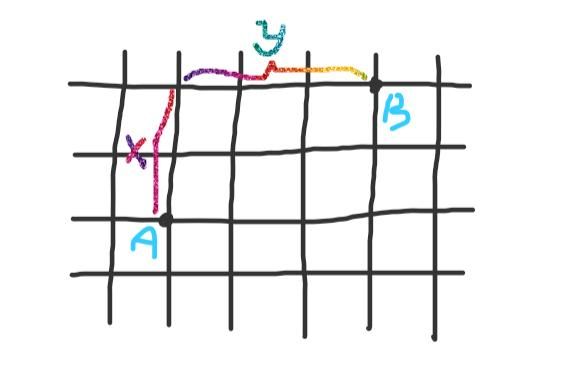
另外，我们也把L1范数称为曼哈顿距离。为什么呢，我们画个图来看下：

曼哈顿街道（图2）

 

美国曼哈顿的街道一般都是横平竖直的，从上图中可以看出，我们想从A点到B点，无论我们如何选择路线行走，最后走过的距离都是x+y。

2. L2范数

当p值为2时，代入范数定义公式，可得到L2范数：

 

注意，L2范数右下角的小标2是可以省略的，也只有L2范数才能省略。我们还是用向量w=（x，y）来举例说明，则上式为：

 

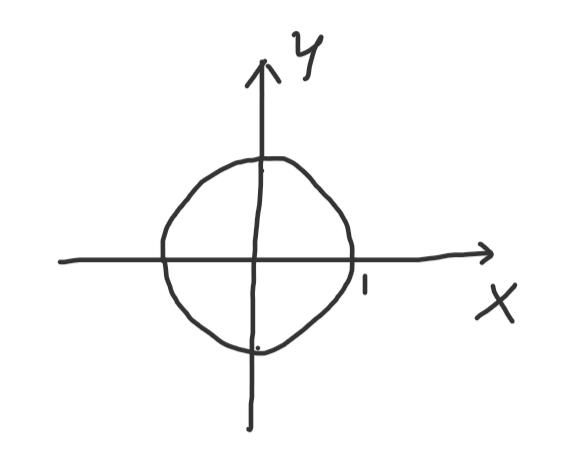
这里我们不妨再假设w的范数值为1，则有x²+y²=1.这就是单位圆的方程啊，我们把它画出来：

图3

 

此外，L2范数也被叫做欧式距离。

3. L-∞范数

当p的值取无穷大时，此时的范数又是多少呢？我们一步一步来推导，先把p=∞代入，得到：

 

展开，可得

 

我们先来关注括号内的部分，对于W1到Wn，我们总能找到一个Wj，使得Wj在其中是最大值。由于指数增长是非常快的，那么在求它们的∞次方的时候，括号内的值可以被看做是求Wj的∞次方。然后再对它开∞次的根号，最后得到的就是|Wj|。因此，我们就得到：

 

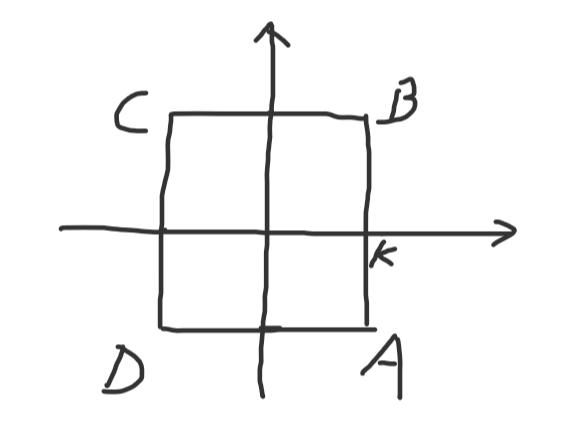
其中，Wj是向量w元素中的最大值。我们还是以向量w=（x，y）举例，来画出L-∞范数下的图像：

 

可以看到，最后的图像是一个正方形。那为什么是这样呢？我们还是分情况来讨论：

① x取到最大值k，且x>0。也就是说x=k，那么图像就是AB线段。

② x取到最大值k，且x<0。结果是x=-k，那么图像就是CD线段。

③ y取到最大值k，且y>0。则y=k，图像是BC线段。

④ y取到最大值k，且y<0。则y=-k，图像为DA线段。

综合以上4种情况，最后的图像就是一个ABCD所构成的正方形了。

以上的内容，你都明白了吗？有问题可以私信我。