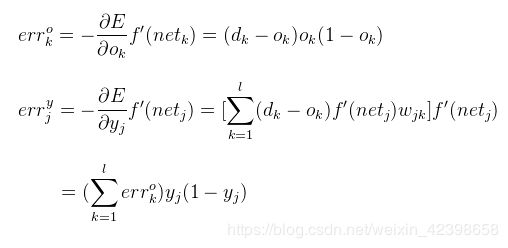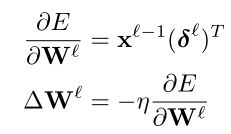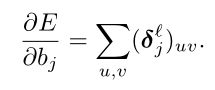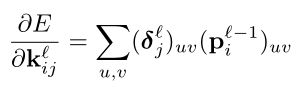深度学习 --- 卷积神经网络CNN（LeNet-5网络学习算法详解）

上一节我们详细探讨了LeNet-5网络的架构，但是还没有解释该网络是如何进行学习的，如何更新权值的，本节将接着上一节进一步CNN的学习机制和权值更新过程，这里请大家一定要对CNN网络有一个清晰的认识，知道每一层是做什么的，为什么这样设置。原因在哪等。大家在学习的过程中需要多问自己几个为什么，这样才能快速进步的，好，废话不多说，开始今天的内容：

        我们知道了CNN其实主要组成部分为卷积层、池化层（下采样层）、BP层、输出层（径向基层）,虽然叫卷积神经网络但是他的学习算法依然是基于BP的，只是和纯BP的算法有所不同的是，这里的权值存在权值共享和激活函数有所不同，但是大体思路还是BP的，因此大家理解时要时刻想到BP的学习原理和权值更新过程。本节将主要参考一个学习笔记即《Notes on Convolutional Neural Networks》，里面的公式肯能和前面的公式不一样，但是意义都是一样的，这里大家需要适应符号的变化。

下面先给出BP的权值调整流程，不懂的建议看我的这篇文章：

误差信号和权值更新如下：

权值更新：

 这里大家需要结合上图和公式深入理解BP的反向传播的原理，尤其是误差信号和权值更新是如何进行的。

 

通过那篇学习笔记我们总体回顾一下BP，因为主要参考的是那篇笔记，因此需要好好的看懂文章里的公式符号：

BP网络回顾：

                                             

上式就是误差函数了，其中N代表样本个数，c代表分类个数，表示是目标值第n个样本的类别为k，表示网络的输出的值第n个样本的类别为k，就是代表N个样本的总误差函数了。为了方便，这里我们取一个样本进行讲解，因此上式就可以写成：

                                             

 对于普通的全连接层的输入和输出通过激活函数可表示为;

                                              

其中表示层的神经元权值和，为激活函数，表示层输出

因为前面已经详细讲解了BP的过程，这里只给出结果，下面是对偏置值求偏导：

                                            

其中，由此可知对偏置值的偏导数就等于误差对权值求和的偏导，所以有下式：

                                             

上式就是往前传播的误差信号，其中是向量的对应位相乘（100维和100维向量圆乘还是100维），下面看一下最后一层的表示：

                                               

输出层有多少维，那么就是多少维，是向量，这里大家需要理解。

通过上面的两个式子，一旦我们知道最后一层的误差信号就可以通过迭代反向传播误差信号了，那么权值如何更新呢？

                                            

其实这些和我们前面的BP分析是一样的，只是符号不同罢了，不理解的建议停下参考我的这篇文章好好自己把BP推一遍。

上面就是BP的简单过程，如果深入理解BP的话，这里看起来还是很容易的。下面就开始我们今天的主题，这里先把LeNet-5网络的在拿过来如下：

 

大家结合这两个图来看，这里都是一样的，我们下面今开始今天的主题，先从卷积层的学习规则开始;

 卷积层：

     这里需要和大家好好解释这个公式和公式中代表的符号，首先需要明确的是这是针对卷积层的， 代表层，这里是卷积层，那么卷积层的上一层和下一层就使用和   表示，至于上下两层分别是什么，都有可能如C3的上一层就是池化层S2，下一次为S4也是池化层。而C1的上一层就是输入了，下一层就是S2池化层，请结合下图理解。

表示卷积的第个特征平面（例如C3就有6个特征平面，C5有120个特征平面） 

表示上一层的第 个平面，因为卷积层的第个平面的神经元对应上一层的平面不止一个如C3对应上一层是3个、4个、6个，此时使用表示，卷积层第平面需要上一层多个平面。

表示卷积层上一层的第个输出，在卷积层就是输入了，是矩阵

表示上一层平面和本层的第特征平面的权值向量   ，是矩阵

是本层的第个特征平面的偏置

求和的原因就是可能是上一层的多个平面对应本层一个平面的意思

上面简单来说就是卷积层的输入和输出的表示。这里大家结合图应该可以很好的理解卷积层是如何表示的。

卷积梯度

这里介绍卷积层的信号如何往回传播，公式如下：

                                                  

这里我们知道的是，,但是不知道和up，其实是卷积层的下一层即采样层（池化层）的系数，那UP是什么呢？我们知道卷积层下一层是采样层又称下采样层即down表示，那么up就表示从采样层到卷积层的操作即上采样，下采样后一般不可逆，但是可以近似，这里通过 Kronecker函数进行反向生成，为什么要进行这一步操作呢？因为在CNN的卷积层到采样层是数据压缩，权值共享，同时卷积层的误差信号和下一次的误差信号有关，因此需要下一层即采样层反向传给卷积层，但是此时的维度不一样，即权值维度是不同的，如何解决呢？这里就是同过 下面的公式进行生成，生成公式如下：

大家不要理解太麻烦其实很简单，如下，

 

我们采样过程是把维度降低了，他的反向过程就是增加维度，因此就按照上面的进行就可以了，很简单吧。

我们在分析上面的式子，会发现卷积层的第个特征平面的误差信号等于本层通过激活函数求导圆乘（对应位相乘）上采样矩阵，然后在乘上一个常数。这里大家要时刻和上面的BP进行比较理解

此时我们看看学习信号：      和上面的BP类似，对偏置值求偏导就是学习梯度了

                                                                

这一句是什么意思呢？就是把矩阵的所有元素求和就可以了。就这么简单。   

再看看权值是如何更新的：

                                                               

这个函数不好理解，那篇文章也没有说清楚，挺复杂的，为了解释这个式子他给出了MATLAB的实现代码：

                                                               

这句代码也不好理解，这里先看rot180里面的式子，其中conv是2维卷积计算，输入为  是上一层的第i个平面的输出，rot180（）  意思是把旋转180°角，然后和做卷积，Valid是什么意思呢？这里为了让大家明白，我再次细致分析，上面是按照论文过来的，基础不好的可能头大，主要难点是在于1.本层是卷积层，下一层是采样层，在知道采样层误差的情况下计算卷积层的误差，和更新权值。2本层是采样层，下一层是卷积层，在知道卷积层的误差信号时，计算采样层的误差信号和权值更新。下面按照我的理解进行深入解释：

输出层的残差：

                            

这个很简单，不解释了 。

下一层为采样层（subsampling）的卷积层的残差：

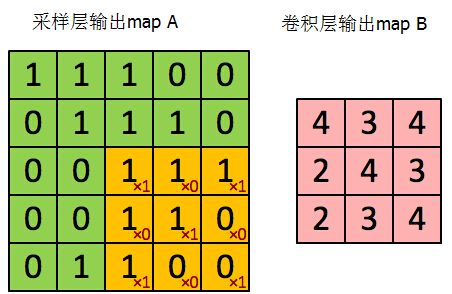
当一个卷积层L的下一层(L+1)为采样层，并假设我们已经计算得到了采样层的残差，现在计算该卷积层的残差。从CNN网络可以看出采样层（L+1）的map大小是卷积层L的1/（2x2），但这两层的map个数是一样的，如C1和S2，其中C1是28x28的，采样窗口为2x2的，结果采样层为14x14，但是层数都是6。也就是说卷积层的某个平面的四个神经元对应采样层的某个平面的一个神经元。因此此时知道采样层的残差信号为14x14的，但是卷积层的输出维度为28x28的，如果想要把采样层的残差信号传给卷积层，则需要对采样层的残差维度进行扩容，使其和卷积层的输出map一致，怎么办呢？使用克罗内克积进行扩充：如下图

通过这样的方式就 可以是其维度一致了，然后和卷积层的输出向量进行按位相乘，如下（这里加入残差为2x2的，卷积层的输出为4x4的）：

这样就得到卷积层的残差信号了，这一层的地推公式就是下式了：

那么我们下面讨论如果这一层为采样层，下一层为卷积层，残差是如何计算的。

下一层为卷积层（subsampling）的采样层的残差

当某个采样层L的下一层是卷积层(L+1)，并假设我们已经计算出L+1层的残差，现在计算L层的残差。采样层到卷积层直接的连接是有权重和偏置参数的，因此不像卷积层到采样层那样简单。现再假设L层第j个map Mj与L+1层的M2j关联，按照BP的原理，L层的残差Dj是L+1层残差D2j的加权和，但是这里的困难在于，我们很难理清M2j的那些单元通过哪些权重与Mj的哪些单元关联，也是上面的那个说不清的式子即：

                                           

论文里通过MATLAB进行解释，如下：

                                              

这里我们也按照MATLAB进行解释吧：

rot180表示对矩阵进行180度旋转（可通过行对称交换和列对称交换完成），为什么这里要对卷积核进行旋转，答案是：通过这个旋转，'full'模式下得卷积的正好抓住了前向传输计算上层map单元与卷积和及当期层map的关联关系，需要注意的是matlab的内置函数convn在计算卷积前，会对卷积核进行一次旋转，因此我们之前的所有卷积的计算都对卷积核进行了旋转：

a =
    1     1
    1     1
    1     1
k =
    2     3
    5     6
    8     9

>> convn(a,k,'full')
ans =
    3     6     5     3
   12    21    16     9
   27    45    33    18
   24    39    28    15
   15    24    17     9

convn在计算前还会对待卷积矩阵进行0扩展，如果卷积核为k*k，待卷积矩阵为n*n，需要以n*n原矩阵为中心扩展到(n+2(k-1))*(n+2(k-1))，所有上面convn(a,k,'full')的计算过程如下：

实际上convn内部是否旋转对网络训练没有影响，只要内部保持一致（即都要么旋转，要么都不旋转），所有我的卷积实现里面没有对卷积核旋转。如果在convn计算前，先对卷积核旋转180度，然后convn内部又对其旋转180度，相当于卷积核没有变。

为了描述清楚对卷积核旋转180与卷积层的残差的卷积所关联的权重与单元，正是前向计算所关联的权重与单元，我们选一个稍微大一点的卷积核，即假设卷积层采用用3*3的卷积核，其上一层采样层的输出map的大小是5*5，那么前向传输由采样层得到卷积层的过程如下：

 

大家把这两个点理解清楚了，基本CNN的网络权值更新就基本搞懂了。下面我按照论文把其他层更新也简要介绍一下。

采样层： 

 这个不解释了，在上面详细介绍了，这里直接把公式复制过来。

其它层基本上是全连接的，和BP是一样的了。这里就不详细说了。到这里本节结束。下一节介绍另外一种网络 深度卷积神经网络。