吴恩达机器学习编程题ex1上 单变量线性回归： (python版含题目要求、代码、注解)

不得不说安卓老师是真的用心良苦，给我们把编程题弄成了填空题，但是很可惜原版使用的是Octave和MATLAB所以作为初学者我就直接当编程题用python去做了

问题：让你绘制一个5阶单位阵

答案：

 

 

在本练习的这一部分，你将应用线性回归来实现通过用一个变量x（人口）预测y(食品卡车的利润)。假设你是一位首席执行官，餐饮连锁店正在考虑不同的城市开设新的出口。这个连锁已经把卡车开到了各个城市，现在你有来自城市的利润和人口的数据了。你希望使用这些数据来帮助你选择扩展哪个城市。

你希望通过这些数据来辅助你决定下一步选择扩展哪个城市。

文件EX1DATA1.TXT包含了我们的线性回归问题的数据集。第一列是城市的人口，第二列是那个城市的食品卡车的利润。利润的负值表示损失。

 

 

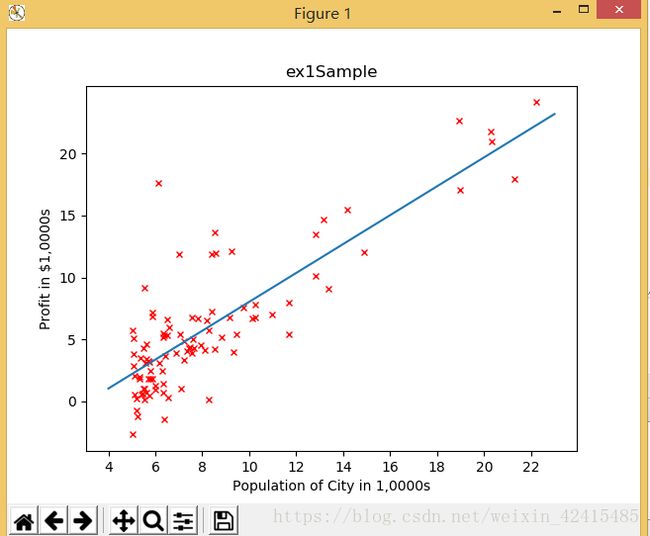
在开始任何任务之前，通过数据可视化来理解数据是有很有用的。对于这个数据集，可以使用散点图来可视化他。因为它只只有两个属性需要绘制（利润和人口）。

而在现实生活中你会遇到很多其他问题是不能在二维图上绘制的。

在EX1.M中，将数据集从数据文件加载到变量X中和Y：

问题：让你绘制一个数据集的散点图

答案：

 

在这一部分中，你将采用梯度下降法通过线性回归找到合适的参数θ去拟合到我们的数据集。

这里题目写的是θ^tx就是 1*2  *  2*m 我们为了编程中方便观察（如果x有m列那看起来就太糟糕了）把x写成m行2列的形式 其实就是题目中的（θ^tx）^t

 

为数据添加θ0这个截距项（线性方程的常数项）的维度并将θ初始化为0，设置学习速率为0.01，迭代次数为1500

 

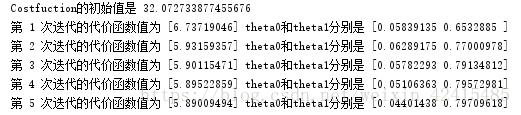
当你执行梯度下降最小化代价函数时，通过计算代价值将帮你监控收敛性，计算代价函数 在你做的时候切记x和y不是标量而是代表训练集的行矩阵，当θ为初始值时这个函数执行出来的结果是32.07

 

 

接下来你将对文本执行梯度下降 安卓老师已经帮我们写好了循环结构 只需要我们填空（再次为老师点赞是真的良心）我们想要把J(θ)降到最小 当你更新参数时切记是更新x、y的向量而不是一个x、y的参数值 如果你忘了怎么做 请你回看视频 一个好的方法去检验梯度下降法是否正常工作：每次迭代都会调用函数computeCost去检验费用 如果你的方法正确那么费用绝对不会增加 并且在算法接近最后的时候 J(θ)会逐渐收敛到一个值 你的最终价值将用于预测这些人口面积在3W5和7W之间的对应利润 注意下面几个TIPS： 使用的是矩阵乘法而不是数字运算

吴恩达再次强调你要做的是向量运算而不是数值运算

 

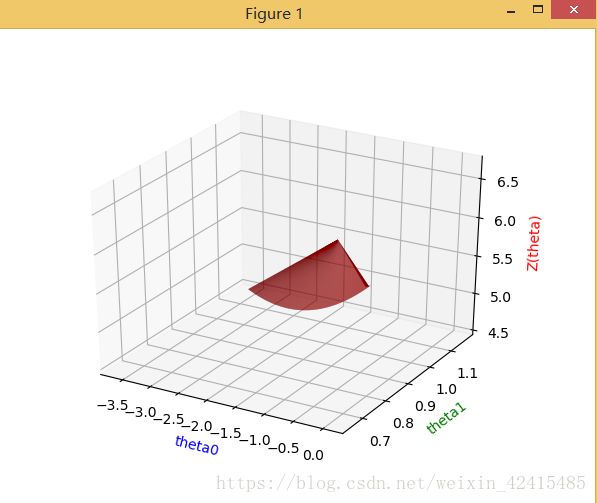
为了更好地理解代价函数 现在你将绘制θ0和θ1二维网格图。在这部分 你不需要编写任何新的代码 但是你应该理解你是如何这些代码是如何绘制这些图像的。

在代码执行后会生成上述图像

这些图表的目的是向你展示J (θ)是如何随θ0和θ1的变化而变化的。成本函数J (θ)是碗形的 具有全局最小值(在等高线图中比在3D曲面图更容易看出)这个最小值对应的是θ0和θ1就是θ0、θ1的最优点 并且梯度下降的每一步都更接近这个点。

完整代码及注解

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def warmupExercise():
    E5 = np.eye(5)  # eye(5)代表5阶单位阵
    print('这是一个五阶单位阵')
    print(E5)

def plotDatainit(x, y):

    plt.title('ex1Sample')#图的标题
    plt.plot(x, y, 'rx', ms=5)#ms=5代表散点大小为5个单位
    plt.xticks(np.arange(4,24,2))#设置x轴的尺度（这里和吴老师在pdf上绘制一致从4开始24结束，2为组距）
    plt.yticks(np.arange(-5,25,5))#设置y轴尺度
    plt.xlabel('Population of City in 1,0000s')#横轴的含义：x:城市人口
    plt.ylabel('Profit in $1,0000s')#纵轴含义y:收益
    plt.show()

def plotData(x, y,theta0,theta1):

    plt.title('ex1Sample')#图的标题
    plt.plot(x, y, 'rx', ms=5)#ms=5代表散点大小为5个单位
    plt.xticks(np.arange(4,26,2))#设置x轴的尺度（这里和吴老师在pdf上绘制一致从4开始24结束，2为组距）
    plt.yticks(np.arange(-5,25,5))#设置y轴尺度
    plt.xlabel('Population of City in 1,0000s')#横轴的含义：x:城市人口
    plt.ylabel('Profit in $1,0000s')#纵轴含义y:收益
    x = np.arange(4, 24)
    y = theta0+theta1*x
    plt.plot(x, y)
    plt.show()

def computeCost(X,y,theta,num):
  m=num
  result=np.sum((np.dot(X,theta)-y)**2)/(2*m)#计算假设函数的值
  return result

def gradientDescent(X,y,theta,num,studyrate,iterations):
    m=num
    J_every=np.zeros((iterations,1))#用于存储每次迭代计算出的costfunction值
    theta_every=np.zeros((interations,2))
    XT=X.T#为保证矩阵乘法行列要求 接下来计算会用到X的转置
    for i in range(interations):
        #dJdivdtheta = np.sum(np.dot(XT,((np.dot(X, theta) - y))/m )) #这是错的
        dJdivdtheta = (np.dot(XT,((np.dot(X, theta) - y))/m ))#这是对的
        theta = theta - studyrate * dJdivdtheta
        theta_every[i][0]=theta[0][0]
        theta_every[i][1]=theta[1][0]
        J_every[i] = computeCost(X, y, theta,num)
    return theta,J_every,theta_every

def showCostfunction(interations):
  for i in range(interations):
    print('第',i+1,'次迭代的代价函数值为',costhistory[i],'theta0和theta1分别是',thetahistory[i])

def predictProfit():
  predict1=np.dot(np.array([1,3.5]),thetai)#预测3.5W人口的利润
  predict2=np.dot(np.array([1,7]),thetai)#预测7W人口的利润
  print("3W5人口利润是",(predict1[0]*10000))
  print("7W人口的利润是",(predict2[0]*10000))

def plot3DJtheta():
    import matplotlib.pyplot as plt
    from mpl_toolkits.mplot3d import Axes3D
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    xx=list(thetahistory[:,0])#把thetahistory的第1列即使theta0变成一个1500个元素组成的列表
    yy=list(thetahistory[:,1])#把thetahistory的第2列即使theta1变成一个1500个元素组成的列表
    zz=costhistory.reshape(1500)#把costhistory形状弄成1500个的横着的
    # 网上抄的如上
    ax.set_xlabel("theta0", color='b')
    ax.set_ylabel("theta1", color='g')
    ax.set_zlabel("Z(theta)", color='r')
    ax.plot_trisurf(xx, yy, zz,color='red')
    plt.show()

def plotContour(thetai,X,y,num):#这个函数是网上抄的-0-
    theta0_vals = np.linspace(-10, 10, 100)
    theta1_vals = np.linspace(-1, 4, 100)
    J_vals = np.zeros((len(theta0_vals), len(theta1_vals)))
    for i in range(len(theta0_vals)):
        for j in range(len(theta1_vals)):
            t = np.array([theta0_vals[i], theta1_vals[j]]).reshape((2, 1))
            J_vals[i, j] = computeCost(X, y, t, num)
    J_vals = J_vals.T
    # fig = plt.figure()
    # ax = Axes3D(fig)
    # ax.plot_surface(theta0_vals, theta1_vals, J_vals, rstride=1, cstride=1, cmap='rainbow')
    # plt.xlabel('theta_0')
    # plt.ylabel('theta_1')
    # 这部分是3D图
    # 填充颜色，20是等高线分为几部分
    plt.contourf(theta0_vals, theta1_vals, J_vals, 20, alpha=0.6, cmap=plt.cm.hot)
    plt.contour(theta0_vals, theta1_vals, J_vals, colors='black')
    plt.plot(thetai[0], thetai[1], 'r', marker='x', markerSize=10, LineWidth=2)  # 画点
    plt.show()


warmupExercise()
dataset=np.loadtxt('ex1data1.txt',delimiter=',')#读取数据集文本
xx=dataset[:,0]#取出文本的第一列
yy=dataset[:,1]#取出文本的第二列
num=len(xx)
#print(num) #看看有多少个x (有97个数据)
x=xx.reshape(num,1)#转成num行的列向量
y=yy.reshape(num,1)#同上
thetainit=np.zeros((2,1))#由题设theta包含两个参数常数项theta0和一阶系数theta1 后面会更新theta所以初始化是一个空矩阵 是2行1列的矩阵
juzhenx=np.array(x).reshape(len(x),1)#数据集中属性x转换成一个n行1列的矩阵
X0=np.ones((len(x), 1))#因为假设函数是theta0加theta1*x 所以我们后续的计算涉及到矩阵运算
X = np.c_[X0, juzhenx]#把矩阵x(97行1列)拼在X0(97行1列)右边 形成一个97行2列的矩阵X
#X=np.hstack((X0,juzhenx))#这是矩阵拼接的另外一个方法
#print(X)#看看X是否符合要求
#print(X.shape)#看看X行列是否符合要求
studyrate=0.01
interations=1500
print("Costfuction的初始值是",computeCost(X,y,thetainit,num))#查看还未更新的代价函数值
thetai,costhistory,thetahistory=(gradientDescent(X,y,thetainit,num,studyrate,interations))
showCostfunction(interations)
predictProfit()
plotData(x, y,thetai[0],thetai[1])
plot3DJtheta()
plotContour(thetai,X,y,num)

见下