李宏毅机器学习——梯度下降详细讲解
文章目录
- 梯度下降
- 1. 学习率
- 1.1自适应学习率
- 1.2 Adagrad算法
- 2. 随机梯度下降
- 3. 特征缩放
- 3.1 特征缩放原因
- 3.2 特征缩放方法
- 4. 梯度下降的限制
梯度下降
梯度下降是为了解决回归方程中参数的最优化问题,即表现为下述的式子:
θ ∗ = arg min θ L ( θ ) \theta ^{\ast }=\arg \min _{\theta }L\left( \theta \right) θ∗=argθminL(θ)
- L ( θ ) L\left(\theta\right) L(θ) : Lossfunction( 代价损失函数)
- θ \theta θ:parameters(参数)
注意:上述中的 θ \theta θ并不是指的一个参数,而是指的一组参数
需要找一组参数,令代价损失函数的值达到最小值,可以使用梯度下降的方法来寻找参数。
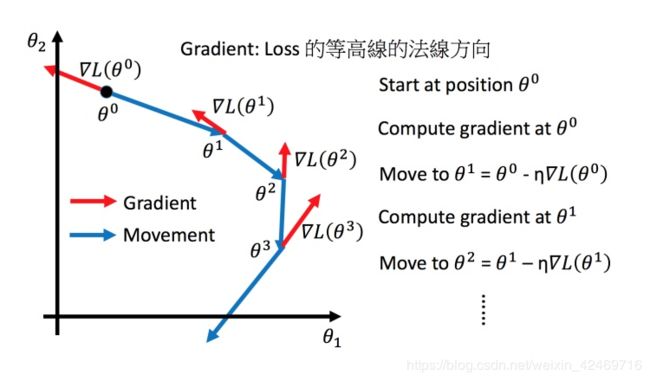
梯度下降方法开始时随机初始化一组 θ \theta θ 值(通常情况下初始化为0),在这里我们假设 θ \theta θ 中是一个二维参数,即包含 θ 1 θ 2 \theta_{1} \theta_{2} θ1θ2 两个参数,如下图:
θ = [ θ 1 θ 2 ] \theta =\begin{bmatrix} \theta _{1} \\ \theta _{2} \end{bmatrix} θ=[θ1θ2]
η \eta η:learning_rate:学习率
∂ L ( θ ) ∂ θ \dfrac {\partial L\left( \theta \right) }{\partial \theta } ∂θ∂L(θ):表示对参数求微分
θ i \theta^{i} θi:表示第 i 此迭代后的参数值
∇ L ( θ ) \nabla L\left(\theta\right) ∇L(θ):表示梯度
1. 学习率
下图表示对学习率的可视化描述:
学习率的选择
学习率在很大程度上影响了梯度下降后的最终参数的取值,从而影响损失函数最终的值,如果学习率 η \eta η 初始化为一个较大的值,可能再开始的时候代价损失的值是下降的,但是之后代价损失可能会突然增加,也可能一开始代价损失的值就会增大。如果学习率初始化为一个较小的值,梯度下降就会执行较长的时间,在时间的花费上让人无法忍受,如下图所示:
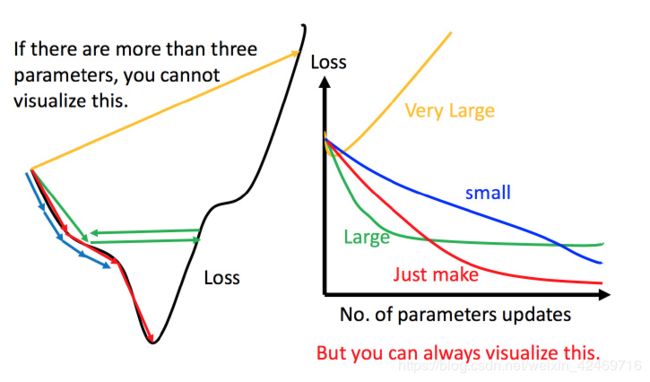
上图左边黑色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
虽然这样的可视化可以很直观观察,但可视化也只是能在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
1.1自适应学习率
上述结果产生的原因是因为学习率在开始时学习率设定初值之后就不变了,从而导致损失函数值的不确定性,我们可以通过一种方式,令学习率随着迭代次数的进行而不断的变化,从而令梯度下降很好的进行。
一个简单的思想上:随着迭代次数的逐渐增加,通过某一些因子来令学习率逐渐的降低,这样的原因是:
1、在梯度下降刚开始时,初始点距离最低点有较远的距离,此时的学习率可以设置的大一点
2、随着迭代次数的增加,点会比较靠近最低点,这个时候应该令前进的步伐小一点,需要设置较低的学习率。
比如使用 η t = η t + 1 \eta^{t}=\dfrac{\eta}{\sqrt{t+1}} ηt=t+1η t表示迭代的次数
1.2 Adagrad算法
Adagrad算法是令当前的学习率等于全局初始的学习率除以当前参数之前所有的微分平方和的均方根
普通的梯度下降:
w t + 1 = w t − η t g t w^{t+1} = w^{t} - \eta^{t}g^{t} wt+1=wt−ηtgt
η t = η t + 1 \eta^{t} = \dfrac{\eta}{\sqrt{t+1}} ηt=t+1η
w t w^{t} wt表示一个参数, g t 表 示 第 t 次 的 微 分 g^{t}表示第 t 次的微分 gt表示第t次的微分
Adagrad相比于普通的梯度下降拥有更好的效果:
w t + 1 = w t − η σ t g t w^{t+1} = w^{t} - \dfrac{\eta}{\sigma^{t}}g^{t} wt+1=wt−σtηgt
σ t = ∑ i = 0 t ( g i ) 2 \sigma^{t}=\sqrt{\sum^{t}_{i=0}\left(g^{i}\right)^{2}} σt=i=0∑t(gi)2
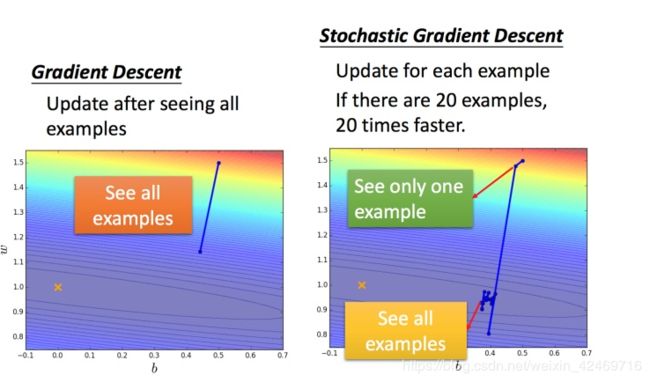
2. 随机梯度下降
普通的梯度下降:
L = ∑ n ( y ^ n − ( b + ∑ w i x i n ) ) 2 L=\sum_{n}(\widehat{y}^{n} - (b+\sum w_{i}x^{n}_{i}))^{2} L=n∑(y n−(b+∑wixin))2
x n = x n − 1 − η ∇ L ( x n − 1 ) x^{n} = x^{n-1} - \eta\nabla L(x^{n-1}) xn=xn−1−η∇L(xn−1)
随机梯度并不是针对所有的数据进行处理,而是随机的选取一个例子 x n x^{n} xn,这种选取方法回事梯度下降处理的更加快速。
随机梯度下降方法如下:
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 L = (\widehat{y}^{n} - (b+\sum w_{i}x^{n}_{i}))^{2} L=(y n−(b+∑wixin))2
x n = x n − 1 − η ∇ L ( x n − 1 ) x^{n} = x^{n-1} - \eta\nabla L(x^{n-1}) xn=xn−1−η∇L(xn−1)
3. 特征缩放
特征缩放针对的是如果一种事物的几种特征之间相差的数量级过大,就会造成数量级小的特征失去作用,比如说下面的函数:
y = b + w 1 x 1 + w 2 x 2 y = b + w_{1}x_{1}+w_{2}x_{2} y=b+w1x1+w2x2
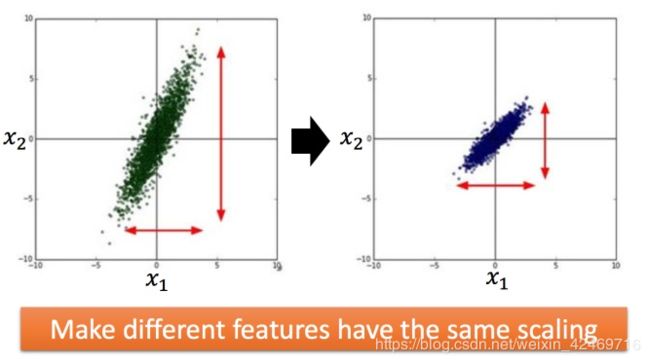
对于 x1 和 x2 特征来说,x1 的分布范围 和 x2 的分布范围不一致,且差别过大,建议进行特征缩放,令两个特征的分布范围相差不大。
3.1 特征缩放原因
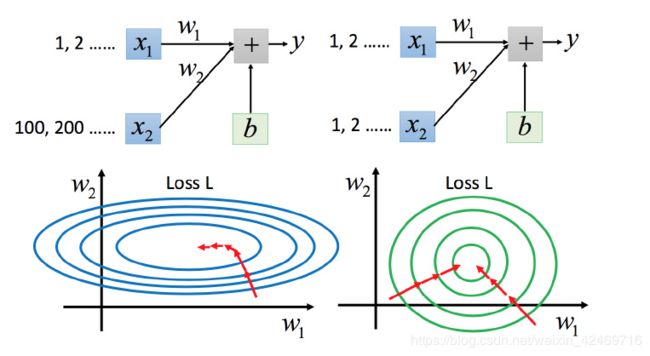
上图左边是 x 1 x_{1} x1 的scale比 x 2 x_{2} x2 要小很多,所以当 w 1 w_{1} w1 和 w 2 w_{2} w2 做同样的变化时, w 1 w_{1} w1对 yy 的变化影响是比较小的, w 2 w_{2} w2对 yy 的变化影响是比较大的。
坐标系中是两个参数的error surface(现在考虑左边蓝色),因为 w 1 w_{1} w1 对 yy 的变化影响比较小,所以 w 1 w_{1} w1对损失函数的影响比较小, w 1 w_{1} w1对损失函数有比较小的微分,所以 w 1 w_{1} w1方向上是比较平滑的。同理 w 2 w_{2} w2对 yy 的影响比较大,所以 w 2 w_{2} w2对损失函数的影响比较大,所以在 w 2 w_{2} w2方向有比较尖的峡谷。
上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也是比较有效率。
3.2 特征缩放方法
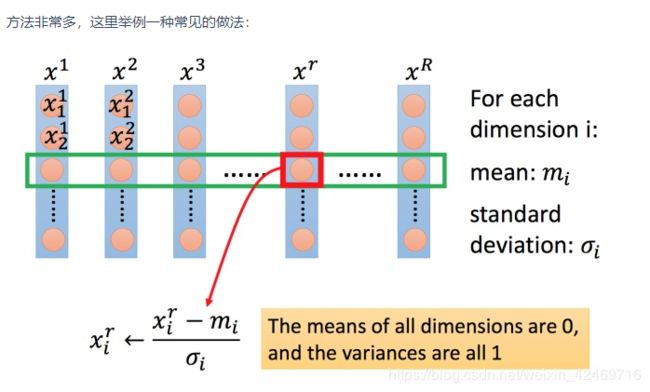
上图每一列都是一个例子,里面都有一组特征。
对每一个维度 i i i(绿色框)都计算平均数,记做 m i m_{i} mi,还要计算标准差,记做 σ i \sigma_{i} σi。然后用第 r r r 个例子中的第 i i i 个输入,减掉平均数 m i m_{i} mi,然后除以标准差 σ i \sigma_{i} σi,得到的结果是第 i i i 个维度的平均值都是 0,所有的方差都是 1。
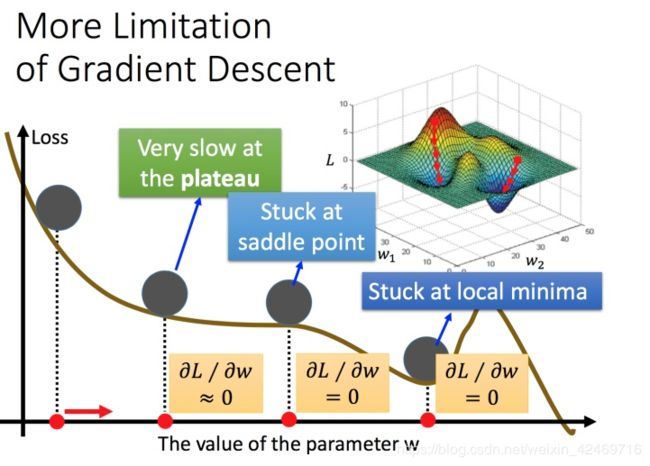
4. 梯度下降的限制
容易陷入局部极值 还有可能卡在不是极值,但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点