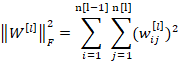吴恩达深度学习第二课第一周作业及学习心得体会——初始化权重、L2正则化、dropout
概述
学习课程后,再第一周第四课作业的基础上完成该周作业,现将心得体会记录如下。
初始化权重
代码更改
在之前的建立神经网络的过程中,提到权重w不能为0,而将它初始化为一个随机的值。然而在一个深层神经网络中,当w的值被初始化过大时,进入深层时呈指数型增长,造成梯度爆炸;过小时又会呈指数级衰减,造成梯度消失。
Python中将w进行随机初始化时,使用numpy库中的np.random.randn()方法,randn是从均值为0的单位标准正态分布(也称“高斯分布”)进行取样。随着对神经网络中的某一层输入的数据量n的增长,输出数据的分布中,方差也在增大。结果证明,可以除以输入数据量n的平方根来调整其数值范围,这样神经元输出的方差就归一化到1了,不会过大导致到指数级爆炸或过小而指数级衰减。
代码更改如下:
- 参数初始化函数:
def init_para(layer_dims, init_mode):
L = len(layer_dims) #L为总层数
np.random.seed(L)
parameters = {}
if init_mode=='zero':
for l in range(1,L): #初始化W1~WL,b1~bL
parameters['W'+str(l)] = np.zeros((layer_dims[l], layer_dims[l-1]))
parameters['b'+str(l)] = np.zeros((layer_dims[l], 1))
if init_mode=='random':
for l in range(1,L): #初始化W1~WL,b1~bL
parameters['W'+str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*0.01
parameters['b'+str(l)] = np.zeros((layer_dims[l], 1))
if init_mode=='norm':
for l in range(1,L): #初始化W1~WL,b1~bL
parameters['W'+str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*np.sqrt(1.0/(layer_dims[l-1]))
parameters['b'+str(l)] = np.zeros((layer_dims[l], 1))
return parameters- 模型函数:
def NN_model(X, Y, layer_dims, learning_steps, learning_rate, print_flag, init_mode):
np.random.seed(1)
costs=[]
parameters = init_para(layer_dims, init_mode) #初始化参数
for i in range(0, learning_steps): #进行learning_steps次训练
AL, caches = prop_forward(X, parameters) #前向传播,计算A1~AL
cost = compute_cost(AL,Y) #计算成本
grads = prop_backward(AL, Y, caches) #反向传播,计算dW1~dWL,db1~dbL
parameters = update_para(parameters, grads, learning_rate) #更新参数
if print_flag==True and i%1000==0:
print('cost at %i steps:%f'%(i, cost))
costs.append(cost)
return parameters,costs
实施效果
二元分类问题1
样本数据集代码如下:
def gendata():
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
Y = np.zeros((m,1)) #初始化样本标签
a = 4 #基础半径
for j in range(2):
ix = range(N*j,N*(j+1))#ix=(0,199)(200,399)
t = np.linspace(j*3.14,(j+1)*3.14,N) #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = a*np.sin(4*t) + np.random.randn(N)*0.4 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
Y[ix] = j #red or blue
return X.T,Y.T令layer_dims=[2,4,3,2,1],learning_steps=20000,learning_rate=0.5。
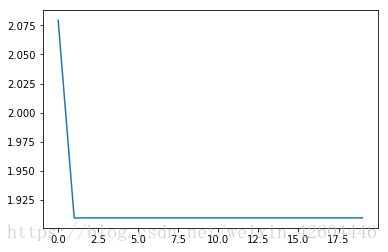
当init_mode='zero'时:
当init_mode='random'时:
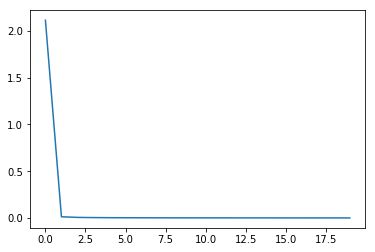
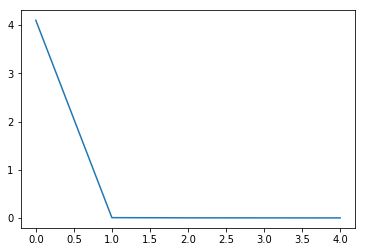
当init_mode='norm'时:
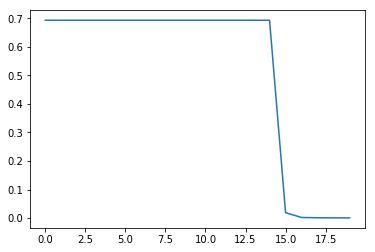
从实施效果可以看到,当初始化参数除以数据量n的平方根,收敛速度明显变快。
二元分类问题2
样本数据集代码如下:
def gendata():
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
Y = np.zeros((m,1)) #初始化样本标签
a = 4 #基础半径
for j in range(2):
ix = range(N*j,N*(j+1))#ix=(0,199)(200,399)
t = np.linspace(0,6.28,N) + np.random.randn(N)*0.1 #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = (a + j*2) + np.random.randn(N)*0.2 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
Y[ix] = j #red or blue
return X.T,Y.T令layer_dims=[2,6,3,1],learning_steps=20000,learning_rate=0.5。
当init_mode='zero'时:
当init_mode='random'时:
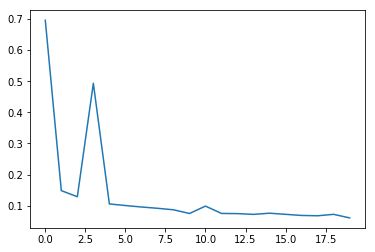
当init_mode='norm'时:
从实施效果可以看到,当初始化参数除以数据量n的平方根,收敛速度明显变快,尤其学习步数太多,最终稍微过拟合。
同时发现,这样初始化参数后,可以将网络深度适当增加(之前增加深度时,总是不收敛),例如将layer_dims=[2,6,3,2,1],运行结果如下:
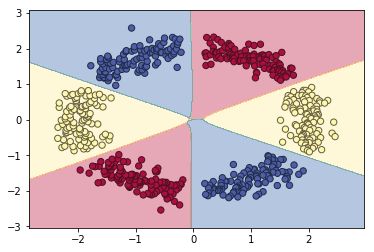
三元分类问题
样本数据集代码如下(y用于sklearn库的逻辑回归,Y用于NN):
def gendata():
np.random.seed(1)
m = 600 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
y = np.zeros((m,1)) #初始化样本标签
Y = np.zeros((m,3)) #初始化样本标签
a = 2 #基础半径
for j in range(6):
ix = range((m//6)*j, (m//6)*(j+1))
t = np.linspace((3.14/3)*j+0.1, (3.14/3)*(j+1)-0.1, m//6) #theta角度,产生200个角度并加入随机数,保证角度随机分开,图像开起来稀疏程度不一
r = a + np.random.randn(m//6)*0.2 #radius半径,4sin(4*t),并加入一定的随机,图像轨道不平滑
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成坐标点
y[ix] = j%3
if j%3==0:
Y[ix] = [1,0,0]
if j%3==1:
Y[ix] = [0,1,0]
if j%3==2:
Y[ix] = [0,0,1]
return X.T,Y.T,y.T预测函数更改如下:
def predict(X,parameters):
AL, caches = prop_forward(X, parameters)
prediction = np.zeros(AL.T.shape)
for i in range(AL.shape[1]):
if np.max(AL[:,i])==AL[0,i]:
prediction[i] = [1,0,0]
if np.max(AL[:,i])==AL[1,i]:
prediction[i] = [0,1,0]
if np.max(AL[:,i])==AL[2,i]:
prediction[i] = [0,0,1]
return prediction.T令layer_dims=[2,18,6,3],learning_steps=20000,learning_rate=0.5。
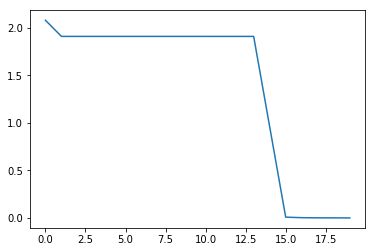
当init_mode='zero'时(注意左图纵坐标范围1.9~2.1):
当init_mode='random'时:
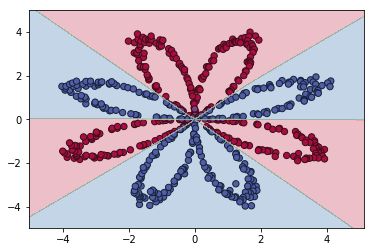
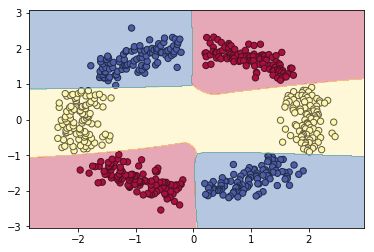
当init_mode='norm'时,网络对二维平面预测结果的对称特性已开始显现:
尝试将网络扩大为layer_dims=[2,288,144,72,36,18,6,3],同时learning_steps=5000,运行结果如下(对称特性明显!):
多元分类问题
在上面的基础上,将训练集改为6类,代码类推即可,不再赘述。
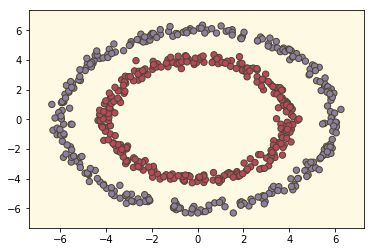
由于训练集无交叉,因此采用sklearn的逻辑回归预测结果也很好。如下图所示。
然后采用NN。令layer_dims=[2,288,144,72,36,12,6],learning_steps=20000,learning_rate=0.5。直接令init_mode='norm',结果如下:
L2正则化
原理
向Logistic回归的成本函数中加入正则化项。
L2正则化:
其中:
L1正则化:
其中:
L1正则化最后得到w向量中将存在大量的0,使模型变得稀疏化,所以一般使用L2正则化。其中的参数λ称为正则化参数,这个参数通常通过开发集来设置。
向神经网络的成本函数加入正则化项:
因为W是一个n[l]×n[l−1]矩阵,所以:
加入正则化项后,反向传播时:
可见W[l]在更新时会多减去一项αλ/m*W[l]。
代码更改
在NN_initpara_1.py基础上(保留参数初始化更改),删除参数初始化模式的选择,强制全为前文的norm类型。文件名“NN_L2Reg_1.py”,其他更改如下。
- 训练集更改(总点数m改为150);
def datagen():
np.random.seed(1)
m = 150 #样本数
N = int(m/2) #分为两类
D = 2 #样本的特征数或维度
X = np.zeros((m,D)) #初始化样本坐标
Y = np.zeros((m,1)) #初始化样本标签
for j in range(2):
ix = range(N*j,N*(j+1))
t = np.random.randn(N)*0.4
r = np.random.randn(N)*0.4
if j==0:
X[ix] = np.c_[t-0.4, r-0.4]
else:
X[ix] = np.c_[t+0.4, r+0.4]
Y[ix] = j #red or blue
return X,Y- 前向传播函数,增加每层W的范数运算,并乘以lambd/2,并对其求和;
#前向传播函数
def prop_forward(X, parameters,lambd):
caches = []
L = len(parameters)//2
for l in range(1,L+1): #l从1到L,调用L次前向运算
if l==1: #第一次运算时,A_pre=X
A_pre = X
else:
A_pre = cache['A']
if l==L: #最后一次运算时,激活函数为sigmoid
mode = 'sigmoid'
else:
mode = 'tanh'
W = parameters['W'+str(l)]
b = parameters['b'+str(l)]
if l==1: #第一次运算时,A_pre=X
L2_SUM = 0
else:
L2_SUM = L2_SUM + 0.5*lambd*np.sum(W*W)
cache = single_forward(A_pre, W, b, mode)
caches.append(cache)
AL = caches[L-1]['A']
return AL, caches, L2_SUM- 损失函数,增加W范数部分的总和(需要除以m);
def compute_cost(AL,Y,L2_SUM):
m = Y.shape[1] #-1/m*[Ylog(A) + (1-Y)log(1-A)]
cost = -1.0/m * np.sum(Y*np.log(AL) + (1-Y)*np.log(1-AL)) + L2_SUM/m
cost = np.squeeze(cost)
return cost- 单次后向运算函数;
def single_backward(dA, cache, mode, lambd):
A_pre = cache['A_pre']
W = cache['W']
b = cache['b']
A = cache['A']
m = A_pre.shape[1]
if mode=='sigmoid': #根据本层激活函数计算本层的dZ
temp = np.multiply(A, (1-A))#sigmoid函数:dZ=dA*[A(1-A)]
dZ = np.multiply(dA, temp)
if mode=='ReLU':
dZ = dA #ReLU函数:A>=0,dZ=dA
for i in range(A.shape[0]): #ReLU函数:A<0, dZ=0
dZ[i,A[i,:]<0] = 0
if mode=='tanh':
temp = (1-A**2) #tanh函数: dZ=dA*(1-A*A)
dZ = np.multiply(dA, temp)
dW = 1.0/m*np.dot(dZ, A_pre.T) + lambd/m*W #根据dZ, A_pre, W计算本层梯度dW db,同时计算dA_pre供前一层反向运算使用
db = 1.0/m*np.sum(dZ, axis=1, keepdims=True)
dA_pre = np.dot(W.T, dZ)
return dA_pre, dW, db- 后向传播函数、模型函数中形参注意也要增加lambd。
实施效果
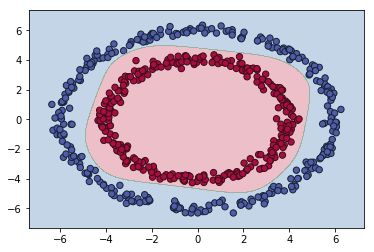
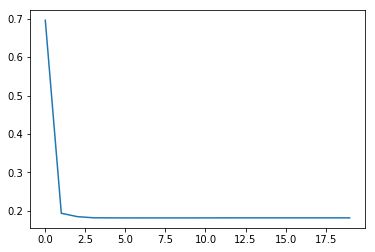
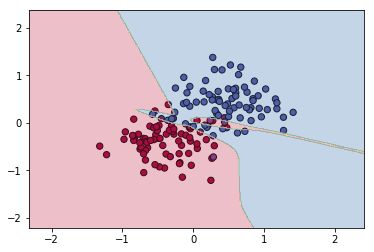
无正则化时(令lambd=0,过拟合):
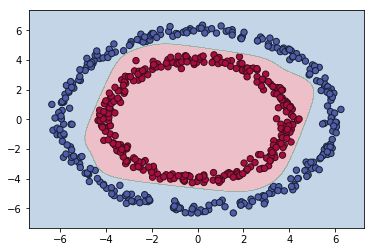
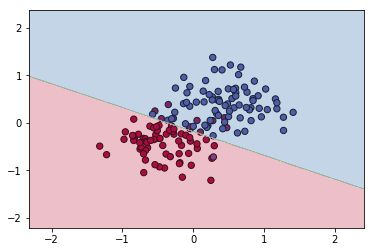
引入L2正则化(lambd=0.5):
dropout
原理
在神经网络中对每层的每个节点预先设置一个被消除的概率,之后在训练随机决定将其中的某些节点给消除掉,得到一个被缩减的神经网络,以此来到达降低方差的目的。
利用dropout,可以简化神经网络的部分结构,从而达到预防过拟合的作用。另外,当输入众多节点时,每个节点都存在被删除的可能,这样可以减少神经网络对某一个节点的依赖性,也就是对某一特征的依赖,扩散输入节点的权重,收缩权重的平方范数。
代码更改
在NN_initpara_1.py基础上(保留参数初始化更改),删除参数初始化模式的选择,强制全为前文的norm类型。文件名“NN_dropout_1.py”,其他更改如下。
- 训练集更改,与前文L2正则化中相同;
- 单次前向运算函数(进行预测时,不能使用dropout,因此增加了“None”分支);
def single_forward(A_pre, W, b, mode, dropout_prob):
if dropout_prob=='None':
Z = np.dot(W, A_pre) + b #根据上一层的输出A_pre,以及本层的W b计算本层的Z
else:
D = np.random.randn(A_pre.shape[0],A_pre.shape[1])- 前向传播函数,增加形参dropout_prob,且在第一层和最后一层不使用dropout;
def prop_forward(X, parameters, dropout_prob):
caches = []
A = X #将X赋给A0
L = len(parameters)//2
for l in range(1,L): #l从1到L-1,调用L-1次前向运算,由于A0的特征值存在大量负数,
A_pre = A #因此第一层激活函数如果选用ReLU无法正确训练网络,因为大量的信息被截掉
if l==1:
A,cache = single_forward(A_pre, parameters['W'+str(l)], parameters['b'+str(l)], 'tanh', 'None')
else:
A,cache = single_forward(A_pre, parameters['W'+str(l)], parameters['b'+str(l)], 'tanh', dropout_prob)
caches.append(cache)
AL,cache = single_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], 'sigmoid', 'None')
caches.append(cache)
return AL, caches- 模型函数和预测函数形参中注意增加dropout_prob。
实施效果
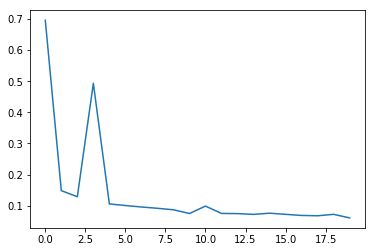
无dropout时(过拟合):
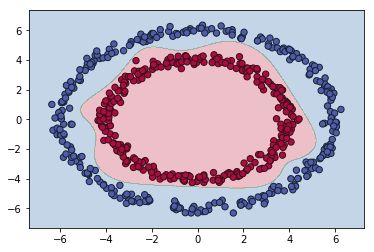
使用dropout时(dropout_prob=0.8):
总结
- 参数(W,b)初始化时,乘以1/(n[l-1])0.5后,可令前向网络的输出与输入保持在同一数量级(如果某层采用的激活函数为ReLU,则应乘以2/(n[l-1])0.5),如此处理有助于训练网络时更快收敛;
- 当网络发生过拟合时,可采用正则化的方法,常用的有L2正则化和dropout。
附
相关代码可以在我的资源中下载!希望能帮到大家!