Simulink仿真SVPWM的一种通用方法
基础知识
SVPWM核心思想就是想让输出的脉宽调制逼近圆旋转磁动势,这在控制电机方面是很重要的。怎么逼近?先假想三个正弦三相波,再假想一个直流电源,根据IGBT桥的8种开关方式可以在空间形成6个扇区,扇区的边界就是空间“基底”,另外还有两种开关方式合成的空间矢量为0,这个0矢量很关键,在利用冲量原则时拿来平衡时间用的。三个假想的正弦波合成一个空间旋转矢量,利用某一时刻矢量所在扇区的两个矢量合成它。
三相转两相
由于要判断扇区和之后利用冲量原理求矢量作用时间,因此要将三相坐标转化为垂直的两相坐标。

利用两相坐标判断合成矢量目前所在扇区
冲量原则求取矢量作用时间

这个冲量原则另外一层含义就是让标准正弦电流合成的磁链与svpwm合成的磁链相同,因为负载为电感的情况下,电流为电压的积分,在小时间段内,积分又等于与时间的乘积,而磁链又是由电流决定的,因此导出使用冲量原则。
不同的扇区作用时间有一定规律性,它们的组成部分都是以下三个时间元:
X = 3 T s U d u β Y = ( 3 2 u α − 1 2 u β ) 3 T s U d Z = ( − 3 2 u α − 1 2 u β ) 3 T s U d X=\frac{\sqrt3T_s}{U_d}u_{\beta}\\ Y=(\frac{\sqrt3}{2}u_{\alpha}-\frac{1}{2}u_\beta)\frac{\sqrt3T_s}{U_d} \\Z=(-\frac{\sqrt3}{2}u_{\alpha}-\frac{1}{2}u_\beta)\frac{\sqrt3T_s}{U_d} X=Ud3TsuβY=(23uα−21uβ)Ud3TsZ=(−23uα−21uβ)Ud3Ts
对应扇区作用时间:
1 : T x = Y , T y = X 2 : T x = − Z , T y = − Y 3 : T x = X , T y = Z 4 : T x = − Y , T y = − X 5 : T x = Z , T y = Y 6 : T x = − X , T y = − Z 1:T_x=Y,T_y=X\\ 2:T_x=-Z,T_y=-Y\\ 3:T_x=X,T_y=Z\\ 4:T_x=-Y,T_y=-X\\ 5:T_x=Z,T_y=Y\\ 6:T_x=-X,T_y=-Z 1:Tx=Y,Ty=X2:Tx=−Z,Ty=−Y3:Tx=X,Ty=Z4:Tx=−Y,Ty=−X5:Tx=Z,Ty=Y6:Tx=−X,Ty=−Z
注意这个地方很多博客包括老师给的PPT都是写错了的,这个应该99%是正确的。
根据X,Y,Z以及之前计算出的扇区就可以得到两个矢量的作用时间,其中Tx是以矢量旋转方向为参考方向反方向的矢量作用时间,Ty是正方向的矢量作用时间。采样时间减去这两个时间就是0矢量的作用时间。
作用时间分配方法
按照开关次数最少原则,使用七段法:
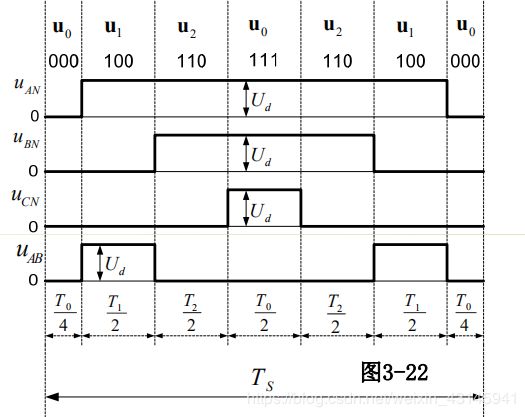
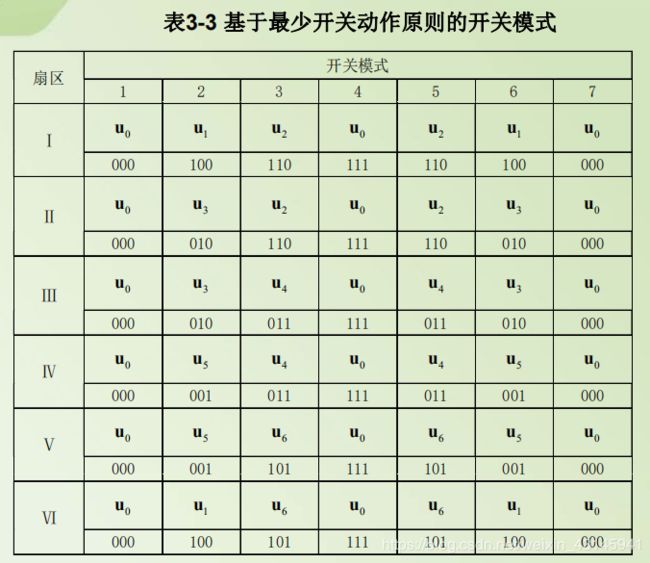
这里注意第2,4,6扇区开始作用的第一个矢量是Ty对应的矢量而不是Tx对应的矢量,因为这样才能满足最少开关次数,否则一次变动需要改变两个桥臂的状态!
我们将扇区分组:135为一组,作用规律为先Tx,后Ty。246为一组,先Ty后Tx。
生成驱动脉冲
这个部分用三角波和三个恒值作比较,当三角波大于时置1:

这个三角波的周期就是之前说的采样周期Ts!并且它的斜率绝对值为1!这样才能生成对应宽度的脉冲。
Simulink仿真
这个模型如果要私聊我,经过了多次修改,结果百分之90以上把握正确。
这个仿真需要注意我们算法模拟的Ud需要和实际逆变直流电源Ud一致,相当于理解为算法Ud在做仿真,也就是仿真中的仿真。(套娃)
Ud不能小,至少 3 U r e f \sqrt3U_{ref} 3Uref,小了会出现矢量“力不从心现象”,无法满足冲量原则!
整体模型:

三相变两相:
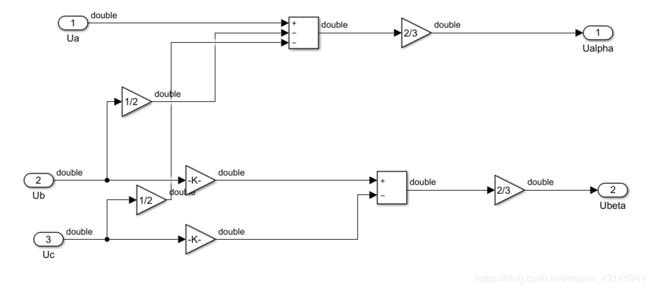
扇区计算函数:
function y = fcn(Ualpha,Ubeta)
y=1;
if Ualpha>=0&&Ubeta>=0&&Ualpha/Ubeta<=sqrt(3)
y=1;
end
if Ubeta>=0&&Ubeta/abs(Ualpha)>=sqrt(3)
y=2;
end
if Ualpha<=0&&Ubeta>=0&&-Ubeta/Ualpha<=sqrt(3)
y=3;
end
if Ualpha<=0&&Ubeta<=0&&Ubeta/Ualpha<=sqrt(3)
y=4;
end
if Ubeta<=0&&-Ubeta/abs(Ualpha)>=sqrt(3)
y=5;
end
if Ualpha>=0&&Ubeta<=0&&-Ubeta/Ualpha<=sqrt(3)
y=6;
end
end
时间组成元X,Y,Z计算函数:
function [X,Y,Z] = fcn(Ualpha,Ubeta,Ud,Ts)
X = sqrt(3)*Ubeta*Ts/Ud;
Y = (sqrt(3)/2*Ualpha-Ubeta/2)*sqrt(3)*Ts/Ud;
Z = (-sqrt(3)/2*Ualpha-Ubeta/2)*sqrt(3)*Ts/Ud;
end
向量作用时间计算函数:
function [Tx,Ty] = fcn(N,X,Y,Z)
switch N
case 1
Tx = Y; Ty = X;
case 2
Tx = -Z; Ty = -Y;
case 3
Tx = X; Ty = Z;
case 4
Tx = -Y; Ty = -X;
case 5
Tx = Z; Ty = Y;
case 6
Tx = -X; Ty = -Z;
otherwise
Tx = 0; Ty = 0;
end
end
比较生成脉宽函数;
function [y1,y2,y3] = fcn(u,Tcm1,Tcm2,Tcm3)
if u>Tcm1
y1 = 1;
else
y1 = 0;
end
if u>Tcm2
y2 = 1;
else
y2 = 0;
end
if u>Tcm3
y3 = 1;
else
y3 = 0;
end
end
根据不同扇区组生成对应控制IGBT脉冲:
function [pa,pb,pc] = fcn(N,y1,y2,y3)
switch N
case 1
pa = y1;
pb = y2;
pc = y3;
case 2
pa = y2;
pb = y1;
pc = y3;
case 3
pa = y3;
pb = y1;
pc = y2;
case 4
pa = y3;
pb = y2;
pc = y1;
case 5
pa = y2;
pb = y3;
pc = y1;
case 6
pa = y1;
pb = y3;
pc = y2;
otherwise
pa=0;pb=0;pc=0;
end
end
这个脉冲再添加各自对应的互补脉冲就形成了最终的控制脉冲(共六个)。
结果
拟模拟50HZ正弦合成矢量,幅度220sqrt(2),直流电源1000v,这个电源大小一定要大到能够合成旋转矢量,小了合成不了!仿真时间0.1s。

FFT分析:
这个工具箱在powergui里找。数据需要先设置示波器让其导出数据到工作空间。

看到这可能大家会说,你这个不行啊,总谐失真都大于1了,其实吧,svpwm是针对电机磁链等效来推的算法,这个电压波形是做不到与正弦差不多的,spwm的THD也比它小一点,想看效果得拿它做电机仿真。下面先看一下负载电流。
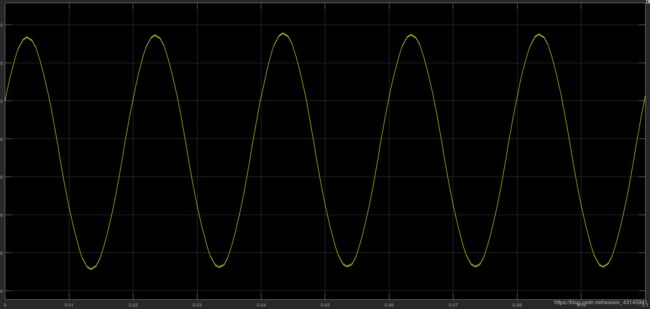
这个电流非常接近正弦,效果还是不错的。
电机仿真:
(p=2,功率2200VA,额定电压380V,额定频率50HZ,定子电阻0.435欧,定子电感0.002H,转子电阻0.816欧,转子电感0.002H,互感0.069H,负载转矩T = 0)
转速图就不上了,本人感觉仅次于矢量控制了,我们看磁链图:
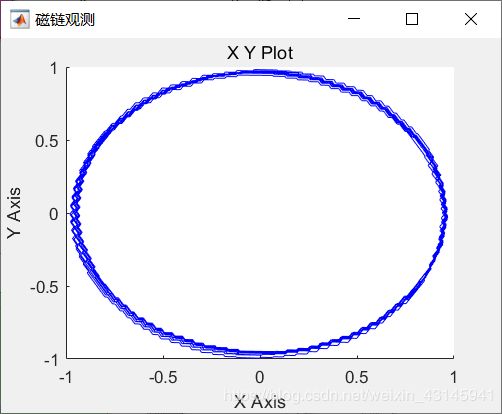
一个规规矩矩的圆,和加正弦波得到的结果一样,我再上一张spwm控制相同异步电机的磁链图:
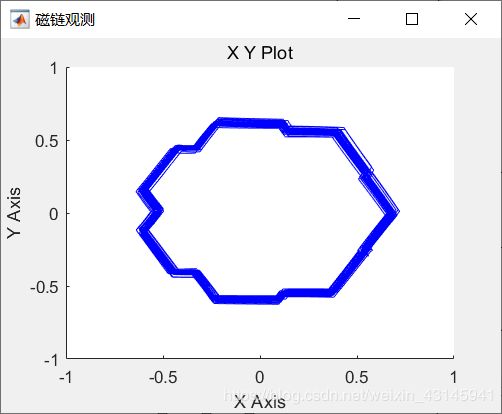
看到差距了吧,而且这个spwm如果负载直接接电感出来的电流也是很正弦的,但是放在电机上就模拟不出圆磁动势了,这是因为你直接加电感没有考虑空间位置,而电机的电感还有空间相位关系,而这恰恰是svpwm考虑了的。
