用户存续期价值评估CLV(三) Gamma-Gamma模型 Python模拟

Gamma-Gamma模型

前面已经提到过，Pareto/NBD和BG/NBD模型只对客户存续时间和交易次数进行建模，并不涉及客户未来交易所带来的现金价值。
Gamma-Gamma模型就是对这个问题的一个扩展解决方案。

Gamma-Gamma模型做了如下假设：

• 从客户角度上来说，交易金额在每个客户的平均交易价值上随机波动。(这一点并不是很有说服力)
• 所观察到的交易价值均值是隐含价值均值 () 的非完美计量
• 交易价值均值在客户中是变化的，即使这个值是稳定的（这个假设非常大)
• 在客户中的平均交易价值的分布与交易过程无关。换句话说，就是现金价值与客户购买次数和客户存续时间可以分开建模。 (在真实场景下，这个假设很可能不成立)

如果我们令 $z_1,z_2,...,z_x$ 为客户历史上的每次交易的价值序列，所观测到的历史交易价值均值为 $\bar{z}={\sum }_{i=1}^x{z}_i/x$

模型认为：

• $z_i$ 服从 $gamma(p,v)$分布，根据Gamma分布的可加性，在 $x$ 个交易的总价值的分布服从 $gamma(px,v)$ ; 而根据gamma分布的尺度特性，$\bar{z}$ 服从 $gamma(px,vx)$
• $v$ 服从 $gamma(q,\gamma )$

模型的条件期望为：
$E(M|p,q,\gamma ,m_x,x)=\frac{(\gamma +m_{x}x)p}{px+q-1}=(\frac{q-1}{px+q-1})\frac{\gamma p}{q-1}+(\frac{px}{px+q-1})m_x$
$m_x$是观测的交易价值均值
可采用最大似然估计来估算参数

采用lifetimes包中包含经济价值的数据来拟合模型

from lifetimes.datasets import load_cdnow_summary_data_with_monetary_value

summary_with_money_value = load_cdnow_summary_data_with_monetary_value()
summary_with_money_value.head()
returning_customers_summary = summary_with_money_value[summary_with_money_value['frequency']>0]

print(returning_customers_summary.head())

上面的monetary_value就是价值均值

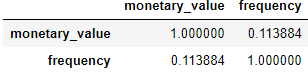
returning_customers_summary[['monetary_value', 'frequency']].corr()

检查价值均值和交易频率的皮尔森相关系数：相关性接近0

from lifetimes import GammaGammaFitter

ggf = GammaGammaFitter(penalizer_coef = 0)
ggf.fit(returning_customers_summary['frequency'],
        returning_customers_summary['monetary_value'])
print(ggf)

print(ggf.conditional_expected_average_profit(
        summary_with_money_value['frequency'],
        summary_with_money_value['monetary_value']
    ).head(10))

print("Expected conditional average profit: %s, Average profit: %s" % (
    ggf.conditional_expected_average_profit(
        summary_with_money_value['frequency'],
        summary_with_money_value['monetary_value']
    ).mean(),
    summary_with_money_value[summary_with_money_value['frequency']>0]['monetary_value'].mean()
))

训练Gamma-Gamma模型，并预测平均交易价值

from lifetimes.datasets import load_cdnow_summary
from lifetimes import BetaGeoFitter
data = load_cdnow_summary(index_col=[0])
bgf = BetaGeoFitter(penalizer_coef=0.0)
bgf.fit(data['frequency'], data['recency'], data['T'])

bgf.fit(summary_with_money_value['frequency'], summary_with_money_value['recency'], summary_with_money_value['T'])

print(ggf.customer_lifetime_value(
    bgf, #the model to use to predict the number of future transactions
    summary_with_money_value['frequency'],
    summary_with_money_value['recency'],
    summary_with_money_value['T'],
    summary_with_money_value['monetary_value'],
    time=12, # months
    discount_rate=0.01 # monthly discount rate ~ 12.7% annually
).head(10))

采用DCF(Discount Cash Flow)计算CLV