总结
集训第一次NOIP模拟考试,有得也有失

第一题是之前做过的原题,这次没有写出来,交了一个爆搜,不应该
第二题全场只有lsx大佬过了,考试的原数据能贪心过掉80分运气还不错
第三题是题库的原题,但是之前没有做,打表得到了50分
第四题比较水,用线段树维护一个区间最大值就可以
A、信息传递
分析
题目实际上就是让你求有向图中的最小环,这样的算法就很多了
60分爆搜(考场代码)
把每一个点都枚举一遍
还有更优的爆搜可以过掉这道题
#include
using namespace std;
const int maxn=200005;
struct asd{
int from,to,next;
}b[maxn];
int head[maxn];
int tot=1;
void ad(int aa,int bb){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
head[aa]=tot++;
}
int n,now,xz;
int vis[maxn];
void dfs(int xx,int cnt){
if(now) return;
for(int i=head[xx];i!=-1;i=b[i].next){
int u=b[i].to;
if(!vis[u]){
if(u==xz){
now=cnt+1;
return;
}
vis[u]=1;
dfs(u,++cnt);
}
}
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d",&n);
for(int i=1;i<=n;i++){
int aa;
scanf("%d",&aa);
ad(i,aa);
}
int ans=0x3f3f3f3f;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
xz=i;
now=0;
dfs(i,0);
if(now==0) continue;
ans=min(ans,now);
}
printf("%d\n",ans);
return 0;
}
Tarjan求强连通分量缩点
因为每一个点的出度只能为一,所以有向图中不会出现环套环的情况
因此强连通分量只能是一个环
我们只要找出大小最小的那一个强连通分量就可以了
#include
using namespace std;
const int maxn=200005;
struct asd{
int from,to,next;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
head[aa]=tot++;
}
int shuyu[maxn],siz[maxn];
int dfn[maxn],low[maxn],dfnc,sta[maxn],top,js;
void tar(int xx){
dfn[xx]=low[xx]=++dfnc;
sta[++top]=xx;
for(int i=head[xx];i!=-1;i=b[i].next){
int u=b[i].to;
if(!dfn[u]){
tar(u);
low[xx]=min(low[xx],low[u]);
} else if(!shuyu[u]){
low[xx]=min(low[xx],dfn[u]);
}
}
if(dfn[xx]==low[xx]){
js++;
while(1){
int now=sta[top--];
shuyu[now]=js;
siz[js]++;
if(xx==now) break;
}
}
}
int main(){
memset(head,-1,sizeof(head));
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
int aa;
scanf("%d",&aa);
ad(i,aa);
}
for(int i=1;i<=n;i++){
if(!dfn[i]) tar(i);
}
int mmin=0x3f3f3f3f;
for(int i=1;i<=js;i++){
if(siz[i]==1) continue;
mmin=min(mmin,siz[i]);
}
printf("%d\n",mmin);
return 0;
}
加权并查集求最小环
如果A可以将信息传递给B,那么将A和B并在一起,更新A和B到祖先节点的距离
如果有两个点祖先节点相同,那么就可以构成一个环,长度为两个点到祖先节点长度之和+1
#include
#include
#include
#include
using namespace std;
const int maxn=200010;
int fa[maxn],du[maxn];
int ans;
int zhao(int x){
if(x==fa[x]) return fa[x];
int last=fa[x];
fa[x]=zhao(fa[x]);
du[x]+=du[last];
return fa[x];
}
void bing(int x,int y){
if(zhao(x)==zhao(y)){
ans=min(ans,du[x]+du[y]+1);
} else {
fa[zhao(x)]=zhao(y);
du[x]=du[y]+1;
}
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
fa[i]=i;
}
ans=0x3f3f3f3f;
for(int i=1;i<=n;i++){
int xx;
scanf("%d",&xx);
bing(i,xx);
}
printf("%d\n",ans);
return 0;
}
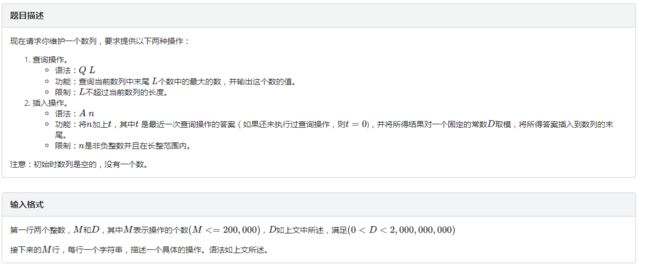
B. 传染病控制
分析
考试时一直以为是一道考察思维量的题目,在想比较优秀的代码
树形DP or 贪心
看了题解后,发现是一个暴力枚举,而且也不太好写
80分贪心(考试代码)
当时写贪心的时候没有想到能水这么多分
思路肯定是不正确的,但是能水过大多数情况
#include
using namespace std;
const int maxn=10005;
struct asd{
int from,to,next;
}b[maxn];
int head[maxn];
int tot=1;
void ad(int aa,int bb){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
head[aa]=tot++;
}
int n,p;
int f[maxn];
int dep[maxn],siz[maxn],sizz[maxn],maxd;
void dfs(int now,int fa){
dep[now]=dep[fa]+1;
siz[now]=1;
f[now]=fa;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==fa) continue;
sizz[now]++;
dfs(u,now);
siz[now]+=siz[u];
}
}
bool vis[maxn];
void dfs2(int now,int fa){
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==fa) continue;
dfs2(u,now);
}
}
vector g[maxn];
int du;
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&p);
for(int i=1;i<=p;i++){
int aa,bb;
scanf("%d%d",&aa,&bb);
ad(aa,bb);
ad(bb,aa);
if(aa==1 || bb==1) du++;
}
if(du==1 || du==n-1){
printf("%d\n",du);
return 0;
}
dfs(1,0);
int ans=0;
for(int i=1;i<=n;i++){
maxd=max(dep[i],maxd);
}
for(int i=2;i<=maxd;i++){
int ll=-1,jl=0;
for(int j=2;j<=n;j++){
if(vis[j]) continue;
if(dep[j]==i){
if(sizz[j]>ll || (sizz[j]>=ll && siz[j]>siz[jl])){
ll=sizz[j];
jl=j;
}
}
}
if(jl==0) continue;
ans+=siz[jl];
dfs2(jl,f[jl]);
}
printf("%d\n",n-ans);
return 0;
}
100分爆搜代码
#include
using namespace std;
const int maxn=1005;
struct asd{
int from,to,next;
}b[maxn];
int head[maxn];
int tot=1;
void ad(int aa,int bb){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
head[aa]=tot++;
}
int n,p;
int f[maxn];
int dep[maxn],maxd;
void dfs(int now,int fa){
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==fa) continue;
dep[u]=dep[now]+1;
f[u]=now;
maxd=max(maxd,dep[u]);
dfs(u,now);
}
}//预处理出每一个节点的深度和它的父亲
int cut[maxn];
void dfs2(int now,int col){
cut[now]=col;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(u==f[now]) continue;
cut[u]=col;
dfs2(u,col);
}
}//把整个子树数染色,标记成已经安全隔离
int cnt[maxn],dep2[maxn][maxn];
int js(int now){
int sum=0;
for(int i=1;i<=cnt[now];i++){
if(cut[dep2[now][i]]==0){
sum++;
}
}
return sum;
}//统计每一个深度中未被安全隔离的人数
int ans=0x3f3f3f3f;
void solve(int now,int sum){
if(sum>=ans) return;//剪枝优化
if(now>maxd || js(now)==0){
ans=min(ans,sum);
return;
}//到达边界
for(int i=1;i<=cnt[now];i++){
int to=dep2[now][i];//枚举当前深度所有节点
if(cut[to]==1) continue;//如果当前节点已被隔离,就不用再遍历
dfs2(to,1);//否则标记已经安全隔离
solve(now+1,sum+js(now));//计算答案
dfs2(to,0);//还原,枚举另一种情况
}
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&p);
for(int i=1;i<=p;i++){
int aa,bb;
scanf("%d%d",&aa,&bb);
ad(aa,bb);
ad(bb,aa);
}
dfs(1,0);
for(int i=1;i<=n;i++){
dep2[dep[i]][++cnt[dep[i]]]=i;
}
solve(1,1);
printf("%d\n",ans);
return 0;
}
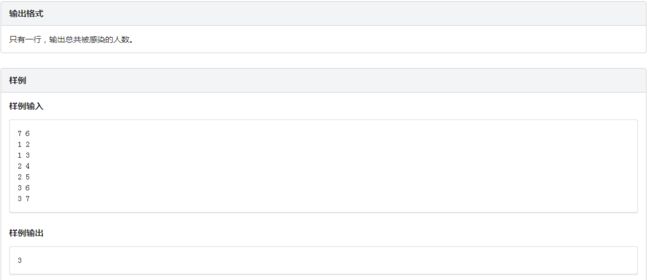
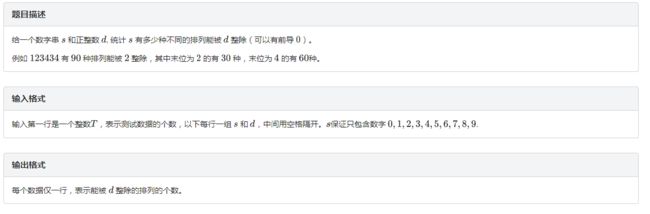
C、排列
50分打表(考场代码)
#include
using namespace std;
typedef long long ll;
const int maxn=4e6+5;
ll ans;
map mp;
int main(){
int t;
scanf("%d",&t);
while(t--){
mp.clear();
ans=0;
char s[50];
ll xx;
scanf("%s",s);
scanf("%lld",&xx);
int len=strlen(s);
if(len==1){
ll now=s[0]-'0';
if(now%xx==0) printf("1\n");
else printf("0\n");
} else if(len==2){
for(int i=0;i<=1;i++){
for(int j=0;j<=1;j++){
if(j==i) continue;
ll now=(s[i]-'0')*10ll+(s[j]-'0');
if(mp[now]==1) continue;
mp[now]=1;
if(now%xx==0) ans++;
}
}
printf("%lld\n",ans);
} else if(len==3){
for(int i=0;i 100分STL
STL中有一个自动求全排列的函数\(next \_ permutation\)
所以代码就很简洁了
#include
using namespace std;
typedef long long ll;
ll a[15],t;
char s[15];
int main(){
scanf("%lld",&t);
while(t--){
ll now;
scanf("%s%lld",s,&now);
ll len=strlen(s);
for(int i=1;i<=len;i++){
a[i]=s[i-1]-'0';
}
sort(a+1,a+1+len);
ll ans=0;
while(1){
ll tot=0;
for(int i=1;i<=len;i++){
tot=tot*10+a[i];
}
if(tot%now==0) ans++;
if(next_permutation(a+1,a+len+1)==0) break;
}
printf("%lld\n",ans);
}
return 0;
}
D、最大数
分析
显然用线段树维护一个区间最值
57分暴力(对拍用)
#include
using namespace std;
typedef long long ll;
int cnt=0;
const int maxn=2e5+5;
ll lat;
ll a[maxn];
int main(){
int m;
ll d;
scanf("%d%lld",&m,&d);
for(int i=1;i<=m;i++){
char ch;
ll now;
scanf(" %c %lld",&ch,&now);
if(ch=='A'){
a[++cnt]=(lat+now)%d;
} else {
ll mmax=0;
for(int j=cnt;j>cnt-now;j--){
mmax=max(mmax,a[j]);
}
lat=mmax;
printf("%lld\n",mmax);
}
}
}
100分代码(线段树)
#include
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
struct trr{
ll l,r,w;
}tr[maxn];
ll m,mod,las;
void push_up(ll da){
tr[da].w=max(tr[da<<1].w,tr[da<<1|1].w);
}
void build(ll da,ll s,ll t){
tr[da].l=s;
tr[da].r=t;
if(s==t){
tr[da].w=0;
return;
}
int mids=(s+t)>>1;
build(da<<1,s,mids);
build(da<<1|1,mids+1,t);
push_up(da);
}
void xg(ll da,ll gg,ll ww){
if(tr[da].l==tr[da].r){
tr[da].w=ww;
return;
}
ll mids=(tr[da].l+tr[da].r)>>1;
if(gg<=mids) xg(da<<1,gg,ww);
else xg(da<<1|1,gg,ww);
push_up(da);
}
ll cx(ll da,ll s,ll t){
if(tr[da].l>=s && tr[da].r<=t){
return tr[da].w%mod;
}
ll ans=0;
ll mids=(tr[da].l+tr[da].r)>>1;
if(s<=mids) ans=max(ans,cx(da<<1,s,t));
if(t>mids) ans=max(ans,cx(da<<1|1,s,t));
return ans%mod;
}
ll cnt=0;
int main(){
scanf("%lld%lld",&m,&mod);
build(1,1,m);
for(ll i=1;i<=m;i++){
char ch;
ll now;
scanf(" %c %lld",&ch,&now);
if(ch=='A'){
xg(1,++cnt,(now+las)%mod);
} else {
las=cx(1,cnt-now+1,cnt);
printf("%lld\n",las);
}
}
return 0;
}