最大熵马尔科夫模型(MEMM)
最大熵马尔科夫模型
Maximum Entropy Markov Models (MEMM)
引入和定义
隐马尔科夫模型作了两个基本假设:
(1)齐次马尔科夫假设,即假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关:
P ( i t ∣ i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , 3 , ⋯ , T P(i_{t}|i_{t-1},o_{t-1},\cdots,i_{1},o_{1}) = P(i_{t}|i_{t-1}),t = 1, 2,3,\cdots,T P(it∣it−1,ot−1,⋯,i1,o1)=P(it∣it−1),t=1,2,3,⋯,T (2)观测独立假设,即假设任意时刻的观测值依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关:
P ( o t ∣ i T , o T , i T − 1 , o T − 1 , ⋯ , i t + 1 , o t + 1 , i t , i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( o t ∣ i t ) , t = 1 , 2 , 3 , ⋯ , T P(o_{t}|i_{T},o_{T},i_{T-1},o_{T-1},\cdots,i_{t+1},o_{t+1},i_{t},i_{t-1},o_{t-1},\cdots,i_{1},o_{1}) = P(o_{t}|i_{t}),t = 1, 2,3,\cdots,T P(ot∣iT,oT,iT−1,oT−1,⋯,it+1,ot+1,it,it−1,ot−1,⋯,i1,o1)=P(ot∣it),t=1,2,3,⋯,T
而这两个假设就体现出了隐马尔科夫模型的不足:
(1)许多任务受益于更丰富的观察表示,数据集的形式非常的丰富,比如在文本相关的任务中,“首字母是否大写并且不在开头”可以作为判断一个单词是否是人名,公司名的依据之一 (比如Apple苹果公司和aplle苹果)。这是HMM所做不到的。也就是说,HMM的特征表示有限,不能表示交叉(overlapping)的特征。并且,隐马尔科夫模型中假设特征之间是相互独立的,它们之间很大可能存在相关性。
(2)设置隐马尔可夫(HMM)参数来最大化观测序列的可能性。然而,在大多数文本应用中,任务都是预测给定观察序列的状态序列。换句话说,HMM中使用的是联合概率P(X, Y),而很多时候我们使用的是条件概率P(X| Y)。也就是说,HMM通过联合概率解决条件概率的问题,这是不合适的。
为了解决HMM的不足,我们将采用最大熵马尔科夫模型(MEMM)来解决HMM的不足。
最大熵马尔科夫模型
HMM中有两个概率函数
状态转移概率函数和状态观测概率函数:
状态转移概率函数: P ( s ∣ s ′ ) P(s|s') P(s∣s′)状态观测概率函数: P ( o ∣ s ) P(o|s) P(o∣s)
而在MEMM中只用了一个概率函数代替了HMM中的两个概率函数: P ( s ∣ s ′ , o ) P(s|s',o) P(s∣s′,o)

在HMM中下一个状态的概率递归公式:
α t + 1 ( s ) = ∑ s ′ ∈ S α t ( s ′ ) ⋅ P ( s ∣ s ′ ) ⋅ P ( o t + 1 ∣ s ) \alpha_{t+1}(s) = \sum_{s'\in S} \alpha_{t}(s') \cdot P(s|s') \cdot P(o_{t+1}|s) αt+1(s)=s′∈S∑αt(s′)⋅P(s∣s′)⋅P(ot+1∣s)
在MEMM中下一个状态的概率递归公式:
α t + 1 ( s ) = ∑ s ′ ∈ S α t ( s ′ ) ⋅ P s ′ ( s ∣ o t + 1 ) \alpha_{t+1}(s) = \sum_{s'\in S} \alpha_{t}(s') \cdot P_{s'}(s|o_{t+1}) αt+1(s)=s′∈S∑αt(s′)⋅Ps′(s∣ot+1)其中 P s ‘ ( s ∣ o ) = P ( s ∣ s ′ , o ) P_{s^{`}}(s|o)=P(s|s', o) Ps‘(s∣o)=P(s∣s′,o)
给定一个状态 s t s_{t} st和当前状态的观测值 o t + 1 o_{t+1} ot+1,预测当前状态 s t + 1 s_{t+1} st+1的概率。下图展示了计算状态、标签、标记转换的不同之处。(上半部分是HMM,下半部分是MEMM)

最大熵
最大熵是一个根据数据估计概率分布的一个框架。
最大似然函数就具有如下分布: P s ′ ( s ∣ o ) = 1 Z ( o , s ′ ) e x p ( ∑ a λ a ⋅ f a ( o , s ) ) P_{s'}(s|o) = \frac{1}{Z(o,s')}exp(\sum_{a}\lambda_{a} \cdot f_{a}(o,s)) Ps′(s∣o)=Z(o,s′)1exp(a∑λa⋅fa(o,s))其中, a = < b , s > a=
由于 ∑ y P ( y ∣ x ) = 1 \sum_{y}P(y|x)=1 ∑yP(y∣x)=1,得
P w ( y ∣ x ) = 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) P_{w}(y|x)=\frac{1}{Z_{w}(x)}exp(\sum_{i=1}^{n}w_{i}f_{i}(x,y)) Pw(y∣x)=Zw(x)1exp(i=1∑nwifi(x,y))
其中,
Z w ( x ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) Z_{w}(x) = \sum_{y}exp(\sum_{i=1}^{n}w_{i}f_{i}(x,y)) Zw(x)=y∑exp(i=1∑nwifi(x,y))关键在于,在MEMM中,是对局部的随机变量之间的特征建立条件概率函数,最终按照HMM的思想进行求解
HMM中计算P(Y|X)的表达式:
对固定的状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I=(i_{1},i_{2},\cdots,i_{T}) I=(i1,i2,⋯,iT),观测序列 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_{1},o_{2 },\cdots,o_{T}) O=(o1,o2,⋯,oT)的概率是 P ( O ∣ I , λ ) P(O|I,\lambda) P(O∣I,λ), P ( O ∣ I , λ ) = b i 1 ( o 1 ) b i 2 ( o 2 ) ⋯ b i T ( o T ) P(O|I,\lambda)=b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})\cdots b_{i_{T}}(o_{T}) P(O∣I,λ)=bi1(o1)bi2(o2)⋯biT(oT)MEMM中计算P(Y|X)的表达式 :
P ( y 1 : n ∣ x 1 : n ) = ∏ i = 1 n P ( y i ∣ y i − 1 , x 1 : n ) = ∏ i = 1 n e x p ( w T f ( y i , y i − 1 , x 1 : n ) ) Z ( y i − 1 , x 1 : n ) P(y_{1:n}|x_{1:n}) = \prod_{i=1}^{n}P(y_{i}|y_{i-1},x_{1:n}) = \prod_{i=1}^{n}\frac{exp(w^{T}f(y_{i},y_{i-1},x_{1:n}))}{Z(y_{i-1},x_{1:n})} P(y1:n∣x1:n)=i=1∏nP(yi∣yi−1,x1:n)=i=1∏nZ(yi−1,x1:n)exp(wTf(yi,yi−1,x1:n))注意到其中的归一化函数是在乘积式子内并且每一个乘积式子就是一个最大熵模型的表示,即MEMM是将原本的HMM中的表达式替换为一个个最大熵模型
MEMM存在的问题:标注偏置(label bias problem)
由于上述的归一化函数是在乘积式子内,因此就存在以下的标注偏置问题:当某个状态A对应的特征M出现过多时,任何一个状态都会倾向去转移到状态A,即 P ( y a ∣ y ? , x ? ) > = P ( y ? ∣ y ? , x ? ) P(y_{a}|y_{?},x_{?})>=P(y_{?}|y_{?},x_{?}) P(ya∣y?,x?)>=P(y?∣y?,x?),当使用viterbi算法时,由于其取最大化,就会导致如下图所示的标注偏置:
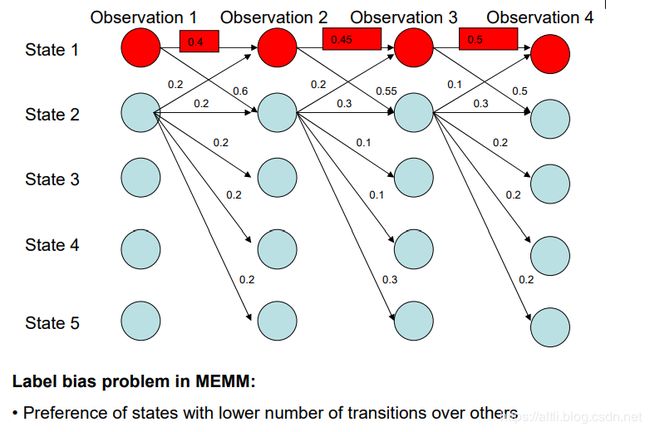
为了解决MEMM等模型出现的标注偏置问题,并保留MEMM的诸多优点,条件随机场(CRF)被提出。