机器学习十大经典算法之线性回归(学习笔记整理)
机器学习十大经典算法之线性回归(学习笔记整理)
- 一、一元线性回归
- 二、多元线性回归
- 三、回归模型的评估与诊断
- 1.模型和回归系数的显著性检验
- 2.正态性检验
- 3.多重共线性检验
- 4.线性相关性检验
- 5.残差独立性检验
- 6.方差齐性检验
- 7.异常值检验
一、一元线性回归
一元线性回归模型也称为简单线性回归模型,模型中只含有一个自变量,数学表达式 y = a + b x + ε y=a+bx+\varepsilon y=a+bx+ε其中a、b为回归系数, ε \varepsilon ε为模型的误差项。要得到理想的拟合线,则要使误差 ε \varepsilon ε总体上最小,于是转换成了误差平方和最小的问题,此方法就是“最小二乘法”。
回归系数的推导过程:
J ( a , b ) = ∑ i = 1 n ε 2 = ∑ i = 1 n ( y i − ( a + b x i ) ) 2 J(a,b) = \sum_{i=1}^{n}{\varepsilon^2} = \sum_{i=1}^{n}{(y_i-(a+bx_i))^2} J(a,b)=i=1∑nε2=i=1∑n(yi−(a+bxi))2 ⇒ J ( a , b ) = ∑ i = 1 n ( y i 2 + a 2 + b 2 x i 2 + 2 a b x i − 2 a y i − 2 b x i y i ) \Rightarrow J(a,b) = \sum_{i=1}^{n}{(y_i^2+a^2+b^2x_i^2+2abx_i-2ay_i-2bx_iy_i)} ⇒J(a,b)=i=1∑n(yi2+a2+b2xi2+2abxi−2ayi−2bxiyi) 令 { ∂ J ∂ a = ∑ i = 1 n ( 0 + 2 a + 0 + 2 b x i − 2 y i + 0 ) = 0 ∂ J ∂ b = ∑ i = 1 n ( 0 + 0 + 2 b x i 2 + 2 a x i + 0 − 2 x i y i ) = 0 令 \begin{cases} \dfrac{\partial J}{\partial a}=\sum_{i=1}^{n}{(0+2a+0+2bx_i-2y_i+0)=0} \\[2ex] \dfrac{\partial J}{\partial b}=\sum_{i=1}^{n}{(0+0+2bx_i^2+2ax_i+0-2x_iy_i)=0}\\ \end{cases} 令⎩⎪⎪⎨⎪⎪⎧∂a∂J=∑i=1n(0+2a+0+2bxi−2yi+0)=0∂b∂J=∑i=1n(0+0+2bxi2+2axi+0−2xiyi)=0 ⇒ { a = y ‾ − b x ‾ b = ∑ x i y i − 1 n ∑ x i ∑ y i ∑ x i 2 − 1 n ( ∑ x i ) 2 \Rightarrow\begin{cases} a=\overline y-b\overline x\\[2ex] b=\dfrac{\sum x_iy_i-\frac{1}{n}\sum x_i\sum y_i}{\sum x_i^2-\frac{1}{n}(\sum x_i)^2}\\ \end{cases} ⇒⎩⎪⎪⎨⎪⎪⎧a=y−bxb=∑xi2−n1(∑xi)2∑xiyi−n1∑xi∑yi
Python中statsmodels模块下的ols函数可以实现线性回归的参数求解。
ols(formula,data,subset=None,drop_cols=None)
• formula:指定线性回归模型的公式,如’y~x+z’
• data:用于建模的数据集
• subset:通过bool类型的数组对象,获取data的子集用于建模
• drop_cols:指定data从要删除的变量
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
data=pd.read_csv(r'C:\Users\sc\Desktop\Salary_Data.csv')
sns.lmplot(x='YearsExperience',y='Salary',data=data,ci=None) #画带回归线的散点图
plt.show()
fit=sm.formula.ols('Salary~YearsExperience',data=data).fit() #构建回归模型
print(fit.summary()) #模型摘要,跟SPSS输出结果类似
二、多元线性回归
多元线性回归模型
( y 1 y 2 ⋮ y n ) n × 1 = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n p ) n × p ( β 1 β 2 ⋮ β p ) p × 1 + ( ε 1 ε 2 ⋮ ε n ) n × 1 \begin{pmatrix} y_1 \\ y_2 \\\vdots\\y_n \end{pmatrix} _{n\times1}= \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \\ \end{pmatrix}_{n\times p}\begin{pmatrix} \beta_1 \\ \beta_2 \\\vdots\\\beta_p \end{pmatrix} _{p\times1}+\begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\\vdots\\\varepsilon_n \end{pmatrix} _{n\times1} ⎝⎜⎜⎜⎛y1y2⋮yn⎠⎟⎟⎟⎞n×1=⎝⎜⎜⎜⎛x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1px2p⋮xnp⎠⎟⎟⎟⎞n×p⎝⎜⎜⎜⎛β1β2⋮βp⎠⎟⎟⎟⎞p×1+⎝⎜⎜⎜⎛ε1ε2⋮εn⎠⎟⎟⎟⎞n×1自变量个数为p,观测值个数为n,也可以简化表示为 y = X β + ε y=X\beta+\varepsilon y=Xβ+ε β \beta β为偏回归系数向量, ε \varepsilon ε为误差向量。
回归系数的推导过程:
J ( β ) = ∑ ε 2 = ∑ ( y − X β ) 2 J(\beta)=\sum\varepsilon^2=\sum (y-X\beta)^2 J(β)=∑ε2=∑(y−Xβ)2 ⇒ J ( β ) = ( y − X β ) T ( y − X β ) = ( y T − β T X T ) ( y − X β ) = ( y T y − y T X β − β T X T y + β T X T X β ) \Rightarrow J(\beta)=(y-X\beta)^T(y-X\beta)\\ \text {\qquad\qquad\;\,}=(y^T-\beta^TX^T)(y-X\beta)\\ \text {\qquad\qquad\qquad\qquad\qquad\;\;\,}=(y^Ty-y^TX\beta-\beta^TX^Ty+\beta^TX^TX\beta) ⇒J(β)=(y−Xβ)T(y−Xβ)=(yT−βTXT)(y−Xβ)=(yTy−yTXβ−βTXTy+βTXTXβ)
令 ∂ J ( β ) ∂ β = ( 0 − X T y − X T y + 2 X T X β ) = 0 令\dfrac{\partial J(\beta)}{\partial \beta}=(0-X^Ty-X^Ty+2X^TX\beta)=0 令∂β∂J(β)=(0−XTy−XTy+2XTXβ)=0 ⇒ X T y = X T X β \Rightarrow X^Ty=X^TX\beta ⇒XTy=XTXβ ⇒ β = ( X T X ) − 1 X T y \text {\quad\;\;\;\;\;\;\,}\Rightarrow \text {\;\;\;\;\;} \beta=(X^TX)^{-1}X^Ty ⇒β=(XTX)−1XTy用结果来看,要能求得偏回归系数, X T X X^TX XTX必须可逆,由于 ∣ X T X ∣ |X^TX| ∣XTX∣= ∣ X T ∣ ∣ X ∣ |X^T||X| ∣XT∣∣X∣= ∣ X ∣ 2 |X|^2 ∣X∣2,所以自变量 X X X不能线性相关,否则 ∣ X ∣ |X| ∣X∣=0会导致 X T X X^TX XTX不可逆。( X − 1 = A ∗ ∣ A ∣ X^{-1}=\dfrac{A^*}{|A|} X−1=∣A∣A∗, A ∗ A^* A∗是 A A A的伴随矩阵)
Python代码
import pandas as pd
from sklearn import model_selection
from statsmodels.api import formula as smf
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#拆分训练集和测试集
train,test=model_selection.train_test_split(data,test_size=0.2,random_state=1234)
#建模
#非数值型变量State处理成哑变量,套在C()中表示将其当做分类(Category)处理
model=smf.ols('Profit~RD_Spend+Administration+Marketing_Spend+C(State)',data=train).fit()
print('偏回归系数:',model.params)
print('模型摘要:',model.summary())
#删除test数据集中的因变量,用剩下的自变量进行预测
test_X=test.drop('Profit',axis=1)
pred=model.predict(test_X)
print('对比预测值和实际值:\n',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))
其中非数值型变量要处理成哑变量,还有一种通用的哑变量处理方法:
#生成哑变量
dummies=pd.get_dummies(data.State)
#将哑变量与原始数据集水平合并
data_new=pd.concat([data,dummies],axis=1)
#删除原变量和对照组
data_new.drop(['State','New York'],axis=1,inplace=True)
哑变量会有一个参照组,其他组的偏回归系数表示的是xx组相对于参照组xx怎样变化,是参照组的xx倍。
三、回归模型的评估与诊断
线性回归模型建立后需要对模型进行评估与诊断,线性回归模型有一些假设前提:
- 误差项 ε \varepsilon ε服从正态分布
- 不存在多重共线性
- 自变量与因变量线性相关
- 误差项 ε \varepsilon ε的独立性
- 方差齐性
另外线性回归模型对异常值是非常敏感的。
1.模型和回归系数的显著性检验
(1)模型的显著性检验-F检验
统计量
F = R S S / p E S S ( n − p − 1 ) \text{\qquad\qquad\qquad\qquad\qquad\qquad} F=\dfrac{RSS/p}{ESS(n-p-1)} F=ESS(n−p−1)RSS/p ~ F ( p , n − p − 1 ) F(p,n-p-1) F(p,n−p−1)
其中误差平方和ESS= ∑ i = 1 n ( y i − y ^ i ) 2 \sum_{i=1}^{n}{(y_i-\hat y_i)^2} ∑i=1n(yi−y^i)2,回归离差平方和RSS= ∑ i = 1 n ( y ^ i − y ‾ ) 2 \sum_{i=1}^{n}{(\hat y_i-\overline y)^2} ∑i=1n(y^i−y)2,有p个自变量,n个观测值。
PS:总离差平方和TSS= ∑ i = 1 n ( y i − y ‾ ) 2 \sum_{i=1}^{n}{(y_i-\overline y)^2} ∑i=1n(yi−y)2,三个离差平方和的关系是TSS=ESS+RSS,由于TSS固定不会随模型变化而变化,所以ESS和RSS存在严格的负向关系,由"最小二乘法",要使ESS最小,则RSS就要最大,所以F统计量越大越好。
假设
{ H 0 : β 0 = β 1 = ⋯ = β p = 0 H 1 : β 0 、 β 1 、 ⋯ 、 β p 不 全 为 0 \begin{cases} H_0:\beta_0=\beta_1=\cdots=\beta_p=0\\[2ex] H_1:\beta_0、\beta_1、\cdots、\beta_p不全为0\\ \end{cases} ⎩⎨⎧H0:β0=β1=⋯=βp=0H1:β0、β1、⋯、βp不全为0
(2)回归系数的显著性检验-t检验
统计量
t = β ^ j − β j S e ( β ^ j ) = β ^ j − β j c j j ∑ ε i 2 n − p − 1 \text{\qquad\qquad\qquad\qquad\qquad\quad} t=\dfrac{\hat\beta_j-\beta_j}{Se(\hat\beta_j)}=\dfrac{\hat\beta_j-\beta_j}{\sqrt{c_{jj}\dfrac{\sum\varepsilon_i^2}{n-p-1}}} t=Se(β^j)β^j−βj=cjjn−p−1∑εi2β^j−βj ~ t ( n − p − 1 ) t(n-p-1) t(n−p−1)
其中 β ^ j \hat\beta_j β^j为第j个系数的估计值; β j \beta_j βj为原假设的值即为0; S e ( β ^ j ) Se(\hat\beta_j) Se(β^j)为回归系数 β ^ j \hat\beta_j β^j的标准误, c j j c_{jj} cjj为矩阵 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1主对角线上第j个元素, ∑ ε i 2 \sum\varepsilon_i^2 ∑εi2为误差平方和。
假设
{ H 0 : β j = 0 , j = 1 , 2 , ⋯ , p H 1 : β j ≠ 0 \begin{cases} H_0:\beta_j=0,j=1,2,\cdots,p\\[2ex] H_1:\beta_j\neq0\\ \end{cases} ⎩⎨⎧H0:βj=0,j=1,2,⋯,pH1:βj̸=0

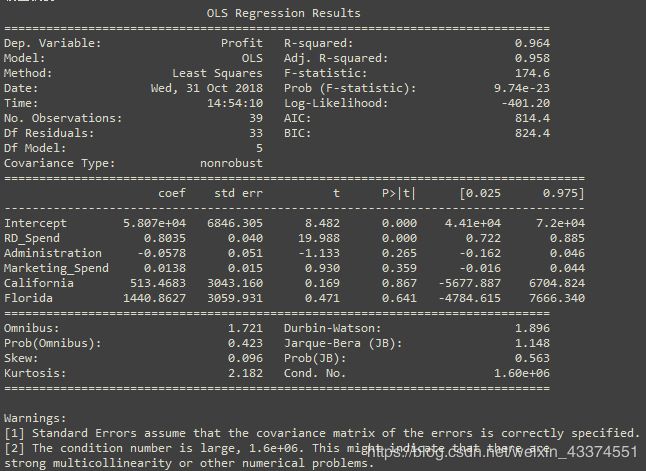
由模型摘要可以看到F统计量、t统计量的值和其对应的p值,如果p值小于显著性设定值0.05则拒绝原假设,说明模型或者系数是显著的。
2.正态性检验
由 y = X β + ε y=X\beta+\varepsilon y=Xβ+ε,因为 X X X是已知变量,所以要求 ε \varepsilon ε服从正态分布,实质就是要求因变量 y y y服从正态分布。正态性检验有两类方法,一是定性的图形法(直方图、PP图、QQ图),一是定量的非参数检验(Shapiro检验和K-S检验)。
(1)直方图法:
import pandas as pd
import scipy.stats as stats
import seaborn as sns
import matplotlib.pyplot as plt
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#设置中文和负号正常显示
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False
#绘制直方图
sns.distplot(a=data.Profit,bins=10,fit=stats.norm,norm_hist=True,
hist_kws={'color':'steelblue','edgecolor':'black'},
kde_kws={'color':'black','linestyle':'--','label':'核密度曲线'},
fit_kws={'color':'red','linestyle':':','label':'正态密度曲线'})
#显示图例
plt.legend()
plt.show()

核密度曲线和理论的正态密度曲线比较吻合,可以直观上认为因变量服从正态分布。
(2)PP图和QQ图:
PP图的思想是比对正态分布的累计概率值和实际分布的累计概率值;QQ图的思想是比对正态分布的分位数和实际分布的分位数。
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#设置中文和负号正常显示
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False
#残差的正态性检验
pp_qq_plot=sm.ProbPlot(data.Profit)
#绘制PP图
pp_qq_plot.ppplot(line='45')
plt.title('P-P图')
#绘制QQ图
pp_qq_plot.qqplot(line='q')
plt.title('Q-Q图')
plt.show()
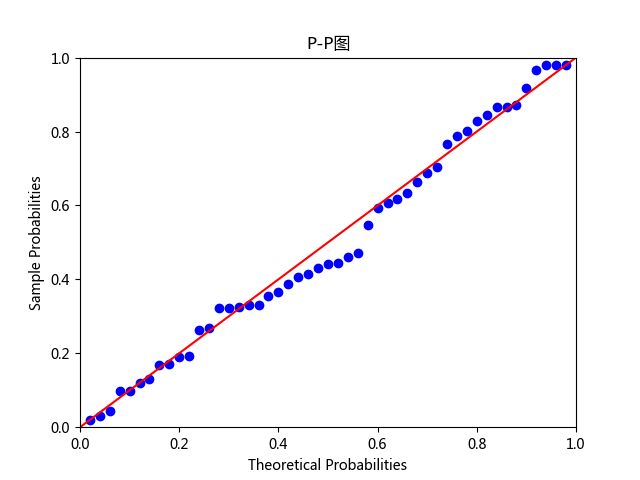
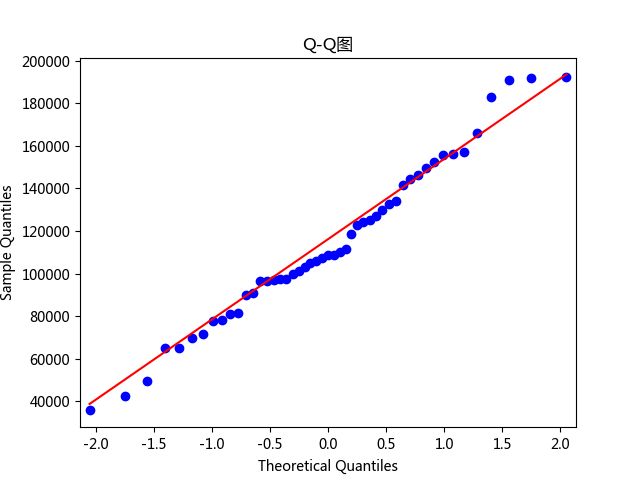
散点均落在直线附近,没有较大偏离,可以认为因变量近似服从正态分布。
(3)Shapiro检验和K-S检验:
这两种检验的原假设均为变量服从正态分布。数据量低于5000,使用Shapiro检验;数据量高于5000,使用K-S检验。
import pandas as pd
import scipy.stats as stats
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#Shapiro检验
print(stats.shapiro(data.Profit))
#K-S检验
print(stats.kstest(rvs=data.Profit,args=(data.Profit.mean(),data.Profit.std()),cdf='norm'))
![]()
两种检验的结果,第一项都是统计量的值,第二项都是p值。均大于0.05,接受原假设,服从正态分布。亲测K-S检验必须传入args(均值,标准差),否则结果是统计量为1,p值为0。
如果因变量不满足正态分布,则需要对其做某种数学变换,如 log ( y ) 、 y 、 1 y 、 1 y 、 y 2 、 1 y 2 \log(y)、\sqrt y、\frac{1}{\sqrt y}、\frac{1}{y}、y^2、\frac{1}{y^2} log(y)、y、y1、y1、y2、y21等。
3.多重共线性检验
多重共线性使用方差膨胀因子(Variance Inflation Factor,VIF)来检验,如果VIF>10,说明变量间存在多重共线性;如果VIF>100,说明变量间存在严重多重共线性。
V I F k = 1 1 − R k 2 VIF_k=\frac{1}{1-R_k^2} VIFk=1−Rk21构建第k个自变量与其余变量的线性组合 x k = c 0 + a 1 x 1 + ⋯ + a p x p + ε ( 右 边 不 含 x k ) x_k=c_{0}+a_1x_1+\cdots+a_px_p+\varepsilon(右边不含x_k) xk=c0+a1x1+⋯+apxp+ε(右边不含xk),可得到对应的可决系数 R k 2 R_k^2 Rk2。
import pandas as pd
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#自变量X(包含RD_Spend、Marketing_Spend和常数列1)
x=sm.add_constant(data.ix[:,['RD_Spend','Marketing_Spend']])
#构造DataFrame,存储VIF值
vif=pd.DataFrame()
vif['features']=x.columns
vif['VIF Factor']=[variance_inflation_factor(x.values,i) for i in range(x.shape[1])]
print(vif)
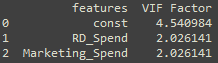
如果存在多重共线性,则可以考虑删除变量或重新选择模型(岭回归和LASSO回归)。
4.线性相关性检验
线性相关性可以直观的用散点图观察,也可以用Pearson相关系数检验。
ρ x y = C O V ( x , y ) D ( x ) D ( y ) \rho_{xy}=\frac{COV(x,y)}{\sqrt{D(x)}\sqrt{D(y)}} ρxy=D(x)D(y)COV(x,y)其中 C O V ( x , y ) COV(x,y) COV(x,y)是自变量x与因变量y的协方差, D ( x ) D(x) D(x)和 D ( y ) D(y) D(y)是各自的方差。
{ ∣ ρ ∣ ≥ 0.8 , 高 度 相 关 0.5 ≤ ∣ ρ ∣ < 0.8 , 中 度 相 关 0.3 ≤ ∣ ρ ∣ < 0.5 , 弱 相 关 ∣ ρ ∣ < 0.3 , 几 乎 不 相 关 \begin{cases} |\rho|\geq0.8,高度相关\\[2ex] 0.5\leq|\rho|<0.8,中度相关\\[2ex] 0.3\leq|\rho|<0.5,弱相关\\[2ex] |\rho|<0.3,几乎不相关\\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧∣ρ∣≥0.8,高度相关0.5≤∣ρ∣<0.8,中度相关0.3≤∣ρ∣<0.5,弱相关∣ρ∣<0.3,几乎不相关
import pandas as pd
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
#各个自变量与因变量的相关系数
print(data.drop('Profit',axis=1).corrwith(data.Profit))
5.残差独立性检验
残差的独立性检验一般使用Durbin_Watson统计量来检验,如果DW值在2左右,则表明残差项之间是不相关的。DW值在模型摘要里有。
6.方差齐性检验
方差齐性是指残差项的方差不随自变量的变动而呈现某种趋势。如果不满足方差齐性,则残差的趋势可以被自变量刻画,会导致偏回归系数不具备有效性。一般有两种方法检验方差齐性,一是图形法(散点图),二是统计检验法(BP检验)。
(1)图形法:
绘制残差与自变量之间的散点图
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.api import formula as smf
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
model=smf.ols('Profit~RD_Spend+Marketing_Spend',data=data).fit()
#设置第一张子图的位置
ax1=plt.subplot2grid(shape=(2,1),loc=(0,0))
#绘制散点图,使用的是标准化残差
ax1.scatter(data.RD_Spend,(model.resid-model.resid.mean())/model.resid.std())
#添加水平参考线
ax1.hlines(y=0,xmin=data.RD_Spend.min(),xmax=data.RD_Spend.max(),
color='red',linestyles='--')
#添加轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')
#设置第二张子图的位置
ax2=plt.subplot2grid(shape=(2,1),loc=(1,0))
ax2.scatter(data.Marketing_Spend,(model.resid-model.resid.mean())/model.resid.std())
ax2.hlines(y=0,xmin=data.Marketing_Spend.min(),xmax=data.Marketing_Spend.max(),
color='red',linestyles='--')
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')
#调整子图之间的水平距离和高度距离
plt.subplots_adjust(hspace=0.6,wspace=0.3)
plt.show()
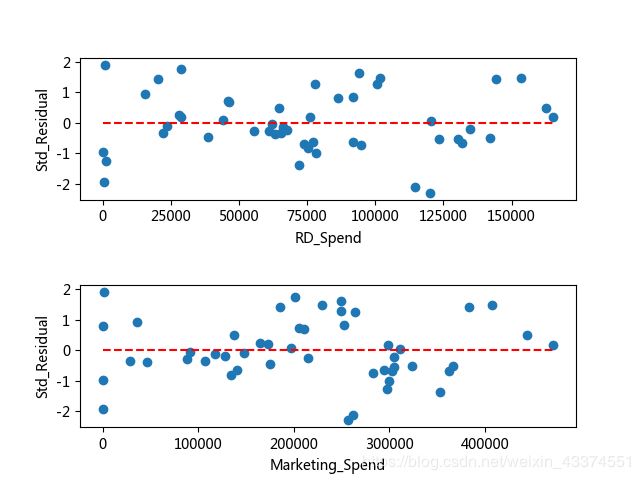
标准化残差点均匀的分布在参考线y=0的附近,说明满足方差齐性。
(2)BP检验:
拉格朗日乘子LM统计量,原假设为残差的方差是一个常数。
import pandas as pd
from statsmodels.api import formula as smf
from statsmodels.api import stats
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
model=smf.ols('Profit~RD_Spend+Marketing_Spend',data=data).fit()
print(stats.diagnostic.het_breuschpagan(model.resid,exog_het=model.model.exog))
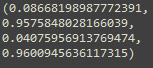
第一个值为LM统计量,第二个值为LM统计量的p值,第三个值为F统计量(检验残差的平方与自变量之间是否独立),第四个值为F统计量的p值。
如果残差不满足齐性,可以用两种方法解决:一是模型变换法,即考虑残差与自变量之间的关系,如果残差与自变量x成正比,模型两边同时除以 x \sqrt x x,如果残差与自变量x的平方成正比,模型两边同时除以x;二是加权最小二乘法,用三种权重进行对比测试(残差绝对值的倒数作为权重、残差平方的倒数作为权重、残差的平方对数与自变量x重新拟合建模得到的拟合值取指数,用指数的倒数作为权重)
7.异常值检验
(1)帽子矩阵
帽子矩阵考察的是第i个样本对观测值 y ^ \hat y y^的影响大小。
y ^ = X β ^ = X ( X T X ) − 1 X T y = H y \hat y=X\hat\beta=X(X^TX)^{-1}X^Ty=Hy y^=Xβ^=X(XTX)−1XTy=Hy其中 H = X ( X T X ) − 1 X T H=X(X^TX)^{-1}X^T H=X(XTX)−1XT就是帽子矩阵,样本为异常值的判断方法:
h i i ≥ 2 ( p + 1 ) n h_{ii}\geq\frac{2(p+1)}{n} hii≥n2(p+1)其中 h i i h_{ii} hii为帽子矩阵H的第i个主对角线元素,p为自变量个数,n为样本量。
(2)DFFITS准则
同样是根据帽子矩阵构造了一个统计量:
D i ( σ ) = h i i 1 − h i i ε i σ 1 − h i i D_i(\sigma)=\sqrt{\frac{h_{ii}}{1-h_{ii}}}\frac{\varepsilon_i}{\sigma\sqrt{1-h_{ii}}} Di(σ)=1−hiihiiσ1−hiiεi其中 h i i h_{ii} hii为帽子矩阵H的第i个主对角线元素, ε i \varepsilon_i εi为第i个样本点的预测误差, σ \sigma σ为误差项的标准差,样本为异常值的判断方法:
∣ D i ( σ ) ∣ > 2 p + 1 n |D_i(\sigma)|>2\sqrt{\frac{p+1}{n}} ∣Di(σ)∣>2np+1
(3)学生化残差
判断方法:
r i = ε i σ 1 − h i i > 2 r_i=\frac{\varepsilon_i}{\sigma\sqrt{1-h_{ii}}}>2 ri=σ1−hiiεi>2
(4)Cook距离
Cook距离没有具体的临界值判断样本是否为异常点,Cook统计量越大,是异常点的可能性越大。
D i s t a n c e i = 1 p + 1 ( h i i 1 − h i i ) r i 2 Distance_i=\frac{1}{p+1}\left (\frac{h_{ii}}{1-h_{ii}}\right)r_i^2 Distancei=p+11(1−hiihii)ri2其中 r i r_i ri为学生化残差。
import pandas as pd
import numpy as np
from statsmodels.api import formula as smf
data=pd.read_excel(r'C:\Users\sc\Desktop\Predict to Profit.xlsx')
model=smf.ols('Profit~RD_Spend+Marketing_Spend',data=data).fit()
#异常值检验
outliers=model.get_influence()
#帽子矩阵
leverage=outliers.hat_matrix_diag
#DFFITS值
dffits=outliers.dffits[0]
#学生化残差
resid_stu=outliers.resid_studentized_external
#cook距离
cook=outliers.cooks_distance[0]
#合并各种异常值检验的统计量值
contat1=pd.concat([pd.Series(leverage,name='leverage'),pd.Series(dffits,name='dffits'),
pd.Series(resid_stu,name='resid_stu'),pd.Series(cook,name='cook')],axis=1)
##重设train数据的行索引
#train.index=range(train.shape[0])
#合并数据和异常值
profit_outliers=pd.concat([data,contat1],axis=1)
#计算异常值数量的比例,以学生化残差为例
outliers_ratio=sum(np.where((np.abs(profit_outliers.resid_stu)>2),1,0))/data.shape[0]
print(outliers_ratio)
如果异常值比例较小,比如小于5%,可以考虑直接删除异常值;如果比例比较高,则不能直接删除,要设置成哑变量,即对于异常点哑变量值为1,否则为0。
参考文献:
[1]Peter Harrington.《机器学习实战》.人民邮电出版社,2013-6
[2]刘顺祥.《从零开始学Python数据分析与挖掘》.清华大学出版社,2018