中国象棋python实现(拥有完整源代码) Alpha-beta剪枝+GUI+历史启发式+有普通人棋力
目录
- 摘要
- 源代码下载
- 效果
- 走法计算
- 评估函数与搜索
- Alpha-beta搜索算法介绍
- 评价函数详解
- 历史启发式算法
- UI设计
- 算法介绍
摘要
不用神经网络强化学习,只用搜索实现的下象棋!我们的中国象棋使用python实现,总共2000+行代码,分为走法计算、评估函数与搜索和UI三部分,并采用历史启发算法进行优化,有着不错的效果。可以实现正常的人机对战,有着普通人的棋力。
源代码下载
为了方便大家下载,这里提供了两种不同下载方式。
github完整源代码下载
百度云完整源代码下载。
链接:https://pan.baidu.com/s/1OEoUUVGbI81LsaQTdSmy2Q
提取码:nmd0
效果
搜索深度:
我们的算法在搜索深度为4的时候可以达到立刻出结果的效果,经过优化后平均搜索步数为10000左右,在搜索深度为6的时候平均搜索步数为90万左右,计算较为缓慢。深度不能太深的原因是,这个搜索算法本身就是指数级别复杂度,就算进行优化,也只能减小常数,而且评估函数复杂,所以使用这种方法深度不能太深,不然只能牺牲精度。
棋力效果:
我们设计的评估函数较为详细,考虑方面周全,基本具备一个正常人的棋力。
具体效果如下(6步时):
走法计算
def generate_move(self, who): # 返回所有可行的走法, 一个step类型的list
res_list = []
for x in range(9):
for y in range(10):
if self.board[x][y].chess_type != 0:
if self.board[x][y].belong != who:
continue
list2 = self.get_chess_move(x, y, who) # 返回每个棋子的走法
# print(list2)
res_list = res_list + list2
return res_list
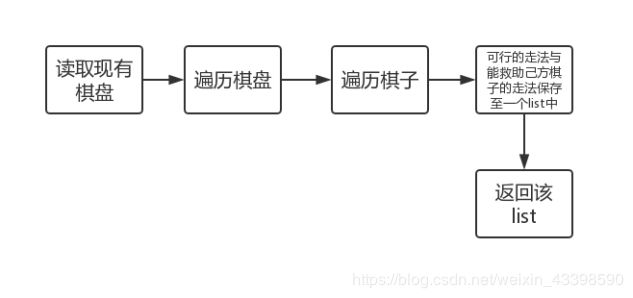
评估函数与搜索
流程图如下:
Alpha-beta搜索算法介绍
Alpha-beta搜索使用一颗n叉树来表示整个下棋的流程。电脑在选择走棋的时候,会尽可能选择对自己最有利的走法。可以通过尝试每一种走法,然后对每种局面进行比较,最终选出能够对自己最有利的走法。
在使用alpha-beta搜索算法需要遍历整个n叉树,我们可以看出搜索每迭代一层,复杂度就指数级增长。通常中国象棋合理的招数多达50种,所以每增加一层复杂度增加50倍。在搜索六步时的复杂度接近200亿,在搜索10步的时候复杂度超过几千万亿。所以搜索复杂度很高,效率较低。
象棋是博弈的过程,我们需要让自己的局面最优,让对手的局面最劣。Alpha-beta的算法就是在搜索的过程中利用已知信息进行剪枝的实现方法。它的实现基于一种想法:如果已经有选择比当下选择更好,那么只要能证明当下选择劣于某个更好选择,就可以进行剪枝,不需要对这种选择继续进行考虑。
Alpha-beta算法在搜索时,始终记录节点的α值和β值。其中α值是该节点的子节点能到达的最大值,β值是该节点的子节点能够到达的最小值。通过比较不同节点之间的α、β值来进行剪枝。例如某个子节点的得分<=α时,可以直接剪枝;某个子节点得分>=β时,也可以进行剪枝,因为对手可以通过之前的某种策略避免这种情况的发生。
算法核心实现如下
def alpha_beta(self, depth, alpha, beta): # alpha-beta剪枝,alpha是大可能下界,beta是最小可能上界
who = (self.max_depth - depth) % 2 # 那个玩家
if self.is_game_over(who): # 判断是否游戏结束,如果结束了就不用搜了
return cc.min_val
if depth == 1: # 搜到指定深度了,也不用搜了
# print(self.evaluate(who))
return self.evaluate(who)
move_list = self.board.generate_move(who) # 返回所有能走的方法
# 利用历史表0
for i in range(len(move_list)):
move_list[i].score = self.history_table.get_history_score(who, move_list[i])
move_list.sort() # 为了让更容易剪枝利用历史表得分进行排序
best_step = move_list[0]
score_list = []
for step in move_list:
temp = self.move_to(step)
score = -self.alpha_beta(depth - 1, -beta, -alpha) # 因为是一层选最大一层选最小,所以利用取负号来实现
score_list.append(score)
self.undo_move(step, temp)
if score > alpha:
alpha = score
if depth == self.max_depth:
self.best_move = step
best_step = step
if alpha >= beta:
best_step = step
break
# print(score_list)
# 更新历史表
if best_step.from_x != -1:
self.history_table.add_history_score(who, best_step, depth)
return alpha
评价函数详解
如一种所说,在搜索过程中需要记录节点的α值和β值。所以需要在每个叶子节点对当前局面进行评价来表示局面的优劣。评价函数的合理性将直接影响整个程序的性能。好的评价函数能够考虑到场面上的各种配合等等,从而对局面做出最正确的判断,所以在实现评价函数的时候需要考虑种种因素:
- 棋子的固定子力值。每种类型的棋子都有各自本身的子力价值。一般而言,子力值越大越重要,哪一方的固定子力值和大,则该方占优;否则处于劣势。具体每个棋子的子力值多少,不同设计者的经验不同,给出的具体值不同,所产生的效果也不同。
| 将 | 士 | 象 | 马 | 车 | 炮 | 卒 |
|---|---|---|---|---|---|---|
| 10000 | 250 | 250 | 300 | 500 | 300 | 80 |
-
棋子的位置价值。中国象棋局势不仅仅取决于子力大小,更与棋子位置联系巨大。棋子在不同位置上应该给予不同的评价。例如卒在初始位置时,作用较小,位置值较小;而当卒进入对方九宫格之后对对方威胁极大,位置值较大。再例如,当头炮的威胁值较大,而在其他路的时候威胁则稍微小一些。因此也需要根据设计者的经验,对不同棋子不同位置的价值给予不同的评价。
-
棋子灵活度评估值。棋子威力的发挥取决于其灵活度。灵活度高的棋子,例如车,可以在战场上快速发挥作用,评价值较高。而灵活度较差的棋子则评分较低。
| 将 | 车 | 马 | 炮 | 相 | 士 | 兵 |
|---|---|---|---|---|---|---|
| 0 | 6 | 12 | 6 | 1 | 1 | 15 |
-
棋子威胁、保护评估值。每个棋子可能处于对方威胁下,也可能处于己放棋子保护之中。这将直接影响到这颗棋子的安全系数,进而影响战局。因此需要考虑被威胁和保护的棋子。当棋子处于威胁之中时,应当降低评价值;当棋子处于保护之中时,应当增加评价值。
我们分了不同数量保护的情况,来进行局面关系评分,核心代码如下:
for x in range(9): for y in range(10): num_attacked = relation_list[x][y].num_attacked num_guarded = relation_list[x][y].num_guarded now_chess = self.board.board[x][y] type = now_chess.chess_type now = now_chess.belong unit_val = cc.base_val[now_chess.chess_type] >> 3 sum_attack = 0 # 被攻击总子力 sum_guard = 0 min_attack = 999 # 最小的攻击者 max_attack = 0 # 最大的攻击者 max_guard = 0 flag = 999 # 有没有比这个子的子力小的 if type == cc.kong: continue # 统计攻击方的子力 for i in range(num_attacked): temp = cc.base_val[relation_list[x][y].attacked[i]] flag = min(flag, min(temp, cc.base_val[type])) min_attack = min(min_attack, temp) max_attack = max(max_attack, temp) sum_attack += temp # 统计防守方的子力 for i in range(num_guarded): temp = cc.base_val[relation_list[x][y].guarded[i]] max_guard = max(max_guard, temp) sum_guard += temp if num_attacked == 0: relation_val[now] += 5 * relation_list[x][y].num_guarded else: muti_val = 5 if who != now else 1 if num_guarded == 0: # 如果没有保护 relation_val[now] -= muti_val * unit_val else: # 如果有保护 if flag != 999: # 存在攻击者子力小于被攻击者子力,对方将愿意换子 relation_val[now] -= muti_val * unit_val relation_val[1 - now] -= muti_val * (flag >> 3) # 如果是二换一, 并且最小子力小于被攻击者子力与保护者子力之和, 则对方可能以一子换两子 elif num_guarded == 1 and num_attacked > 1 and min_attack < cc.base_val[type] + sum_guard: relation_val[now] -= muti_val * unit_val relation_val[now] -= muti_val * (sum_guard >> 3) relation_val[1 - now] -= muti_val * (flag >> 3) # 如果是三换二并且攻击者子力较小的二者之和小于被攻击者子力与保护者子力之和,则对方可能以两子换三子 elif num_guarded == 2 and num_attacked == 3 and sum_attack - max_attack < cc.base_val[type] + sum_guard: relation_val[now] -= muti_val * unit_val relation_val[now] -= muti_val * (sum_guard >> 3) relation_val[1 - now] -= muti_val * ((sum_attack - max_attack) >> 3) # 如果是n换n,攻击方与保护方数量相同并且攻击者子力小于被攻击者子力与保护者子力之和再减去保护者中最大子力,则对方可能以n子换n子 elif num_guarded == num_attacked and sum_attack < cc.base_val[now_chess.chess_type] + sum_guard - max_guard: relation_val[now] -= muti_val * unit_val relation_val[now] -= muti_val * ((sum_guard - max_guard) >> 3) relation_val[1 - now] -= sum_attack >> 3 -
将帅安全评估值。将帅的安全整局游戏的关键。需要从将的位置以及和其他棋子的位置关系中体现出来;例如当头炮、窝心马对将帅的威胁较大,体现在这些棋子的位置价值中。
pos_val = [ [ # 空 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [ # 将 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, -8, -9, 0, 0, 0, 0, 0, 0, 0, 5, -8, -9, 0, 0, 0, 0, 0, 0, 0, 1, -8, -9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ], [ # 车 -6, 5, -2, 4, 8, 8, 6, 6, 6, 6, 6, 8, 8, 9, 12, 11, 13, 8, 12, 8, 4, 6, 4, 4, 12, 11, 13, 7, 9, 7, 12, 12, 12, 12, 14, 14, 16, 14, 16, 13, 0, 0, 12, 14, 15, 15, 16, 16, 33, 14, 12, 12, 12, 12, 14, 14, 16, 14, 16, 13, 4, 6, 4, 4, 12, 11, 13, 7, 9, 7, 6, 8, 8, 9, 12, 11, 13, 8, 12, 8, -6, 5, -2, 4, 8, 8, 6, 6, 6, 6 ], [ # 马 0, -3, 5, 4, 2, 2, 5, 4, 2, 2, -3, 2, 4, 6, 10, 12, 20, 10, 8, 2, 2, 4, 6, 10, 13, 11, 12, 11, 15, 2, 0, 5, 7, 7, 14, 15, 19, 15, 9, 8, 2, -10, 4, 10, 15, 16, 12, 11, 6, 2, 0, 5, 7, 7, 14, 15, 19, 15, 9, 8, 2, 4, 6, 10, 13, 11, 12, 11, 15, 2, -3, 2, 4, 6, 10, 12, 20, 10, 8, 2, 0, -3, 5, 4, 2, 2, 5, 4, 2, 2 ], [ # 炮 0, 0, 1, 0, -1, 0, 0, 1, 2, 4, 0, 1, 0, 0, 0, 0, 3, 1, 2, 4, 1, 2, 4, 0, 3, 0, 3, 0, 0, 0, 3, 2, 3, 0, 0, 0, 2, -5, -4, -5, 3, 2, 5, 0, 4, 4, 4, -4, -7, -6, 3, 2, 3, 0, 0, 0, 2, -5, -4, -5, 1, 2, 4, 0, 3, 0, 3, 0, 0, 0, 0, 1, 0, 0, 0, 0, 3, 1, 2, 4, 0, 0, 1, 0, -1, 0, 0, 1, 2, 4 ], [ # 相 0, 0, -2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -2, 0, 0, 0, 0, 0, 0, 0 ], [ # 士 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ], [ # 兵 0, 0, 0, -2, 3, 10, 20, 20, 20, 0, 0, 0, 0, 0, 0, 18, 27, 30, 30, 0, 0, 0, 0, -2, 4, 22, 30, 45, 50, 0, 0, 0, 0, 0, 0, 35, 40, 55, 65, 2, 0, 0, 0, 6, 7, 40, 42, 55, 70, 4, 0, 0, 0, 0, 0, 35, 40, 55, 65, 2, 0, 0, 0, -2, 4, 22, 30, 45, 50, 0, 0, 0, 0, 0, 0, 18, 27, 30, 30, 0, 0, 0, 0, -2, 3, 10, 20, 20, 20, 0 ] ]
历史启发式算法
既然Alpha-Beta搜索算法是在“最小-最大”的基础上引入“树的裁剪”的思想以期提高效率,那么它的效率将在很大程度上取决于树的结构——如果搜索了没多久就发现可以进行“裁剪”了,那么需要分析的工作量将大大减少,效率自然也就大大提高;而如果直至分析了所有的可能性之后才能做出“裁剪”操作,那此时“裁剪”也已经失去了它原有的价值(因为你已经分析了所有情况,这时的Alpha-Beta搜索已和“最小-最大”搜索别无二致了)。因而,要想保证Alpha-Beta搜索算法的效率就需要调整树的结构,即调整待搜索的结点的顺序,使得“裁剪”可以尽可能早地发生。
我们可以根据部分已经搜索过的结果来调整将要搜索的结点的顺序。因为,通常当一个局面经过搜索被认为较好时,其子结点中往往有一些与它相似的局面(如个别无关紧要的棋子位置有所不同)也是较好的。由J.Schaeffer所提出的“历史启发”(History Heuristic)就是建立在这样一种观点之上的。在搜索的过程中,每当发现一个好的走法,我们就给该走法累加一个增量以记录其“历史得分”,一个多次被搜索并认为是好的走法的“历史得分”就会较高。对于即将搜索的结点,按照“历史得分”的高低对它们进行排序,保证较好的走法(“历史得分”高的走法)排在前面,这样Alpha-Beta搜索就可以尽可能早地进行“裁剪”,从而保证了搜索的效率。
class history_table: # 历史启发算法
def __init__(self):
self.table = np.zeros((2, 90, 90))
def get_history_score(self, who, step):
return self.table[who, step.from_x * 9 + step.from_y, step.to_x * 9 + step.to_y]
def add_history_score(self, who, step, depth):
self.table[who, step.from_x * 9 + step.from_y, step.to_x * 9 + step.to_y] += 2 << depth
经过我们的测试,加入历史启发式算法后,计算的速度提高了6-7倍。
UI设计
算法介绍
UI设计之需要将棋盘填好,并使得人机对战时,人的走法可以通过鼠标移动位置决定即可,电脑走法 与ai算法有关
流程图如下:
核心代码如下:
def PutdownPieces(self, t, x, y):
selectfilter=list(filter(lambda cm: cm.x == x and cm.y == y and cm.player == MainGame.player1Color,MainGame.piecesList))
if len(selectfilter):
MainGame.piecesSelected = selectfilter[0]
return
if MainGame.piecesSelected :
#print("1111")
arr = pieces.listPiecestoArr(MainGame.piecesList)
if MainGame.piecesSelected.canmove(arr, x, y):
self.PiecesMove(MainGame.piecesSelected, x, y)
MainGame.Putdownflag = MainGame.player2Color
else:
fi = filter(lambda p: p.x == x and p.y == y, MainGame.piecesList)
listfi = list(fi)
if len(listfi) != 0:
MainGame.piecesSelected = listfi[0]
def PiecesMove(self,pieces, x , y):
for item in MainGame.piecesList:
if item.x ==x and item.y == y:
MainGame.piecesList.remove(item)
pieces.x = x
pieces.y = y
print("move to " +str(x) +" "+str(y))
return True
def Computerplay(self):
if MainGame.Putdownflag == MainGame.player2Color:
print("轮到电脑了")
computermove = computer.getPlayInfo(MainGame.piecesList, self.from_x, self.from_y, self.to_x, self.to_y, self.mgInit)
if computer==None:
return
piecemove = None
for item in MainGame.piecesList:
if item.x == computermove[0] and item.y == computermove[1]:
piecemove= item
self.PiecesMove(piecemove, computermove[2], computermove[3])
MainGame.Putdownflag = MainGame.player1Color
#判断游戏胜利
def VictoryOrDefeat(self):
txt =""
result = [MainGame.player1Color,MainGame.player2Color]
for item in MainGame.piecesList:
if type(item) ==pieces.King:
if item.player == MainGame.player1Color:
result.remove(MainGame.player1Color)
if item.player == MainGame.player2Color:
result.remove(MainGame.player2Color)
if len(result)==0:
return
if result[0] == MainGame.player1Color :
txt = "失败!"
else:
txt = "胜利!"
MainGame.window.blit(self.getTextSuface("%s" % txt), (constants.SCREEN_WIDTH - 100, 200))
MainGame.Putdownflag = constants.overColor
可以实现UI与算法的对接,使得坐标与棋子对应,棋子可以正确的根据算法结果或者鼠标坐标来移动