python数据分析与挖掘实战 之笔记1
《python数据分析与挖掘实战》学习笔记
一、一二三章笔记(简写)
1、利用scipy包求解非线性方程组的解
2 x 1 − x 2 = 1 2x_{1}-x^{2}=1 2x1−x2=1 x 1 2 − x 2 = 2 x_1^2-x_2=2 x12−x2=2
from scipy.optimize import fsolve #导入求解方程组的函数
def f(x): #定义要求解的方程组
x1 = x[0]
x2 = x[1]
return [2*x1 - x2**2 - 1, x1**2 - x2 -2]
result = fsolve(f, [1,1]) #输入初值[1, 1]并求解
print(result) #输出结果,为array([ 1.91963957, 1.68501606])
2、进行积分运算
∫ − 1 1 1 − x 2 d x \int_{-1}^{1}\sqrt{1-x^{2}}dx ∫−111−x2dx
from scipy import integrate #导入积分函数
def g(x): #定义被积函数
return (1-x**2)**0.5
pi_2, err = integrate.quad(g, -1, 1) #积分结果和误差
print(pi_2 * 2) #由微积分知识知道积分结果为圆周率pi的一半
print(pi_2,err)
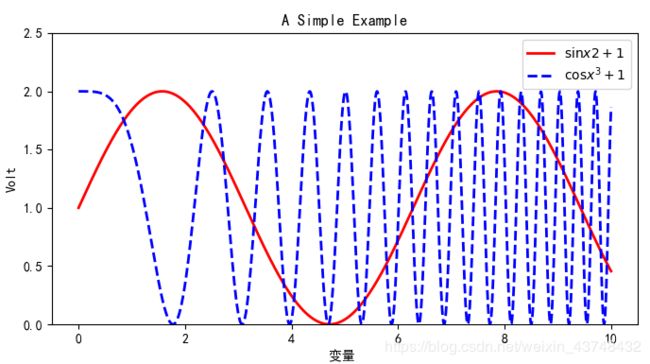
import numpy as np
import matplotlib.pyplot as plt #导入Matplotlib
plt.rcParams['font.sans-serif'] = ['SimHei']
x = np.linspace(0, 10, 1000) #作图的变量自变量
y = np.sin(x) + 1 #因变量y
z = np.cos(x**2) + 1 #因变量z
plt.figure(figsize = (8, 4)) #设置图像大小
plt.plot(x,y,label = '$\sin x2+1$', color = 'red', linewidth = 2) #作图,设置标签、线条颜色、线条大小
plt.plot(x, z, 'b--', label = '$\cos x^3+1$',color = 'blue', linewidth = 2) #作图,设置标签、线条类型
plt.xlabel('变量 ') # x轴名称
plt.ylabel('Volt') # y轴名称
plt.title('A Simple Example') #标题
plt.ylim(0, 2.5) #显示的y轴范围
plt.legend() #显示图例
plt.show() #显示作图结果
4、绘制箱线图
import pandas as pd
catering_sale = '../data/catering_sale.xls' #餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据,指定“日期”列为索引列
#data = data[(data[u'销量'] > 400)&(data[u'销量'] < 5000)] #过滤异常数据
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure() #建立图像
p = data.boxplot(return_type='dict') #画箱线图,直接使用DataFrame的方法
x = p['fliers'][0].get_xdata() # 'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort() #从小到大排序,该方法直接改变原对象
#用annotate添加注释
#其中有些相近的点,注解会出现重叠,难以看清,需要一些技巧来控制。
#以下参数都是经过调试的,需要具体问题具体调试。
for i in range(len(x)):
if i>0:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
else:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))
plt.title('箱线图')
plt.show() #展示箱线图
from __future__ import print_function
import pandas as pd
#初始化参数
dish_profit = '../data/catering_dish_profit.xls' #餐饮菜品盈利数据
data = pd.read_excel(dish_profit, index_col='菜品名')
data = data['盈利'].copy()
data.sort_values(ascending = False)
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure()
data.plot(kind='bar')
plt.ylabel('盈利(元)')
p = 1.0*data.cumsum()/data.sum()
p.plot(color = 'r', secondary_y=True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy=(6, p[6]), xytext=(6*0.9, p[6]*0.9),
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
#添加注释,即85%处的标记。这里包括了指定箭头样式。
plt.ylabel('盈利(比例)')
plt.show()
二、第四章 数据预处理
1、数据清洗
其主要是删除原始数据中无关数据、重复数据、平滑噪声数据,缺失值、异常值等。
处理缺失值的方法主要有:删除、插补法。
(1)拉格朗日插值法
拉格朗日多项式为:
L ( x ) = ∑ i = 0 n y i ∏ j = 0 , j ≠ i n x − x j x i − x j L(x)=\sum_{i=0}^{n}y_{i}\prod_{j=0,j\neq i}^{n}\frac{x-x_{j}}{x_{i}-x_{j}} L(x)=i=0∑nyij=0,j=i∏nxi−xjx−xj
表示为已知n个点,随机分布在空间中,无亮点在一条直线上。其分内外两层,将所缺失的x值代入多项式中,求得L缺失值。
代码如下:
在这里插入代码片
(2)牛顿插值法
f ( x ) = f ( x 1 ) + ( x − x 1 ) f [ x 2 , x 1 ] + ( x − x 1 ) ( x − x 2 ) f [ x 3 , x 2 , x 1 ] + ⋯ + ( x − x 1 ) ( x − x 2 ) ⋯ ( x − x n − 1 ) f [ x n , ⋯ x 2 , x 1 ] + ( x − x 1 ) ( x − x 2 ) ⋯ ( x − x n ) f [ x n , ⋯ x 2 , x 1 , x ] = P ( x ) + R ( x ) f(x)=f(x_1)+(x-x_1)f[x_2,x_1]+(x-x_1)(x-x_2)f[x_3,x_2,x_1]+\cdots +\\ (x-x_1)(x-x_2)\cdots (x-x_{n-1})f[x_n,\cdots x_2,x_1]\\ +(x-x_1)(x-x_2)\cdots (x-x_{n})f[x_n,\cdots x_2,x_1,x]\\ =P(x)+R(x) f(x)=f(x1)+(x−x1)f[x2,x1]+(x−x1)(x−x2)f[x3,x2,x1]+⋯+(x−x1)(x−x2)⋯(x−xn−1)f[xn,⋯x2,x1]+(x−x1)(x−x2)⋯(x−xn)f[xn,⋯x2,x1,x]=P(x)+R(x)
其中:p(x)为牛顿插值逼近函数,R(x)是误差函数。
P ( x ) = f ( x 1 ) + ( x − x 1 ) f [ x 2 , x 1 ] + ( x − x 1 ) ( x − x 2 ) f [ x 3 , x 2 , x 1 ] + ⋯ + ( x − x 1 ) ( x − x 2 ) ⋯ ( x − x n − 1 ) f [ x n , ⋯ x 2 , x 1 ] P(x)=f(x_1)+(x-x_1)f[x_2,x_1]+(x-x_1)(x-x_2)f[x_3,x_2,x_1]+\\ \cdots +(x-x_1)(x-x_2)\cdots (x-x_{n-1})f[x_n,\cdots x_2,x_1] P(x)=f(x1)+(x−x1)f[x2,x1]+(x−x1)(x−x2)f[x3,x2,x1]+⋯+(x−x1)(x−x2)⋯(x−xn−1)f[xn,⋯x2,x1]
R ( x ) = ( x − x 1 ) ( x − x 2 ) ⋯ ( x − x n ) f [ x n , ⋯ x 2 , x 1 , x ] R(x)=(x-x_1)(x-x_2)\cdots (x-x_{n})f[x_n,\cdots x_2,x_1,x] R(x)=(x−x1)(x−x2)⋯(x−xn)f[xn,⋯x2,x1,x]
代码如下所示:
(3)异常值处理
对于异常值可以进行删除,但数据量较小时,不建议使用;也可以按照其他已知条件按缺失值处理。(后续所学得再做笔记)
2、数据集成
考虑实体识别问题和属性冗余问题
3、数据变换
(1)简单函数变换
求平方、开方、取对数、差分等,使不具有正态分布的数据变换成具有正态分布的数据。
(2)规范化
①离差标准化
②标准差标准化
x ∗ = x − x ˉ σ x^{*}=\frac{x-\bar{x}}{\sigma} x∗=σx−xˉ
③小数位标准化
处理如下数据:

代码如下所示:
import pandas as pd
import numpy as np
datafile = '../data/normalization_data.xls' #参数初始化
data = pd.read_excel(datafile, header = None) #读取数据
print((data - data.min())/(data.max() - data.min()))#最小-最大规范化
print((data - data.mean())/data.std()) #零-均值规范化
print(data/10**np.ceil(np.log10(data.abs().max()))) #小数定标规范化
结果如下所示:
0 1 2 3
0 0.074380 0.937291 0.923520 1.000000
1 0.619835 0.000000 0.000000 0.850941
2 0.214876 0.119565 0.813322 0.000000
3 0.000000 1.000000 1.000000 0.563676
4 1.000000 0.942308 0.996711 0.804149
5 0.264463 0.838629 0.814967 0.909310
6 0.636364 0.846990 0.786184 0.929571
0 1 2 3
0 -0.905383 0.635863 0.464531 0.798149
1 0.604678 -1.587675 -2.193167 0.369390
2 -0.516428 -1.304030 0.147406 -2.078279
3 -1.111301 0.784628 0.684625 -0.456906
4 1.657146 0.647765 0.675159 0.234796
5 -0.379150 0.401807 0.152139 0.537286
6 0.650438 0.421642 0.069308 0.595564
0 1 2 3
0 0.078 0.521 0.602 0.2863
1 0.144 -0.600 -0.521 0.2245
2 0.095 -0.457 0.468 -0.1283
3 0.069 0.596 0.695 0.1054
4 0.190 0.527 0.691 0.2051
5 0.101 0.403 0.470 0.2487
6 0.146 0.413 0.435 0.2571
(3)连续属性离散化
由于某些分类算法,需要分类属性的数据,我们需要将连续属性离散化。
方法有:等宽法(类似频率分布表)、等频法、k-均值聚类法。
处理如下数据(部分):
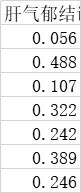
代码如下:
import pandas as pd
datafile = '../data/discretization_data.xls' #参数初始化
data = pd.read_excel(datafile) #读取数据
data = data[u'肝气郁结证型系数'].copy()
k = 4
d1 = pd.cut(data, k, labels = range(k)) #等宽离散化,各个类比依次命名为0,1,2,3
#等频率离散化
w = [1.0*i/k for i in range(k+1)]
w = data.describe(percentiles = w)[4:4+k+1] #使用describe函数自动计算分位数
w[0] = w[0]*(1-1e-10)
d2 = pd.cut(data, w, labels = range(k))
from sklearn.cluster import KMeans #引入KMeans
kmodel = KMeans(n_clusters = k, n_jobs = 4) #建立模型,n_jobs是并行数,一般等于CPU数较好
kmodel.fit(data.values.reshape((len(data), 1))) #训练模型
c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0) #输出聚类中心,并且排序(默认是随机序的)
w = c.rolling(2).mean().iloc[1:] #相邻两项求中点,作为边界点
w = [0] + list(w[0]) + [data.max()] #把首末边界点加上
d3 = pd.cut(data, w, labels=range(k))
def cluster_plot(d, k): #自定义作图函数来显示聚类结果
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure(figsize = (8, 3))
for j in range(0, k):
plt.plot(data[d==j], [j for i in d[d==j]], 'o')
plt.ylim(-0.5, k-0.5)
return plt
cluster_plot(d1, k).show()
cluster_plot(d2, k).show()
cluster_plot(d3, k).show()
结果如下:



(4)小波变换
所谓小波变换是指:(这里只写了大致的内容,后面会继续深入学习)
①对小波基函数进行伸缩和平移变换:
ψ a , b ( t ) = 1 ∣ a ∣ ψ ( t − b a ) \psi _{a,b}(t)=\frac{1}{\sqrt{\left | a \right |}}\psi (\frac{t-b}{a}) ψa,b(t)=∣a∣1ψ(at−b)
ψ \psi ψ()为小波基函数,a为伸缩因子,b为平移因子。
②任意函数 f ( t ) f(t) f(t)的连续小波变换(CWT)可以表示为:
W f ( a , b ) = 1 ∣ a ∣ ∫ f ( t ) ψ ( t − b a ) d t W_{f}(a,b)=\frac{1}{\sqrt{\left | a \right |}}\int f(t)\psi (\frac{t-b}{a})dt Wf(a,b)=∣a∣1∫f(t)ψ(at−b)dt
③连续小波变换为 f ( t ) f(t) f(t)—— W f ( a , b ) W_{f}(a,b) Wf(a,b)的映射,对小波基函数增加约束条件:
C ψ = ∫ ∣ ψ ( t ) ~ ∣ 2 t d t < ∞ C_{\psi }=\int \frac{\left | \tilde{\psi(t)} \right |^{2}}{t}dt<\infty Cψ=∫t∣∣∣ψ(t)~∣∣∣2dt<∞
则可由 W f ( a , b ) W_{f}(a,b) Wf(a,b)逆变换得到 f ( t ) f(t) f(t)。其中小波函数进行了傅里叶变换。
④得到逆变换结果为:
f ( t ) = 1 C ψ ∫ ∫ 1 a 2 W f ( a , b ) ψ ( t − b a ) d a d b f(t)=\frac{1}{C_{\psi }}\int \int \frac{1}{a^{2}}W_{f}(a,b)\psi (\frac{t-b}{a})dadb f(t)=Cψ1∫∫a21Wf(a,b)ψ(at−b)dadb
下面利用小波变换的多尺度空间能量分布对声波信号进行特征提取,即从声波信号到特征向量数据的变换。
首先分解小波,其次计算总能量,最后构造特征向量。代码如下所示:
#参数初始化
inputfile= '../data/leleccum.mat' #提取自Matlab的信号文件
from scipy.io import loadmat #mat是MATLAB专用格式,需要用loadmat读取它
mat = loadmat(inputfile)
signal = mat['leleccum'][0]
import pywt #导入PyWavelets
coeffs = pywt.wavedec(signal, 'bior3.7', level = 5)
print(coeffs)
#返回结果为level+1个数字,第一个数组为逼近系数数组,后面的依次是细节系数数组
部分结果如下:
[array([2415.1478541 , 2395.74470824, 2402.22022728, 2408.90987352,
2402.22022728, 2395.74470824, 2415.1478541 , 2369.53622493,
1958.0913368 , 1983.87619596, 1901.68851538, 1651.86483216,
1482.45129628, 1356.98779058, 1257.4459793 , 1265.75505172,
4、数据规约
意义:降低无效、错误数据对建模的影响,提高建模的准确性;少量且具有代表性的数据进行挖掘会降低挖掘时间; 降低储存成本。
(1)属性规约
其目标是寻找出最小的属性子集并确保新数据子集的概率分布尽可能的接近原来的数据集的概率分布。
主成分分析:
原理:利用降维的思想将多数指标转为低维指标。步骤如下:
①原始数据,变量指标共p个,其n次观测数据矩阵如下:
X = [ x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋯ ⋯ ⋯ ⋯ x n 1 x n 2 ⋯ x n p ] X=\begin{bmatrix} x11& x12& \cdots & x1p&\\ x21& x22& \cdots & x2p&\\ \cdots & \cdots & \cdots &\cdots&\\ xn1& xn2& \cdots & xnp& \end{bmatrix} X=⎣⎢⎢⎡x11x21⋯xn1x12x22⋯xn2⋯⋯⋯⋯x1px2p⋯xnp⎦⎥⎥⎤
②对该矩阵进行标准化处理,仍计为 X X X。
③求其相关系数矩阵 R R R, R = ( r i j ) p × p R=(r_{ij})_{p×p} R=(rij)p×p,其具体定义如下所示:
r i j = ∑ k = 1 n ( x k i − x i ˉ ) ( x k j − x j ˉ ) ∑ k = 1 n ( x k i − x i ˉ ) 2 ∑ k = 1 n ( x k j − x j ˉ ) 2 r_{ij}=\frac{\sum_{k=1}^{n}(x_{ki}-\bar{x_i})(x_{kj}-\bar{x_j})}{\sqrt{\sum_{k=1}^{n}(x_{ki}-\bar{x_i})^{2}\sum_{k=1}^{n}(x_{kj}-\bar{x_j})^{2}}} rij=∑k=1n(xki−xiˉ)2∑k=1n(xkj−xjˉ)2∑k=1n(xki−xiˉ)(xkj−xjˉ)
其中, r i j = r j i r_{ij}=r_{ji} rij=rji, r i i = 1 r_{ii}=1 rii=1.
④求 R R R的特征根。即 d e t ( R − λ E ) = 0 det(R-\lambda E)=0 det(R−λE)=0,得到特征根为 λ 1 ⩾ λ 2 ≥ λ p > 0 \lambda_1\geqslant \lambda _2\geq \lambda _p>0 λ1⩾λ2≥λp>0。
⑤按照方差贡献率确定主成分个数。从p个中降维为m个成分。一般提取80%以上。
其贡献率按如下方式计算: ∑ i = 1 m λ i ∑ i = 1 p λ i ⩾ 80 % \frac{\sum_{i=1}^{m}\lambda _i}{\sum_{i=1}^{p}\lambda _i}\geqslant80\% ∑i=1pλi∑i=1mλi⩾80%
⑥计算所提取的m个相应的单位特征向量:
α 1 , α 2 , . . . , α m \alpha _1,\alpha _2,...,\alpha _m α1,α2,...,αm均为p×1维的数据
⑦计算主成分为:
Z i = β 1 i X 1 + β 2 i X 2 + ⋯ + β p i X p , i = 1 , 2 , ⋯ , m Z_i=\beta _{1i}X_1+\beta _{2i}X_2+\cdots +\beta _{pi}X_p,i=1,2,\cdots ,m Zi=β1iX1+β2iX2+⋯+βpiXp,i=1,2,⋯,m
原始数据为:
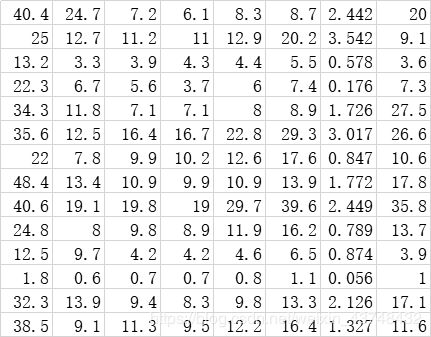
代码如下所示:
import pandas as pd
#参数初始化
inputfile = '../data/principal_component.xls'
outputfile = 'dimention_reducted.xls' #降维后的数据
data = pd.read_excel(inputfile, header = None) #读入数据
from sklearn.decomposition import PCA #导入主成分分析库
pca = PCA()
pca.fit(data)
print(pca.components_)#返回模型的各个特征向量
print(pca.explained_variance_ratio_) #返回各个成分各自的方差百分比
结果如下:
主成分:[[ 0.56788461 0.2280431 0.23281436 0.22427336 0.3358618 0.43679539
0.03861081 0.46466998]
[ 0.64801531 0.24732373 -0.17085432 -0.2089819 -0.36050922 -0.55908747
0.00186891 0.05910423]
[-0.45139763 0.23802089 -0.17685792 -0.11843804 -0.05173347 -0.20091919
-0.00124421 0.80699041]
[-0.19404741 0.9021939 -0.00730164 -0.01424541 0.03106289 0.12563004
0.11152105 -0.3448924 ]
[-0.06133747 -0.03383817 0.12652433 0.64325682 -0.3896425 -0.10681901
0.63233277 0.04720838]
[ 0.02579655 -0.06678747 0.12816343 -0.57023937 -0.52642373 0.52280144
0.31167833 0.0754221 ]
[-0.03800378 0.09520111 0.15593386 0.34300352 -0.56640021 0.18985251
-0.69902952 0.04505823]
[-0.10147399 0.03937889 0.91023327 -0.18760016 0.06193777 -0.34598258
-0.02090066 0.02137393]]
贡献率:[7.74011263e-01 1.56949443e-01 4.27594216e-02 2.40659228e-02
1.50278048e-03 4.10990447e-04 2.07718405e-04 9.24594471e-05]
从上面可以看出,8个特征向量,前三个主成分的方差贡献率已经达到了95%以上。所以提取三个主成分,计算其结果为:接上面的代码
pca = PCA(3)
pca.fit(data)
low_d = pca.transform(data)#降低维度
print(low_d)
pd.DataFrame(low_d).to_excel(outputfile) #保存结果
pca.inverse_transform(low_d)#复原数据
[[ 8.19133694 16.90402785 3.90991029]
[ 0.28527403 -6.48074989 -4.62870368]
[-23.70739074 -2.85245701 -0.4965231 ]
[-14.43202637 2.29917325 -1.50272151]
[ 5.4304568 10.00704077 9.52086923]
[ 24.15955898 -9.36428589 0.72657857]
[ -3.66134607 -7.60198615 -2.36439873]
[ 13.96761214 13.89123979 -6.44917778]
[ 40.88093588 -13.25685287 4.16539368]
[ -1.74887665 -4.23112299 -0.58980995]
[-21.94321959 -2.36645883 1.33203832]
[-36.70868069 -6.00536554 3.97183515]
[ 3.28750663 4.86380886 1.00424688]
[ 5.99885871 4.19398863 -8.59953736]]
三个主成分的系数如上所示。
5、预处理的一些函数
from scipy.interpolate import * #导入其中的插值函数
from sklearn.decomposition import PCA #引入主成分分析模块