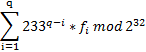2019级NOIP模拟赛
一.题解
1.队列变换
有一个调皮的班级,他们上体育课,现在排成了n行n列的一个矩形。每个人却不是面向老师,而是面向左侧或右侧。例如: RLR RRL LLR 因为老师是新来的,所以还叫不出学生的名字。他每次都是朝着一列或一行喊:向后转。这一行或这一列的L就全部变成R,R就全部变成L。因为不能让所有学生都朝一个方向,所以体育老师退而求其次,他可以允许一个人和其他人方向相反。体育老师的指令没有次数限制,他也可以对同一行或同一列进行多次发令。请找出这样的一个学生。如果最后无法使得只有一个学生和其他人方向相反,则输出“-1”。如果存在方案,则输出那一个学生的行号和列号(均从1开始)。如果有多种方案,则输出行号最小的那一个学生,如果多个学生的行坐标相等,则输出列号最小的那一个。
输入格式
第一行一个整数,表示n。 接下来是n行,每行n个字符,每一个字符为L或R。
输出格式
输出文件只有 1 行,表示那个学生的行号和列号。 如果没有,则输出-1。
样例
输入样例
3
RLR
RRL
LLR
输出样例
1 1
数据范围与提示
N<=1000
这道题是一道“模板题” , 首先说一下XZM的方法
如果我们可以把其变为全部为L,只有一个为R,那么对称过来,全为R,只有一个为L也可以
我们观察一下
c1 a1 a2 a3
c2 a4 a5 a6
c3 a7 a8 a9
r1 r2 r3
这里c[]与r[]指这一行(列)翻转了多少次
可知a1 - a2( 这里指它被翻转的次数) = r1 - r2
a4 - a5 = r1 - r2
a7 - a8 = r1- r2
也就是说,如果a1 与a2 相同 则 a4 = a5 , a7 = a8 ,反之也可
但是如果最后那个与其它点不同的点在这两行或两列,那么这个规律就一定不成立
可以用逻辑推导一下,如果a1 , a2 中有一个, a2 , a3 中有一个,那么a2 一定是答案
然后还有很多特判:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN =1003;
#define ll unsigned int
#define ull unsigned long long
int n;
int a[MAXN][MAXN];
int k[MAXN][MAXN];
int cnt0 , cnt1;
int main(){
scanf( "%d" , &n );
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= n ; j ++ ){
char c;
cin >>c;
if( c == 'L' )
a[i][j] = 0;
else
a[i][j] = 1;
}
int ans1x = 0, ans1y = 0 , ans2x = 0 , ans2y = 0;//注意任意相邻两行两列都要判断,且如果判断的答案不同,还要输出-1
bool flag = 0;
for( int i = 1 ; i < n ; i ++ ){
int sum = 0;
cnt0 = cnt1 = 0;
for( int j = 1 ; j <= n ; j ++ ){
if( !(a[i][j] ^ a[i+1][j] ) )
cnt0 ++;
else
cnt1 ++;//统计相同还是不同个数
}
if( ( cnt0 == 0 && cnt1 == n ) || ( cnt1 == 0 && cnt0 == n ) ) continue;//如果它们是满足规律,则就不管
if( cnt0 >= 2 && cnt1 >= 2 ){
printf( "-1\n" );
exit( 0 );
}//如果有大于等于两组不同,那么说明至少有两个,但是我们只有对于行的操作才有用,但是如果有两个点,就一定达不到规范
for( int j = 1 ; j <= n ; j ++ ){
if( (a[i][j] ^ a[i+1][j] ) == 0 && cnt0 == 1 ){
if( ans1x && ans1y && ans1x != i && ans1y != j && ans1x != i + 1 && ans1y != j ){
printf( "-1\n" );
exit(0);
}//如果以有找到答案,但是还有其它的点有嫌疑,输出-1
else{
flag = 1;
if( k[i][j] && k[i+1][j] ){//这也是,有两个点都是不同的,达不到目标图案
printf( "-1\n" );
exit( 0 );
}
if( k[i][j] )
ans1x = i , ans1y = j;
else if( k[i+1][j] )
ans1x = i + 1 , ans1y = j;
k[i][j] ++ , k[i+1][j] ++;
}
break;
}
else if( (a[i][j] ^ a[i+1][j] ) == 1 && cnt1 == 1 ){
if( ans1x && ans1y ){
printf( "-1\n" );
exit(0);
}
else{
flag = 1;
if( k[i][j] && k[i+1][j] ){
printf( "-1\n" );
exit( 0 );
}
if( k[i][j] )
ans1x = i , ans1y = j;
else if( k[i+1][j] )
ans1x = i + 1 , ans1y = j;
k[i][j] ++ , k[i+1][j] ++;
}
break;
}
}
}
//memset( k , 0 , sizeof( k ) );
for( int i = 1 ; i < n ; i ++ ){
int sum = 0;
cnt0 = cnt1 = 0;
for( int j = 1 ; j <= n ; j ++ ){
if( !(a[j][i] ^ a[j][i+1] ) )
cnt0 ++;
else
cnt1 ++;//统计相同还是不同个数
}
if( ( cnt0 == 0 && cnt1 == n ) || ( cnt1 == 0 && cnt0 == n ) ) continue;//如果它们是满足规律,则就不管
if( cnt0 >= 2 && cnt1 >= 2 ){
printf( "-1\n" );
exit( 0 );
}
for( int j = 1 ; j <= n ; j ++ ){
if( (a[j][i] ^ a[j][i+1] ) == 0 && cnt0 == 1 ){
if( ans2x && ans2y && ans2x != j && ans2y != i && ans2x != j && ans2y != i + 1 ){
printf( "-1\n" );
exit(0);
}
else{
flag = 1;
if( k[j][i] && k[j][i+1] ){
printf( "-1\n" );
exit( 0 );
}
else if( k[j][i] )
ans2x = j , ans2y = i;
else if( k[j][i+1] )
ans2x = j , ans2y = i+1;
k[j][i] ++ , k[j][i+1] ++;
}
break;
}
else if( (a[j][i] ^ a[j][i+1] ) == 1 && cnt1 == 1 ){
if( ans2x && ans2y && ans2x != j && ans2y != i && ans2x != j && ans2y != i + 1 ){
printf( "-1\n" );
exit(0);
}
else{
//flag = 1;
if( k[j][i] && k[j][i+1] ){
printf( "-1\n" );
exit( 0 );
}
else if( k[j][i] )
ans2x = j , ans2y = i;
else if( k[j][i+1] )
ans2x = j , ans2y = i+1;
k[j][i] ++ , k[j][i+1] ++;
}
break;
}
}
}
if( (ans1x != ans2x || ans1y != ans2y ) && ( ans1x && ans2x ) )//最后有可能整个图只能变为全部一样,那么也要输出-1
printf( "-1\n" );
else if( ans1x )
printf( "%d %d\n" , ans1x , ans1y );
else if( ans2x )
printf( "%d %d\n" , ans2x , ans2y );
else
printf( "-1\n" );
return 0;
} 然后是老师的方法:
我们先将最后一行的所有点变为一样的L(或R),然后在一行行扫。
统计一行的L与R的字符个数
如果找到一行某个字符个数为1(L,R都可以),那么这个点就是答案
如果某字符个数为2,那么就是说无论怎样对这一行进行翻转,不可能只有一个点与其他点不同,因为列是不能转的,已经把最后一行变为一样了,如果再变列,就会破坏一样的
如果找到答案,那么以后的行就必须全都相同,否则有-1
#include
#include
#include
#include
#include
using namespace std;
int n , a[1003][1003];
int main()
{
scanf( "%d" , &n );
for( int i = 1 ;i <= n ; i ++ ){
for( int j = 1 ; j <= n ; j ++ ){
char c;
cin>>c;
if( c == 'R' )
a[i][j] = 0 ;
else
a[i][j] = 1;
}
}
for( int i = 1 ; i <= n ; i ++ ){
if( a[n][i] == 0 )
for( int j = 1 ; j <= n ; j ++ )
a[j][i] = !a[j][i];
}
bool flag = 0;
int ans0 = 0 , ans1 = 0;
for( int i= 1 ; i <= n ; i ++ ){
int cnt0 = 0 , cnt1 = 0;
for( int j = 1 ; j <= n ; j ++ ){
if( !a[i][j] ) cnt0 ++;
else cnt1++;
}
if( cnt0 >= 2 && cnt1 >= 2 ){
printf( "-1" );
exit( 0 );
}
if( ( cnt0 == 1 || cnt1 == 1 ) && flag ){
printf( "-1" );
exit( 0 );
}
if( ( cnt0 == 0 && cnt1 == n ) || ( cnt0 == n && cnt1 == 0 ) )
continue;
for( int j = 1 ; j <= n ; j ++ ){
if( a[i][j] && cnt1 == 1 ){
ans0 = i , ans1= j;
flag = 1;
break;
}
else if( !a[i][j] && cnt0 == 1 ){
ans0 = i , ans1= j;
flag = 1;
break;
}
}
}
if( !ans0 ){
printf( "-1" );
return 0;
}
printf( "%d %d" , ans0 , ans1 );
return 0;
}
总结一下这道题的做法,第二种是一个模板的思路,就是先确定一行,然后再一个个往上确定
而都有一个共同点,就是先封锁了列的操作,使其没有用或者不能用,然后就可以确定更容易
2.[USACO19OPEN]Cow Steeplechase II
这是提高组的题??
要用到扫描线的思想加STL+计算几何
在过去,Farmer John曾经构思了许多新式奶牛运动项目的点子,其中就包括奶牛障碍赛,是奶牛们在赛道上跑越障碍栏架的竞速项目。他之前对推广这项运动做出的努力结果喜忧参半,所以他希望在他的农场上建造一个更大的奶牛障碍赛的场地,试着让这项运动更加普及。
Farmer John为新场地精心设计了 NN 个障碍栏架,编号为 1 \ldots N1…N ( 2 \leq N \leq 10^52≤N≤105 ),每一个栏架都可以用这一场地的二维地图中的一条线段来表示。这些线段本应两两不相交,包括端点位置。
不幸的是,Farmer John在绘制场地地图的时候不够仔细,现在发现线段之间出现了交点。然而,他同时注意到只要移除一条线段,这张地图就可以恢复到预期没有相交线段的状态(包括端点位置)。
请求出Farmer John为了恢复没有线段相交这一属性所需要从他的计划中删去的一条线段。如果有多条线段移除后均可满足条件,请输出在输入中出现最早的线段的序号。
输入格式
输入的第一行包含 NN 。余下 NN 行每行用四个整数 x_1,y_1,x_2,y_2x1,y1,x2,y2 表示一条线段,均为至多 10^9109 的非负整数。这条线段的端点为 (x_1,y_1)(x1,y1) 和 (x_2,y_2)(x2,y2) 。所有线段的端点各不相同。
输出格式
输出在输入中出现最早的移除之后可以使得余下线段各不相交的线段序号。
输入输出样例
输入 #1复制
4
2 1 6 1
4 0 1 5
5 6 5 5
2 7 1 3输出 #1复制
2说明/提示
注意:由于线段端点坐标数值的大小,在这个问题中你可能需要考虑整数类型溢出的情况。
其实这道题就是要算到两条线段相交,那么答案就一定在两条线段中,暴力跑一遍判断即可
那么怎么求相交,且序号最先呢?
把每个点x坐标从小到大排序,相等情况y坐标从小到大
然后把每一个点装入set中
如果这是一个左端点(就是较小的那个点),则就看它的左右是否与它相交
否则如果是右端点,那么就看他的左右是否相交,然后删除这条线段
经过一系列操作后,就可以得出这道题的答案了
那么还有一个问题,怎么求相交?
有一个简单的方法:
求解析式,联立,合并,再看交点是否在线段上
当然,这样的方法是不完善的
我们需要用到:对立叉乘试验
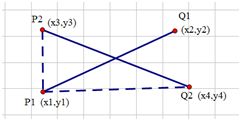
也就是对于两条线段
将其这样连线,然后算P2,P1与Q1,P1的叉乘,如果他们的符号相同,说明就是按上图这样排列的,但是还要判断一次
至于set里面的顺序,是这样排序的
把这条线段与扫描线相交的点的y坐标从小到大排序
这样只用判断上下两边是否相等即可
#include
#include
#include
#include
#include
using namespace std;
#define ll long long
int n;
double x;
struct node{
ll x , y ;
int num;
};
struct sege{
node s , l ;
int numb;
}q;
bool operator < ( node a , node b ){
if( a.x == b.x )
return a.y< b.y;
return a.x < b.x;
}
int check( ll x ){
if( x == 0 )
return 0;
if( x > 0 )
return 1;
return -1;
}
int operator * ( node a , node b ){
return check( b.y * a.x - b.x * a.y );
}
node operator - ( node a , node b ){
node no;
no.x = a.x - b.x, no.y = a.y - b.y;
return no;
}
bool cc( sege a , sege b ){
node p1 = a.s , q1 = a.l , p2 = b.s , q2 = b.l;
return ( ( ( q2 - p1 ) * ( q1 - p1 ) ) * ( ( q1 - p1 ) * ( p2 - p1 ) ) >= 0) && ((q1-p2)*(q2-p2)) * ((q2-p2)*(p1-p2)) >= 0;
}
double smx( sege s ){
if( s.l.x == s.s.x ) return s.s.y;
return s.s.y + ( s.l.y - s.s.y) * ( x - s.s.x ) / ( s.l.x - s.s.x );
}
bool operator < ( sege a , sege b ){
return a.numb != b.numb && smx( a ) < smx( b );
}
bool operator ==( sege a, sege b ){
return a.numb == b.numb;
}
//bool operator < ( sege a , )
vectorP;
vectorG;
setse;
int main(){
scanf( "%d" , &n );
for( int i =0 ; i < n ; i ++ ){
scanf( "%lld%lld%lld%lld" , &q.s.x , &q.s.y , &q.l.x , &q.l.y );
q.numb = q.l.num = q.s.num = i;
P.push_back( q );
G.push_back( q.l ) , G.push_back( q.s );
}
sort( G.begin() , G.end());
int ans1 , ans2;
for( int i = 0 ; i < n * 2 ; i ++ ){
ans1 = G[i].num;x = G[i].x;
set::iterator it = se.find( P[ans1] );
if( it != se.end() ){
set::iterator last = it , start = it ; last ++;
if( last != se.end() && start != se.begin() ){
start --;
if( cc( P[start->numb] , P[last->numb] ) ){
ans1 = start->numb , ans2 = last->numb;
break;
}
}
se.erase( it );
}
else{
set::iterator it = se.lower_bound( P[ans1] );
if( it != se.end() ){
if( cc( P[it->numb] , P[ans1]) ){
ans2 = it->numb;
break;
}
}
if( it != se.begin() ){
it --;
if( cc( P[it->numb] , P[ans1] ) ){
ans2 = it->numb;
break;
}
}
se.insert( P[ans1] );
}
}
//printf( "%d %d\n" , ans1 , ans2 );
bool flag = 0;
for( int i = 0 ; i < n ; i ++ ){
if( i != ans1 && i != ans2 ){
if( cc( P[i] , P[ans1] ) ){
flag = 1;
break;
}
}
}
if( flag )
printf( "%d" , ans1 + 1 );
else
printf( "%d" , min( ans1 , ans2 ) + 1 );
}
3.三角形
题目描述
平面上有n行m列,一共n*m个方格,从上到下依次标记为第1,2,...,n行,从左到右依次标记为第1,2,...,m列,方便起见,我们称第i行第j列的方格为(i,j)。小Q在方格中填满了数字,每个格子中都恰好有一个整数a_{i,j}。小Q不 喜欢手算,因此每当他不想计算时,他就会让你帮忙计算。小Q一共会给出q个询问,每次给定一个方格(x,y)和一个整数k(1<=k<=min(x,y)),你需要回答由(x,y),(x-k+1,y),(x,y-k+1)三个格子构成的三角形边上以及内部的所有格子的a的和。
输入格式
第一行包含6个正整数n,m,q,A,B,C(1<=n,m<=3000,1<=q<=3000000,1<=A,B,C<=1000000) 其中n,m表示方格纸的尺寸,q表示询问个数。 为了防止输入数据过大,a和询问将由以下代码生成:
unsigned int A,B,C;
inline unsigned int rng61(){
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main(){
scanf("%d%d%d%u%u%u", &n, &m, &q, &A, &B, &C);
for(i = 1; i <= n; i++)
for(j = 1; j <= m; j++)
a[i][j] = rng61();
for(i = 1; i <= q; i++){
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min(x, y) + 1;
}
}
输出格式
为了防止输出数据过大,设f_i表示第i个询问的答案,则你需要输出一行一个整数,即:
题目描述
平面上有n行m列,一共n*m个方格,从上到下依次标记为第1,2,...,n行,从左到右依次标记为第1,2,...,m列,方便起见,我们称第i行第j列的方格为(i,j)。小Q在方格中填满了数字,每个格子中都恰好有一个整数a_{i,j}。小Q不 喜欢手算,因此每当他不想计算时,他就会让你帮忙计算。小Q一共会给出q个询问,每次给定一个方格(x,y)和一个整数k(1<=k<=min(x,y)),你需要回答由(x,y),(x-k+1,y),(x,y-k+1)三个格子构成的三角形边上以及内部的所有格子的a的和。
输入格式
第一行包含6个正整数n,m,q,A,B,C(1<=n,m<=3000,1<=q<=3000000,1<=A,B,C<=1000000) 其中n,m表示方格纸的尺寸,q表示询问个数。 为了防止输入数据过大,a和询问将由以下代码生成:
unsigned int A,B,C;
inline unsigned int rng61(){
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
int main(){
scanf("%d%d%d%u%u%u", &n, &m, &q, &A, &B, &C);
for(i = 1; i <= n; i++)
for(j = 1; j <= m; j++)
a[i][j] = rng61();
for(i = 1; i <= q; i++){
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min(x, y) + 1;
}
}
输出格式
为了防止输出数据过大,设f_i表示第i个询问的答案,则你需要输出一行一个整数,即:
样例
输入样例
3 4 5 2 3 7
输出样例
3350931807
样例
输入样例
3 4 5 2 3 7
输出样例
3350931807
这道题输入有点奇怪
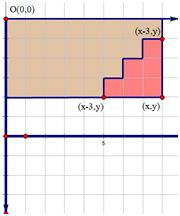
讲正解,不难发现这是一个直角三角形,且如果变为方格就成了阶梯形
那么用大矩形减去这个阶梯形前缀和就可以了。
阶梯形矩形前缀和这样维护
for( int i = 1; i<= n; i++){
for( int j = 1; j <= m; j++){
sum[i][j] = rng61();
ll x = sum[i][j];
sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + sum[i][j];
sumh[i][j] = sumh[i][j-1] + x;sum2[i][j] = sum2[i-1][j+1] + sumh[i][j];
}
sum2[i][0] = sum2[i-1][1];
}注意sum2[i][0]的用法,第i行为0,则第i-1行就有一个,递推可得
那么这道题就直接减即可
对吗????
不一定对。因为如果上图的三角形向下移动一个,那么明显第二行的棕色格子就会占满,也就是说这个图应该是大矩形减去以三角形顶角为末尾的矩形再减去棕色部分
那么现在的阶梯状棕色部分怎么求呢如果按照我写的变量,就是sum2[i-k][j] - sum2[i][j-k]注意这里阶梯状可能会延伸。
如果上图的(0,0)向左上方延伸,那么直接用sum2[i-k][j]减就会发现多减了
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN =3003;
#define ll unsigned int
unsigned int A,B,C,x,y,k;
ll d[3000003];
int n , m , q;
inline unsigned int rng61(){
A ^= A << 16;
A ^= A >> 5;
A ^= A << 1;
unsigned int t = A;
A = B;
B = C;
C ^= t ^ A;
return C;
}
ll sum[3003][3003] , sum2[MAXN][MAXN] , sumh[MAXN][MAXN];
ll min_( ll x , ll y ){
if( x < y )
return x;
return y;
}
int main(){
scanf("%d%d%d%u%u%u", &n, &m, &q, &A, &B, &C);
for( int i = 1; i<= n; i++){
for( int j = 1; j <= m; j++){
sum[i][j] = rng61();
ll x = sum[i][j];
sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + sum[i][j];
sumh[i][j] = sumh[i][j-1] + x;sum2[i][j] = sum2[i-1][j+1] + sumh[i][j];
}
sum2[i][0] = sum2[i-1][1];
}
d[0] = 1;
for( int i = 1 ; i <= q ; i ++ )
d[i] = d[i-1] * 233;
ll ans = 0;
for( int i = 1; i<= q; i++){
x = rng61() % n + 1;
y = rng61() % m + 1;
k = rng61() % min_(x, y) + 1;
ll tot = d[q-i] * ( sum[x][y] - sum[x-k][y] - (sum2[x][y-k] - sum2[x-k][y] ) ) ;
ans = ans + tot;
}
printf( "%u\n" , ans );
return 0;
}
二.总结
考试考炸了
虽然用到了一点超纲的东西,但是其它的题不应该是这样
老师说到了检查的问题,有:
tips:最后十分钟检查
1.眼查
2.用小数据测试
3.生成极限数据
4.暴力对拍
检查是很重要的,自己一定要落实。
以后每道题(包括练习题)都要进行这样的检查,要养成习惯!!!
同时,自己的考试方法也有一定的问题:
在时间分配上做得不好
每次考试先通看题目,然后在选择做题。
题目的关键字要把握清楚,就是读题要细心