每日一题 Day3--leetcode53--最大子序和
每日一题 Day3–leetcode53–最大子序和
题目
链接:https://leetcode-cn.com/problems/maximum-subarray/
链接为leetcode中文社区,题目没有区别,感觉很好用
题面描述: 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
解析+c语言实现:
暴力求解
最容易想到的暴力解法与Day2无重复字符的最长子串类似,从左到右遍历求出以每一个数字为首的各个子序和,再找到最大。
int maxSubArray(int* nums, int numsSize){
int i,j;
int max=nums[0];
for(i=0;i<numsSize;i++)//从左到右遍历以第i个数字为首的子序
{
int temp=0;//每次i改变时temp清零
for(j=i;j<numsSize;j++)//j从i到最后遍历
{
temp+=nums[j];
max=max>temp?max:temp;//找过程中最大的值
}
}
return max;
}
运行结果:
 可以分析得到暴力解法由于循环套循环,所以是O(n2)复杂度,耗时368ms
可以分析得到暴力解法由于循环套循环,所以是O(n2)复杂度,耗时368ms
动态规划(DP)
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
上段描述来自百度百科,简单来说,动态规划即在状态变化时做出决策。一般动态规划问题可以划分为若干子问题,再在子问题的结果中做出决策,选择最优解,而子问题又可以划分为子子问题,想法类似于递归,与递归不同的是,动态规划问题会记录每次的状态,这样可以大大减少时间复杂度。
一般解决动态规划问题需要四步:
- 将问题划分为子问题
例如求一个数组n个数中最大的值便可以先求前n-1个数中最大值再与最后的值比较。 - 确定状态
例如数组的前n项中n便是一种状态,这种状态可以改变 - 确定边界条件
例如最前和最后项便是边界条件 - 确定状态转移方程
状态转移方程是dp问题中最重要的部分,它规定了状态dp(n)是怎么由dp(n-1)得到。
来分析本问题:
- 将问题划分为子问题
本问题想求数组n个数的最大子序和,便可以分解为先求以第n-1个数为结尾的最大子序和,再考虑加不加上第n项,而求第n-1数为结尾的和便可以先求第n-2为结尾的值,以此套娃递归…… - 确定状态
以第n项结尾的最大子序和中第n项便是状态 - 确定边界条件
以为是从后往前套娃,所以须要单独考虑第1项的处理 - 确定状态转移方程
dp(n)=max(dp(n-1)+nums[n],nums[n]);
当得到以第n-1项为结尾的最大子序和时,只需要考虑(这个最大子序+第n项后的和)与(第n项)之间比较大的那个便是以第n项为结尾的最大子序和。
注意!!: 本题结果不是刚刚求出来的以第n项为结尾的最大子序和,而是以第1项到第2项为结尾的最大子序和中最大的那一个,即过程中出现的最大值,原因:最大子序不一定包含第n项。
int maxSubArray(int* nums, int numsSize){
int dp[1000000];//dp状态
int i;
dp[0]=nums[0];//初始态
int max=nums[0];
for(i=1;i<numsSize;i++)
{
dp[i]=(dp[i-1]+nums[i])>nums[i]?(dp[i-1]+nums[i]):nums[i];
//状态转移方程
max=max>dp[i]?max:dp[i];//统计最大值
}
return max;
}
执行结果:
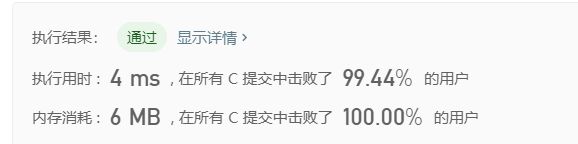
可以分析到,由于只有变量i进行了一次循环,dp方法的之间复杂度为O(n),也可以从时间上看出比较,从368ms到4ms,质的飞跃。
踩坑分享
天真的我一直以为leetcode的算法题不会卡数组空间的问题,所以最开始dp数组只开了100,直到我看到了这个测试用例↓(只截图了不到十分之一)

WA了一遍又一遍,又改为10000,又改为1000000,才解决问题,不过在这里夸一句leetcode在线编程的报错!精准有效!
贪心
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
以上描述又来自百度百科,简单来说,贪心问题就是每一步都选择最优解,这样最后便可以得到最优解。
但是! 不是所有问题都可以通过贪心来解决,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
dp与贪心的区别
本质上dp和贪心都是通过递推来解决问题,
而不同的是,贪心问题每一步做出的决策都无法改变,即这一步的最优解是由上一步的最优解所得到的而之前的最优解则不做保留。
而dp算法全局最优解中一定包含某个局部的最优解但不一定包含前一个局部的最优解,所以需要保存之前的所有最优解。
在此问题中,对于每一步的最优解即为(前面的和+nums[n])与nums[n]谁更大一些,如果前者更大其实便是第n项前的和为整数,如果后者便是为负数。
int maxSubArray(int* nums, int numsSize){
int sum=0;//记录和
int max=INT_MIN;
int i;
for(i=0;i<numsSize;i++)
{
sum+=nums[i];
max=max>sum?max:sum;//选择更大的
if(sum<0) sum=0;//如果为负数则置0
}
return max;
}
分治
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成。
上述描述同来自百度百科,简单来说,分治算法的思想为要解决一个问题,变可以分成三部分:将问题分为两部分,解决前一半,解决后一半,解决两部分之间的关系。
分析本题:
要得到n个数中的最大子序和,便可以将n个数分为两部分:
- 第1-n/2个数
- 第n/2+1-n个数
那么想得到的结果一定在这三部分中:
- 第一部分的最长子序和
- 第二部分的最长子序和
- 跨过两部分的最长子序和
而前两部分又可以继续划分下去,套娃真香
第三部分只需要类似于暴力解法从第n/2项向前和向后遍历找到最大子序和
最后找到三者中的最大值便是所求
int maxSubArray(int* nums, int numsSize){
return maxArray(nums,0,numsSize-1);
}
int maxArray(int *nums,int left,int right)/
{/套娃函数所需参数:数组和数组边界,left and right
if(left==right) return nums[left];//套娃结束条件
int mid=(left+right)/2;//取中间
int leftmax=maxArray(nums,left,mid);//第一部分
int rightmax=maxArray(nums,mid+1,right);//第二部分
int i,j;
int temp=nums[mid];
int midmax=nums[mid];//第三部分
for(i=mid-1;i>=left;i--)//遍历第n/2项左边
{
temp+=nums[i];
midmax=midmax>temp?midmax:temp;
}
temp=midmax;
for(i=mid+1;i<=right;i++)//遍历右边
{
temp+=nums[i];
midmax=midmax>temp?midmax:temp;
}
return maxABC(leftmax,rightmax,midmax);
}
int maxABC(int a,int b,int c)//手写的一个三个数取max
{
if(a<b)
a=b;
if(a<c)
a=c;
return a;
}
运行结果

可以分析得到,每次将问题分为两部分,这种分法需要进行logn次,而每次寻找包含第n/2项的最大子序和又需要遍历整个数组,为n的复杂度,所以此分治算法的时间复杂度为O(nlogn)
关于每日一题
疫情在家学业不重,又觉得自己算法很薄弱,所以希望可以每天刷一道算法题。
在翻leetcode找题的时候看到了推出的每日1题打卡计划,觉得不错,在此写下来加深记忆,也希望可以帮到其他人 。
今天只写了c语言实现,最近在学习python和go,在复习java,过几天尝试不同语言实现。
Day3总结:
leetcode53是一道简单的数组处理题,可以通过dp,贪心,分治,暴力各种思维来解决,在此可以感受到不同思维的优点和巧妙之处。
如果是刚刚接触dp,贪心和分治,可以用这道题作为很好的出发点,去理解不同的思维。
如果不出意外,每天这个时间更,欢迎监督,大家共勉。
欢迎关注公众号,日常同步博客内容,每日零点更新
![]()
