FP-growth:从FP树中挖掘频繁项集

前言

若想具体理解FP-growth，请参阅这位大神的作品：
https://www.cnblogs.com/pinard/p/6307064.html
本文的前一节《FP-growth：构建FP树》请点击：
https://blog.csdn.net/weixin_43901558/article/details/104320588

现在，我们已经有了这样一棵FP树，和头指针表：

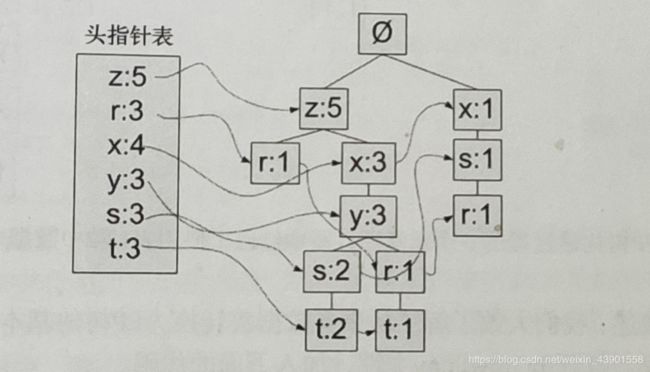
显而易见，我们已经找到了6个单元素项的频繁项（即头指针表中的六个元素）。接下来我们要做的是：以此为基础，构建多元素项的频繁项。

抽取条件模式基

其实，我觉得看书学习不太好的一点是，前面所学的概念，往往是在读到后面才知道他到底有什么作用。所以在学习过程中总是会一头雾水，只有在学完之后才会恍然大悟——那个地方原来是这么回事！
所以我想先把整个过程用大白话解释一遍，然后再讲具体流程。

现在，我们已经有了单元素项的频繁项，那我们怎么找双元素项的呢？
我的理解是：
以现在的FP树为基础，针对每个频繁的单元素项Ai，构建一个属于该元素的FP子树Bi。（想想为什么不用考虑FP树外的元素？）
我们也知道，FP树就是用来找频繁项的，那么Ai的FP子树的头节点表中都是相对Ai频繁的单元素项。Ai与这些单元素项的集合，不就是频繁的双元素项了吗？
那么怎么找三元素项呢？自然是构建双元素项的FP子树，再与该子树中的头节点表结合。以此类推，就会找到所有的多元素项。

那问题来了，怎么构建FP子树呢？这就要用到这里讲的条件模式基。
一个元素的条件模式基，就是指该元素的所有前缀路径的集合。
直接上例子吧，通过上图的FP树构造：

每一条前缀路径都与一个计数值关联，该数值等于起始元素项的计数值（比对着原FP树画一画？）

---

或许你会问了，FP子树和条件模式基又有什么关系呢？
在上一篇博客《FP-growth：构建FP树中》建树方法createTree一共有两个参数，一个是数据集，一个是最小支持度。而一个元素的条件模式基，就是该元素对应子树的数据集。

---

那怎么求得条件模式基呢？大致思想是：原FP树中的头节点表包含着该元素在树中第一次出现的结点指针，同时，结点的linknode属性中存储着下一个同元素结点的指针。一旦到达了每一个元素项，就可以上溯这棵树直到根结点为止。
代码如下：

# 上溯树，直到根节点
def ascendTree(leafNode, prefixPath):              
    if leafNode.parent is not None:
        prefixPath.append(leafNode.parent, prefixPath)
        ascendTree(leafNode.parent, prefixPath)


def findPrefixPath(basePat, treeNode):
    condPats = {}
    while treeNode is not None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        # 找到该元素在树中的下一个节点
        treeNode = treeNode.nodelink           
    return condPats

创建条件FP树

这里说的条件FP树也就是上文说的FP子树
对于每一个频繁项，都要创建一颗条件FP树（数据集为该频繁项的条件模式基），然后我们会递归地发现频繁项，再发现这些频繁项的条件模式基，再建立条件FP树…举个例子，为单元素频繁项t创建条件FP树，找到二元素频繁项{t,y}，{t,x}…再以这些二元素频繁项创建条件FP树，得到三元素频繁项
{t,x,y}…重复该过程，直到条件FP树中没有元素为止。
注意：对于一个频繁项A的条件FP树中的频繁项a，a的频繁不是指a的存在是否频繁，而是a相对A是否频繁
代码如下：

def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    # 从头指针表的底端开始
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p:p[1][0])]
    for basePat in bigL:
        newFreqSet = preFix.copy()
        # 头节点表中的元素add进原频繁项中
        newFreqSet.add(basePat)
        # 把更新后的频繁项添加到频繁项集freqItemList中
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        # 构建FP子树
        myCondTree, myHead = createTree(condPattBases, minSup)
        # 如果FP子树的头节点表不为空，即可再更新该频繁项
        if myHead is not None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

总代码

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue
        self.count = numOccur
        self.nodeLink = None
        self.parent = parentNode
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind=1):
        print(' ' * ind, self.name, self.count)
        for child in self.children.values():
            child.disp(ind+1)

# 传入的数据集其实是个字典，key值为事务， value值为数据集中该事务的频次
def createTree(dataSet, minSup=3):
    headerTable = {}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
            # 遍历数据集，构建headerTabel。其key为元素，value为元素出现频次
    for k in list(headerTable.keys()):
        # 如果元素频次小于最小支持度，则删去
        if headerTable[k] < minSup:
            del headerTable[k]
    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0:
        return None, None
    for k in headerTable:
        # 拓展头指针表，第二项存储着指向该元素在树中第一次出现位置的指针
        headerTable[k] = [headerTable[k], None]
        # 建一棵空树
    retTree = treeNode('Null Set', 1, None)
    for tranSet, count in dataSet.items():
        # localD存储过滤后的数据集
        localD = {}
        for item in tranSet:
            if item in freqItemSet:
                localD[item] = headerTable[item][0]
        if len(localD) > 0:
            # orderedItems存储过滤并重排序后的数据集
            orderedItems = [v[0] for v in sorted(localD.items(),
                                                key=lambda p: p[1], reverse=True)]
            updateTree(orderedItems, retTree,
                           headerTable, count)
    return retTree, headerTable


def updateTree(items, inTree, headerTable, count):
    # 如果第一个元素项作为子节点存在，则更新计数值
    if items[0] in inTree.children:
        inTree.children[items[0]].inc(count)
    else:
        # 否则创建一个新的子节点
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        # 如果在头指针表里该元素还没有指向的指针（即树上还没有出现该元素）
        if headerTable[items[0]][1] is None:
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1],
                         inTree.children[items[0]])
    # 如果事务中不止一个元素，则去掉第一个元素，再迭代
    if len(items) > 1:
        updateTree(items[1::], inTree.children[items[0]],
                                   headerTable, count)


def updateHeader(nodeToTeset, targetNode):
    while nodeToTeset.nodeLink is not None:
        nodeToTeset = nodeToTeset.nodeLink
    nodeToTeset.nodeLink = targetNode


def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat


def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict

# 上溯树，直到根节点
def ascendTree(leafNode, prefixPath):
    if leafNode.parent is not None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)


def findPrefixPath(basePat, treeNode):
    condPats = {}
    while treeNode is not None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        # 找到该元素在树中的下一个节点
        treeNode = treeNode.nodeLink
    return condPats


def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    # 从头指针表的底端开始
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p:p[1][0])]
    for basePat in bigL:
        newFreqSet = preFix.copy()
        # 头节点表中的元素add进原频繁项中
        newFreqSet.add(basePat)
        # 把更新后的频繁项添加到频繁项集freqItemList中
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        # 构建FP子树
        myCondTree, myHead = createTree(condPattBases, minSup)
        # 如果FP子树的头节点表不为空，即可再更新该频繁项
        if myHead is not None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

simpDat = loadSimpDat()
initSet = createInitSet(simpDat)
myFPtree, myHeaderTab = createTree(initSet, 3)
freqItems = []
mineTree(myFPtree, myHeaderTab, 3, set([]), freqItems)
print(freqItems)

输出为所有的频繁项，如下：

[{'r'}, {'t'}, {'x', 't'}, {'t', 'z'}, {'x', 't', 'z'}, {'s'}, 
{'x', 's'}, {'y'}, {'x', 'y'}, {'t', 'y'}, {'x', 't', 'y'}, 
{'z', 'y'}, {'x', 'z', 'y'}, {'z', 't', 'y'}, {'x', 'z', 't', 'y'},
{'x'}, {'x', 'z'}, {'z'}]

代码部分来自《机器学习实战》
参考资料：《机器学习实战》第12章