李宏毅机器学习（六）

本文基于《统计学习方法》和《机器学习实战所写》

一、决策树(decision tree)模型与学习

1. 定义

决策树是一种基本的分类与回归方法，呈现树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空
间上的条件概率分布。主要优点是模型具有可读性，分类速度快。决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。

2. 决策树模型

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node) 和有向边(directed edge)组成。结点有两种类型：内部结点(intermal node)和叶结点(leaf node)。内部结点表示一个特征或属性，叶结点表示一个类。

用决策树分类，从根结点开始，对实例的某一特征进行测试, 根据测试结果，将实例分配到其子结点。这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。

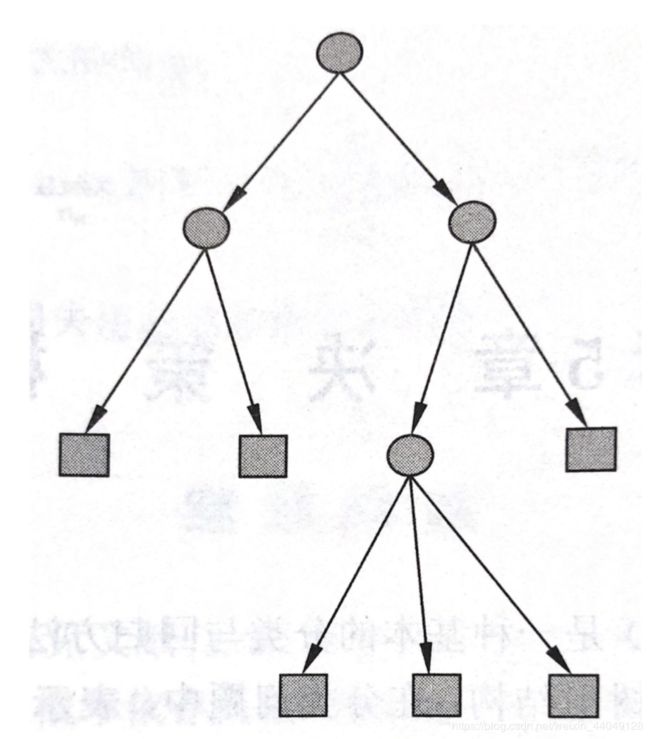
决策树模型。圆表示内部结点，方框表示叶节点。

3. 决策树递归

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

开始，构建根结点，将所有训练数据都放在根结点。选择一个最优特征，按照这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类，那么构建叶结点，并将这些子集分到所对应的叶结点中去；如果还有子集不能被基本正确分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的结点。如此递归地进行下去，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。最后每个子集都被分到叶结点上，即都有了明确的类。这就生成了一棵决策树。

二、特征选择

1. 定义

特征选择在于选取对训练数据具有分类能力的特征.这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的推则是信息增益或信息增益比。

2. 信息增益

1）定义

信息增益(information gain)表示得知特征$X$的信息而使得类$Y$的信息的不确定性减少的程度。（关于熵的相关知识可以看李宏毅机器学习(五)的内容）。特征$A$训练数据集D的信息増益$g(D,A)$，定义为集合$D$的经验熵$H(D)$与特征$A$给定条件下D的经验条件熵$H(D|A)$之差，即

$$g(D,A)=H(D)-H(D|A)\text{\hspace{1em}(2.1)}$$
一般地, 熵$H(Y)$与条件熵$H(Y|X)$之差称为互信息(mutual information)。

决策树学习中的信息增益等价于训练数据集中类与特征的互信息。决策树学习应用信息增益准则选择特征。给定训练数据集$D$和特征$A$，经验熵$H(D)$表示对数据集$D$进行分类的不确定性。而经验条件熵$H(D|A)$表示在特征$A$给定的条件下对数据集$D$进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征$A$而使得对数据集$D$的分类的不确定性减少的程度。

显然，对于数据集$D$而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力。根据信息增益准则的特征选择方法是：对训练数据集(或子集) $D$，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。

2）算法

设训练数据集为$D$，$|D|$表示其样本容量，即样本个数。设有$K$个类$C_k$, $k=1,2,\dots K$，$|C_k|$为属于类$C_k$的样本个数，${\sum }_{k=1}^K|C_k|=|D|$。设特征$A$有$n$个不同的取值$\{a_1,a_2,\dots ,a_n\}$,根据特征$A$的取值将$D$划分为$n$个子集$\{D_1,D_2,...,D_n\}$，$ |D_i|$为$D_i$的样本个数，$\sum_{i=1}^n|D_i|=|D|$。记子集$D_i$中属于类$C_k$的样本的集合为$D_{ik}$，即$D_{ik}=D_i\cap C_k$，$|D_{ik}|$为$D_{ik}$的样本个数。于是信息增益的算法如下:

输入：训练集D和特征A；输出：特征$A$对训练数据集$D$的信息增益$g(D,A)$。

(1) 计算数据集D的经验熵$H(D)$
$$H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}lo{g}_2\frac{|C_k|}{|D|}\text{\hspace{1em}(2.2)}$$
(2) 计算特征$A$对数据集$D$的经验条件熵$H(D|A)$
$$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum _{i=1}^n\frac{|D_i|}{|D|}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}lo{g}_2\frac{D_{ik}}{D_i}\text{\hspace{1em}(2.3)}$$
(3) 计算信息增益
$$g(D,A)=H(D)-H(D|A)\text{\hspace{1em}(2.4)}$$

3.信息增益比

信息增益值的大小是相对于训练数据集而言的，并没有绝对意义。在分类问题困难时，也就是说在训练数据集的经验熵大的时候，信息增益值会偏大。反之，信息增益值会偏小。使用信息增益比(information gain ratio)可以对这一问题进行校正。这是特征选择的另一准则。

信息增益比：特征$A$对训练数据集$D$的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集D的经验熵$H(D)$之比：
$$g_R(D,A)=\frac{g(D,A)}{H(D)}\text{\hspace{1em}(3.1)}$$

三、决策树的生成

主要介绍决策树学习的生成算法。

1. ID3算法

1）定义

ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树。

具体方法是：从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上方法，构建决策树。直到所有特征的信息增益均很小或没有特征可以选择为止，最后得到一个决策树。ID3 相当于用极大似然法进行概率模型的选择。

2）优点

1. 理论清晰，算法简单，很有实用价值的示例学习算法；
2. 计算时间是例子个数、特征属性个数、节点个数之积的线性函数，总预测准确率较令人满意。

3）缺点

1. 存在偏向问题，各特征属性的取值个数会影响互信息量的大小；
2. 特征属性间的相关性强调不够，是单变元算法；
3. 对噪声较为敏感，训练数据的轻微错误会导致结果的不同；
4. 结果随训练集记录个数的改变而不同，不便于进行渐进学习；
5. 生成的树容易产生过拟合。

2. C4.5的生成算法

1）定义

C4.5算法与ID3算法相似，C4.5 算法对ID3算法进行了改进。C4.5 在生成的过程中，用信息增益比来选择特征。

2）优点

1. 通过信息增益率选择分裂属性，克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足；
2. 能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理；
3. 构造决策树之后进行剪枝操作；
4. 能够处理具有缺失属性值的训练数据。

3）缺点

1. C4.5生成的是多叉树，即一个父节点可以有多个节点，因此算法的计算效率较低，特别是针对含有连续属性值的训练样本时表现的尤为突出。
2. 算法在选择分裂属性时没有考虑到条件属性间的相关性，只计算数据集中每一个条件属性与决策属性之间的期望信息，有可能影响到属性选择的正确性。
3. C4.5算法只适合于能够驻留内存的数据集，当训练集大得无法在内存容纳时，程序无法运行；

三、实战部分

1. 划分数据集

#!/usr/bin/env python
# -*- coding: utf-8 -*-
def splitDataSet(dataSet, axis, value):
    '''
    :param dataSet: 待划分的数据集
    :param axis: 划分数据集的特征
    :param value: 特征的返回值
    :return: 划分好的数据集
    '''
    retDataSet = []
    for featVec in dataSet:
    	# 程序将符合特征的数据抽取出来
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

简单理解这段代码：当我们按照某个特征划分数据集时，就需要将所有符合要求的元素抽取出来。其中两个方法需要注意：

1. extend()和append()方法

 >>> a=[1,2,3]
 >>> b=[4,5,6]
 >>> a.append(b)
 >>> a
 [1, 2, 3, [4, 5, 6]]

可见，如果执行a.append(b)，则列表得到了第四个元素，而且第四个元素也是一个列表。然而如果使用extend方法:

 >>> a=[1,2,3]
 >>> a.extend(b)
 >>> a
 [1, 2, 3, 4, 5, 6]

则得到一个包含a和b所有元素的列表。

2. 选择最好的数据集划分方式

该函数实现选取特征，划分数据集，计算得出最好的划分数据集的特征。

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    # 计算整个数据集的原始香农熵
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1

    # 遍历数据集中的所有特征
    for i in range(numFeatures):
    	# 将数据集中所有第i个特征值或者所有可能存在的值写入这个新list中
        featList = [example[i] for example in dataSet]
        # 使用set数据类型得到互不相同的元素值
        uniqueVals = set(featList)
        newEntropy = 0.0

        # 计算每种划分方式的信息熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy

        if (infoGain > bestInfoGain):
        	# 计算最好的信息增益
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

3.创建树的函数代码

def createTree(dataSet,labels):
	'''
	:param dataSet: 数据集
    :param labels: 标签列表
    :return: 决策树信息，字典类型
	'''
	# 创建列表包含数据集的所有类标签
    classList = [example[-1] for example in dataSet]

    # 若类别完全相同，则停止划分
    if classList.count(classList[0]) == len(classList): 
        return classList[0]

    # 数据集中没有其余特征，则停止划分    
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # 存储最好的特征
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}

    # 得到列表包含的所有属性值
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)

    # 遍历当前选择特征包含的所有属性值
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree