简明KPCA及其python实现（核主成分分析）

source：python machine learning 3rd

KPCA

核主成分分析-kernel principal component analysis，是一种用于非线性分类的降维工具，实现非线性映射降维

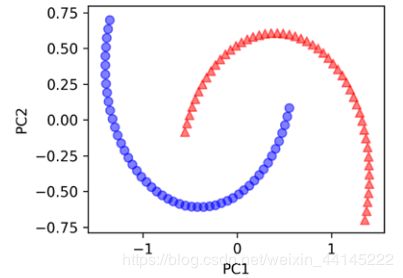
右图为典型的非线性分类问题

面对这样的分类问题，KPCA其实是先采用增加多项式等方式提高了数据的维度，再使用标准PCA，寻找一个可以进行有效分类的方向进行投影降维。

但是在进行PCA运算时，我们使用近似核心方程处理协方差矩阵，不再进行特征矩阵和特征值的计算（减少计算量），从而直接获得近似的投影后坐标，这与近似核心方程再SVM中的作用是一样的（不清楚背后的数学原理，考研时补好高数线代概率论再回来看吧。。。）

KPCA， PCA与LDA

• PCA：主要用于线性非监督学习（监督学习也可以）的数据降维
• LDA：主要用于线性监督学习的数据降维
• KPCA：得益于PCA非监督及监督学习通吃的特性，KPCA适用于几乎所有的非监督/监督非线性分类问题

核心方程

是否了解用于SVM非线性问题中的核心方程？这里的核心同样代表着使用核心方程实现非线性转换的意思，包括：

• 多项式核心: $$\kappa \left(x^{(i)},x^{(j)}\right)={\left(x^{(i{)}^T}{x}^{(j)}+\theta \right)}^p$$
• 双曲正切核心: $$\kappa \left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)=\tanh \left(\eta {\mathbf{x}}^{(i{)}^T}{\mathbf{x}}^{(j)}+\theta \right)$$
• 高斯核心(RBF): $$\kappa \left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)=\exp \left(-\frac{{\Vert {\mathbf{x}}^{(i)}-{\mathbf{x}}^{(j)}\Vert }^2}{2{\sigma }^2}\right)$$

RBF KPCA

高斯核心在SVM和KPCA中都是很常用很好用的核心方程。RBF KPCA的实现d–>k降维原理：

1. 使用高斯核心近似方程$$\kappa \left(x^{(i)},x^{(j)}\right)=\exp \left(-\gamma {\Vert x^{(i)}-x^{(j)}\Vert }^2\right)$$改造协方差矩阵来计算核心近似矩阵K：$$\mathbf{K}=\left[\begin{array}{cccc}\kappa \left({\mathbf{x}}^{(1)},{\mathbf{x}}^{(1)}\right)& \kappa \left({\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)}\right)& \cdots & \kappa \left({\mathbf{x}}^{(1)},{\mathbf{x}}^{(n)}\right)\\ \kappa \left({\mathbf{x}}^{(2)},{\mathbf{x}}^{(1)}\right)& \left({\mathbf{x}}^{(2)},{\mathbf{x}}^{(2)}\right)& \dots & \kappa \left({\mathbf{x}}^{(2)},{\mathbf{x}}^{(n)}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \kappa \left({\mathbf{x}}^{(n)},{\mathbf{x}}^{(1)}\right)& \kappa \left({\mathbf{x}}^{(n)},{\mathbf{x}}^{(2)}\right)& \cdots & \kappa \left({\mathbf{x}}^{(n)},{\mathbf{x}}^{(n)}\right)\end{array}\right]$$其中K维n x n矩阵，n为RBF KPCA训练样本量
2. 中心化近似核心矩阵K$${\mathbf{K}}^{\prime }=\mathbf{K}-1_{\mathbf{n}}\mathbf{K}-\mathbf{K}{1}_{\mathbf{n}}+1_{\mathbf{n}}\mathbf{K}{1}_{\mathbf{n}}$$其中$1_{\mathbf{n}}$是一个n x n举证，矩阵中的元素值都是1\n
3. 根据中心化近似核心矩阵K选择特征值最大的前k个特征矢量，这些特征矢量不是PCA特征矢量计算中的投影后的坐标轴，而就是完成投影降维后的投影点的坐标（为什么一定要完成中心化？）

python实现RBF KPCA

使用KPCA时最重要的一点就是其内置高斯近似方程参数gamma值，这个值是无法通过理论获得的，只能够通过实践尝试获得较优的gamma值，这里使用的gamma值是15

半月形数据集：

scikit learn实现

from sklearn.datasets import make_moons
from sklearn.decomposition import KernelPCA

# 获得半月形的数据集
X, y = make_moons(n_samples=100, random_state=123)

# 建立目标维度为2的RBF模型
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)

# 使用KPCA降低数据维度，直接获得投影后的坐标
X_skernpca = scikit_kpca.fit_transform(X)

# 数据可视化
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
plt.show()

没错，使用scikit learn实现PCA时实际上只需要建立模型和完成降维两步

结果：

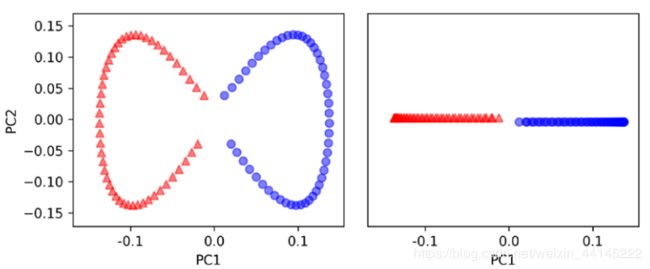
第一个图时使用KPCA进行坐标转换后的样本分布，第二个图为对PC1维度进行投影后的样本分布，我们可以很好地对其进行分类

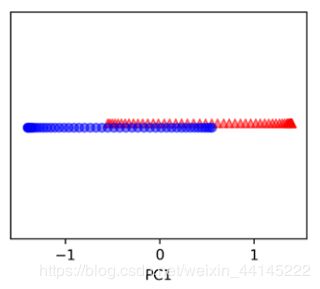
相比之下，使用PCA对最大方差正交轴进行投影后，结果不敬人意，相当一部分数据无法进行有效分类：

numpy + scipy实现

from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np

def rbf_kernel_pca(X, gamma, n_components):
    sq_dists = pdist(X, 'sqeuclidean')
    
    mat_sq_dists = squareform(sq_dists)
    
    K = exp(-gamma * mat_sq_dists)
    
    N = K.shape[0]
    one_n = np.ones((N, N)) / N
    K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
    
    eigvals, eigvecs = eigh(K)
    eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
    
    alphas =  np.column_stack([eigvecs[:, i] for i in range(n_components)])
    lambdas = [eigvals[i] for i in range(n_components)]
    
    return alphas, lambdas

使用：

alphas, lambdas = rbf_kernel_pca(X, gamma=15, n_components=1)

• alphas: 直接降维后获得的投影坐标，即是使用sklearn实现时的X_skernpca
• lambdas: 用于对新数据进行投影时的特征向量。我们知道KPCA与PCA最大的一个不同就是获得的矩阵即为投影后的坐标值而不是用于投影坐标转换的特征矩阵，无法对新的训练集数据进行转换处理，lambdas填补了这一缺陷