Q-learning学习的一个小例子
强化学习的难点,在于其引入了时间这个维度,不管是有监督还是无监督学习,都是能获得即使反馈,但到了强化学习中,反馈来的没那么及时。在周志华的《机器学习》中,举过一个种西瓜的例子。种瓜有很多步骤,例如选种,浇水,施肥,除草,杀虫这么多操作之后最终才能收获西瓜。但是,我们只有等到西瓜收获之后,才知道种的瓜好不好,也就是说,我们在种瓜过程中执行的某个操作时,并不能立即获得这个操作能不能获得好瓜,仅能得到一个当前的反馈,比如瓜苗看起来更健壮了。因此我们就需要多次种瓜,不断摸索,才能总结一个好的种瓜策略。
为了应对时间带来的不确定性,就需要一个框架来量化时间的流逝对我们关心奖励有怎样的影响。按照最简单的线性模型,我们首先确认要引入那些特征,首先是前一个时间的得分,其次是新发生的事件对奖励的影响,由于我们对未来的奖励看的不如现在的重要,因此可以引入折现率,折现率越高,说明我们越处于游戏的早期,对未来的关注也越多,这道理就如同我们在年轻时更要做长久的规划。同时在更新策略时,也会有快慢之分,将其称为学习率。由此得出了时间差分学习(Temporal Difference),简称TD方法的更新公式:

该公式描述了给定一个策略,该怎么去更新下一个时刻的估值函数,其中的V代表估值函数,下一个时刻的估值乘以折现率,再减去当前的差值,代表了一个策略的间接影响,可以看成是战略决策,再加上下一个时刻能立即获得的奖励,就是智能体(agent)应该关注的策略的影响,最后对此乘以学习率,用来控制随机性的影响,既要避免由于学习率过低导致的智能体学的太慢,也要避免学习率过高导致智能体矫枉过正。
由于在当下,你并不知道下一时刻的估值函数,所以你要做的是对其有一个尽可能准确的估算,这个估算被称为Q value,对应的算法称为Q-learning。如果你是用神经网络得出对未来value的估算的,那你使用的算法框架就从强化学习变为了深度强化学习。
下面是一个具体的例子,将一个结冰的湖看成是一个4×4的方格,每个格子可以是起始块(S),目标块(G)、冻结块(F)或者危险块(H),目标是通过上下左右的移动,找出能最快从起始块到目标块的最短路径来,同时避免走到危险块上,(走到危险块就意味着游戏结束)为了引入随机性的影响,还可以假设有风吹过,会随机的让你向一个方向漂移。
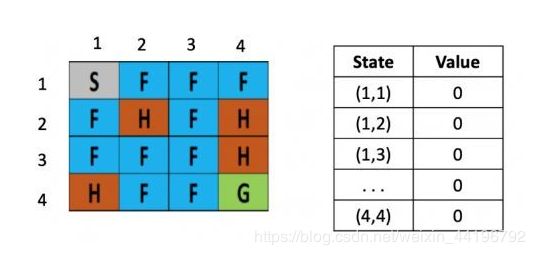
右图是每个位置对应的状态值的表,最初都是0,一开始的策略就是随机生成的,假定第一步是向右,那根据上文公式,假定学习率是0.1,折现率是0.5,而每走一步,会带来-0.4的奖励,那么(1,1)的value就是 0 + 0.1 ×[ -0.4 + 0.5× (0)-0] = -0.04,为了简化问题,此处这里没有假设湖面有风。
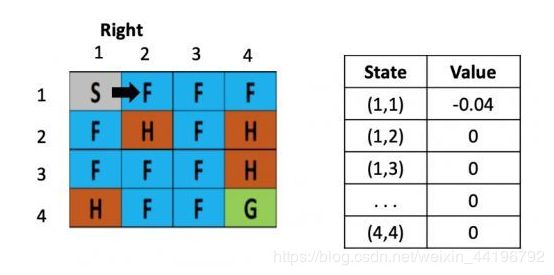
假设之后又接着往右走了一步,用类似的方法更新(1,2)的 value了,得到(1,2)的 value还为-0.04

等到了下个时刻,骰子告诉我们要往左走,此时就需要更新(1,3)的value,计算式为:V(s) = 0 +0.1× [ -0.4 + 0.5× (-0.04)-0) ]=-0.042
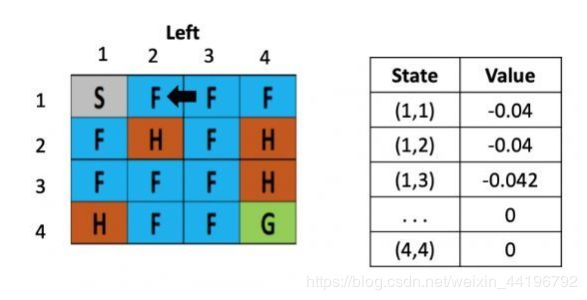
从这里,智能体就能学到先向右在向左不是一个好的策略,会浪费时间,依次类推,不断根据之前的状态更新表格,直到目标达成或游戏结束。这就是TD learning的基本步骤,通过多次的实验,智能体掌握了在不同位置下,相应的策略的估值分,从而解决了将较远的未来映射到当下的对不同策略的激励这个强化学习的核心问题。
根据是否亲自尝试不同的策略,TD可以分为在线和离线俩者,用学下棋来举例,前者是AI通过自己和人类选手下棋或者自我对弈来提升,而后者AI不操作只观察他人下棋的棋谱,下面看看再离线(off-line)的TD 中,value更新的公式又有了怎样的改变。
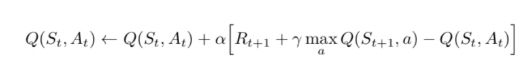
和之前的公式对比,最大的不同是未来的Q值是所有行动/策略对应的未来Q值中最大的那一个,这代表着模型根据已有的知识,选择了局部最优的那个行动,通过不断的优化Q table,使得这样一个只考虑一步的最简单型启发规则,也能学到全局相对较优的策略。
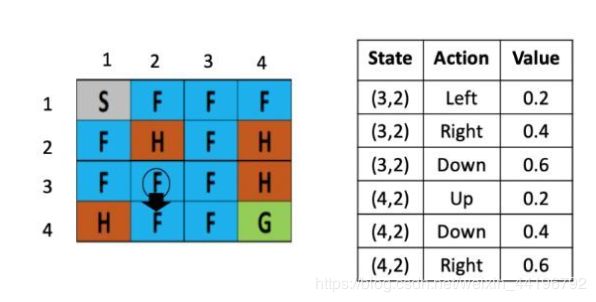
还是冰湖的案例,假设在训练的循环中,当前智能体已经学会了在(3,2)这个点上,向左和向右走对应的估值,此时模型要做的是去判定利用当前的知识,还是去探索未知策略的影响,探索是为了发现环境的更多信息,而当探索进行到了一定的程度,就需要根据已知信息去最大化奖励值,在Q learning中,通过一个0-1的参数来用随机性调控探索和利用的权衡。如图
假设骰子告诉智能体应该选择探索,因此选择了向下走,左图代表的之前智能体的Q-table,现在要做的是根据公式,更新(3,2)这里的Q value,由于向下走的Q-value最低,假定学习率是0.1,折现率是1,那么(3,2)这个点向下走这个策略的更新后的Q value就是:
Q( (3,2) down) = Q( (3,2) down ) + 0.1× (-0.4 + 1 × max [Q( (4,2) action) ]- Q( (3,2)down))
Q( (3,2), down) = 0.6 + 0.1× (-0.4 + 1 × max [0.2, 0.4, 0.6] – 0.6)=0.56
而在在线的TD算法下(称为State-Action-Reward-State-Action ,简称SARSA),Q table的更新公式变为了
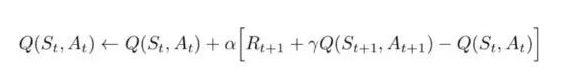
此处不同的是没有了max,由于是智能体在亲自参与,这里也就没法像离线时那样,选择一个最优的策略。不管是在线还是离线,在训练的时候需要做经验回放,即存储当前训练的状态到记忆体中,等下一次训练时再调用。
以上就是强化学习中最基础的TD,上诉的例子中不存在随机性,要引入随机性,可以需要通过蒙特卡罗的方法,来进行采样,同时引入对弈树,对其进行翦枝,这就是alpha zero的精髓。了解了Q learning的步骤,可以分析强化学习适用的领域所满足的假设,例如必须有能够清晰定义,事先已知且有限的策略,但现实生活中,真正重要的选择都是无限游戏,有无数种可能的选项,有前人根本不曾想到的选项,因此说强化学习不等价于强AI,只是通向强AI的一条必要选项。
不同于人类的学习,是首先对坏境建模,之后再根据模型找到合适的启发式规则,Q learning框架是模型无关的,不管是什么样的问题,Q learning做的都是去更新状态对应的估值表,不管问题本身具有什么样的特点。和人类思维的另一个不同是Q learning中没有因果关系,学到的Q table只是反映了奖励和策略之间的相关性,而人类的学习则是受着因果关系指引的。
Q-learning 算法:学习动作值函数(action value function)
动作值函数(或称「Q 函数」)有两个输入:「状态」和「动作」。它将返回在该状态下执行该动作的未来奖励期望。
我们可以把 Q 函数视为一个在 Q-table 上滚动的读取器,用于寻找与当前状态关联的行以及与动作关联的列。它会从相匹配的单元格中返回 Q 值。这就是未来奖励的期望。
在我们探索环境(environment)之前,Q-table 会给出相同的任意的设定值(大多数情况下是 0)。随着对环境的持续探索,这个 Q-table 会通过迭代地使用 Bellman 方程(动态规划方程)更新 Q(s,a) 来给出越来越好的近似。
Q-learning 算法流程

Q-learning 算法的伪代码
步骤 1:初始化 Q 值。我们构造了一个 m 列(m = 动作数 ),n 行(n = 状态数)的 Q-table,并将其中的值初始化为 0。

步骤 2:在整个生命周期中(或者直到训练被中止前),步骤 3 到步骤 5 会一直被重复,直到达到了最大的训练次数(由用户指定)或者手动中止训练。
步骤 3:选取一个动作。在基于当前的 Q 值估计得出的状态 s 下选择一个动作 a。
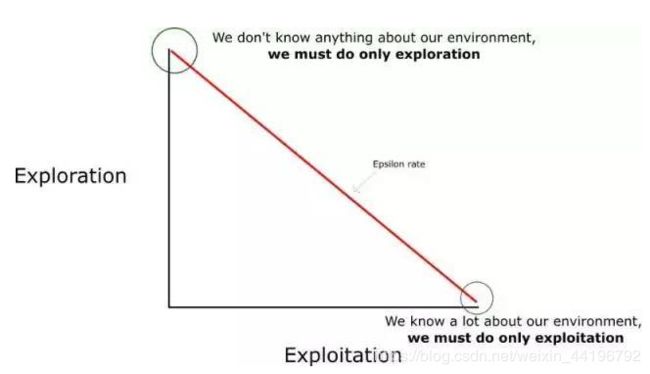
但是……如果每个 Q 值都等于零,我们一开始该选择什么动作呢?在这里,我们就可以看到探索/利用(exploration/exploitation)的权衡有多重要了。
思路就是,在一开始,我们将使用 epsilon 贪婪策略:
我们指定一个探索速率「epsilon」,一开始将它设定为 1。这个就是我们将随机采用的步长。在一开始,这个速率应该处于最大值,因为我们不知道 Q-table 中任何的值。这意味着,我们需要通过随机选择动作进行大量的探索。
生成一个随机数。如果这个数大于 epsilon,那么我们将会进行「利用」(这意味着我们在每一步利用已经知道的信息选择动作)。否则,我们将继续进行探索。
在刚开始训练 Q 函数时,我们必须有一个大的 epsilon。随着智能体对估算出的 Q 值更有把握,我们将逐渐减小 epsilon。
步骤 4-5:评价!采用动作 a 并且观察输出的状态 s’ 和奖励 r。现在我们更新函数 Q(s,a)。
我们采用在步骤 3 中选择的动作 a,然后执行这个动作会返回一个新的状态 s’ 和奖励 r。
接着我们使用 Bellman 方程去更新 Q(s,a):
如下方代码所示,更新 Q(state,action):
New Q value = Current Q value + lr * [Reward + discount_rate * (highest Q value between possible actions from the new state s’ ) — Current Q value ]
申明与感谢:直接将参考的原文链接附上http://www.sohu.com/a/306743524_314987
http://baijiahao.baidu.com/s?id=1597978859962737001&wfr=spider&for=pc