机器学习十大经典算法——一元线性回归（附python代码）

多努力就会有多特殊（neverforever）——仌

一、十大经典算法

1. 线性回归
2. 决策树
3. 随机森林
4. 逻辑回归
5. 支持向量机
6. 朴素贝叶斯
7. K近邻算法
8. K均值算法
9. 神经网络
10. 集成学习
其他算法请参考我的其他文章

二、了解线性回归

线性回归分为:一元线性回归和多元线性回归.很明显一元只有一个自变量,多元有多个自变量。拟合多元线性回归的时候,可以利用多项式回归或曲线回归。
一元线性回归：

代价函数（最小二乘法）：使误差平方和
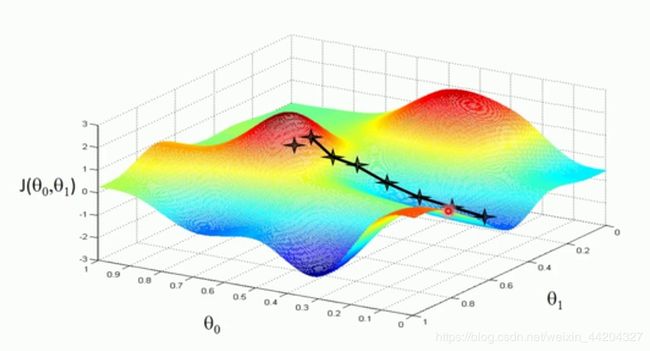
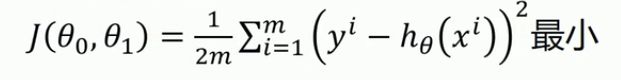线性回归的过程是：使用梯度下降算法是解决如何一步步调整参数，使代价函数达到最小值，从而确定参数θ0和θ1，则确定模型，梯度下降算法只适用凸函数。参数的结果与初始值的选取有极大关系，选不好容易陷入局部极小值，而不是全局最小值，一直求导求得代价函数的最小值。

三、python代码

'''
注：梯度下降算法的代价函数并不是随着迭代次数的增加而变小，而且代价函数（损失函数）的大小与初始值k，b，lr的选取有很大关系，
所以梯度下降算法只适用于代价函数为凸函数的情况。
'''
import numpy as np
import matplotlib.pyplot as plt
# 1. 导入数据（两列）
data=np.genfromtxt('\jupyter\data\Algorithm data\linear regression data.csv',delimiter=',')
x_data=data[:,0]   # 冒号前后：从第0行取到最后一行，逗号后面0：只要第一列
y_data=data[:,1]
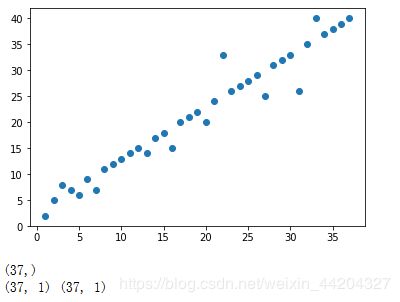
plt.scatter(x_data,y_data)  #  散点图
plt.show()
# 学习率learning rate（步长）、截距、斜率、最大迭代次数
lr=0.0005
b=1
k=0
epochs=5000
# 2. 代价函数（最小二乘法）:该函数只返回一个值
def compute_error(b,k,x_data,y_data):
    totalError=0
    for i in range(0,len(x_data)):
        totalError+=(y_data[i]-(k*x_data[i]+b))**2
    return totalError/float(len(x_data))
# 3. 梯度下降算法函数
def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
    # 总数据量
    m=float(len(x_data))
    # 迭代epochs次
    for i in range(epochs):
        b_grad=0
        k_grad=0
        for j in range(0,len(x_data)):
            b_grad+= -(1/m)*(y_data[j]-((k*x_data[j])+b))
            k_grad+= -(1/m)*x_data[j]*(y_data[j]-((k*x_data[j])+b))
        # 更新b和k
        b= b-(lr*b_grad)
        k= k-(lr*b_grad)
        # 每迭代500次，输出一次图像和数据
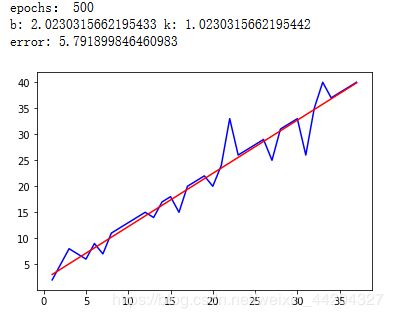
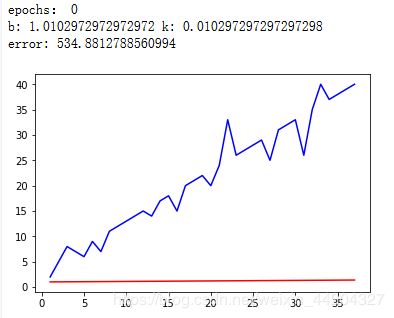
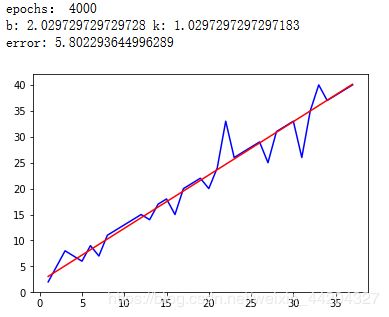
        if i%500 ==0:
            print('epochs：',i)
            print('b:',b,'k:',k)
            print('error:',compute_error(b,k,x_data,y_data),)
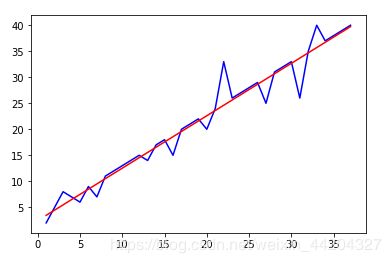
            plt.plot(x_data,y_data,'b')
            plt.plot(x_data,k*x_data+b,'r')
            plt.show()
    return b,k
gradient_descent_runner(x_data,y_data,b,k,lr,epochs)

data数据文件为两列（如图）：

四、方法二（调用sklearn库中LinearRegression模型）

# 使用sklearn完成一元线性回归
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 导入数据
data=np.genfromtxt('\jupyter\data\Algorithm data\linear regression data.csv',delimiter=',')
x_data=data[:,0]
y_data=data[:,1]
plt.scatter(x_data,y_data) 
plt.show()
print(x_data.shape)  # 数据格式（37,0）
# 转换数据格式为sklearn要求格式
x_data=data[:,0,np.newaxis]
y_data=data[:,1,np.newaxis]
print(x_data.shape,y_data.shape)  # sklearn 需要输入的数据格式（37，1）
# 创建并拟合模型
model=LinearRegression()
model.fit(x_data,y_data)
# 画图
plt.plot(x_data,y_data,'b')
plt.plot(x_data,model.predict(x_data),'r')
plt.show()

程序结果

五、总结

• 还没搞明白为什么梯度下降算法的代价函数并不是随着迭代次数的增加而变小，欢迎评论解答，多谢。
• data文件存放位置需要注意
• 代码中各小部分功能注释已经够详细了，希望能对你有所帮助。
• 程序调试遇到什么问题或有什么心得，可以加我微信863110979互相交流，空闲必回。