【论文阅读笔记】Gabor Convolutional Networks

Gabor Convolutional Networks

作者：Shangzhen Luan, Chen Chen , Baochang Zhang , Jungong Han，Jianzhuang Liu,

摘要

在可操纵的过滤器中，可以通过一组“基础滤波器”的线性组合生成任意方向的滤波器。然而，在深度卷积神经网络（DCNN）中尚未充分探索这些特性。因此，这篇文章提出一个新的深度模型，即Gabor卷积网络（GCN或Gabor CNN），将Gabor滤波器合并到DCNN中。

主要贡献

通过将Gabor滤波器合并到DCNN中，作者做出了如下四点贡献：

•这是将Gabor滤波器作为调制过程并入卷积滤波器的第一次尝试。 调制滤波器能够增强DCNN对图像变换（例如转换，比例变化和旋转）的鲁棒性。

•GoFs（Gabor orientation filters）可以很容易地整合到不同的网络架构中。

•由于Gabor滤波器具有预先定义的尺度和方向，GCN可以显著减少可学习滤波器的数量，使网络更紧凑，同时仍保持较高的特征表示能力。

•提供了在反向传播优化过程中更新Gabor方向滤波器的明确推导。

介绍

1、什么是Gabor

Gabor波由Gabor 发明，它使用复杂函数作为信息论应用中傅里叶变换的基础。 它的一个重要特性是其标准偏差的乘积在时域和频域都被最小化。 Gabor滤波器广泛用于模拟视觉皮层的简单细胞的接收区域。

2、问题的提出

图1.左图是AlexNet过滤器。 中间是Gabor过滤器。 右边是Gabor过滤器调制的卷积滤波器。

过滤器通常在CNN中冗余学习，其中一些类似于Gabor过滤器（带有黄色框的突出显示的过滤器）。 基于这种观察，作者提出 能否使用Gabor滤波器操纵学习卷积滤波器，以实现参数较少的滤波器的压缩深度模型？

Gabor Convolutional Networks

Gabor卷积网络（GCN）是使用Gabor定向滤波器（GoF）的深度卷积神经网络。 GoF是一个可操纵的滤波器，通过操纵Gabor滤波器组的学习卷积滤波器来创建，以产生增强的特征映射。 使用GoFs，GCN不仅可以减少更少的过滤器参数，还可以增强深层模型。

在下文中，将介绍在DCNN中实施GoF（Gabor orientation filter）的三个问题。

1、如何通过Gabor过滤器获取GoF？

图2.GoFs的调制过程

learned filters: 由标准CNN中的卷积滤波器通过反向传播（BP）算法学习获得。与标准CNN不同，为了对定向通道进行编码，GCN中的 learned filters 是三维的。将learned filters 的大小表示为N×W×W，其中W×W是滤波器的大小，N是指信道。为了在前向卷积过程期间保持特征图的通道数量一致，N要与Gabor滤波器的方向的数量保持一致。

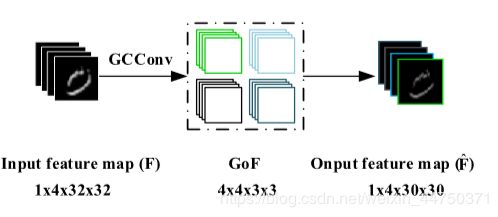
GoFs的调制过程： 如图2所示，learned filters 的大小是4x3x3，其中4表示定向通道数，3x3 表示滤波器的大小。Gabor filter bank 中有4个不同方向，大小均为3x3的Gabor滤波器。将learned filters与4个不同方向的Gabor滤波器进行逐元素相乘，就得到了GoF。

有关滤波器调制的详细信息如公式所示：

这里 $C_i{,}_o$ 表示 learned filter, $G(U,V)$ 表示一组Gabor滤波器，$。$表示 $G(U,V)$与每个2D滤波器之间的逐元素乘积运算。

2、 如何使用GoF来生成具有增强的比例和方向信息的特征图的卷积？

图3.具有4个通道的GCN卷积

如图所示，Input feature map 与GoF上四个方向的滤波器分别卷积，得到 Output feature map。

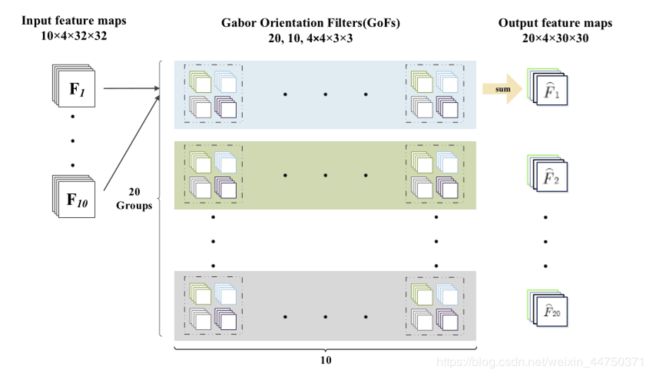
图4.具有多个特征映射的GCN的前向卷积过程。输入和输出分别有10组，20组特征图。 GoFs分为20组，每组包含10个GoF。

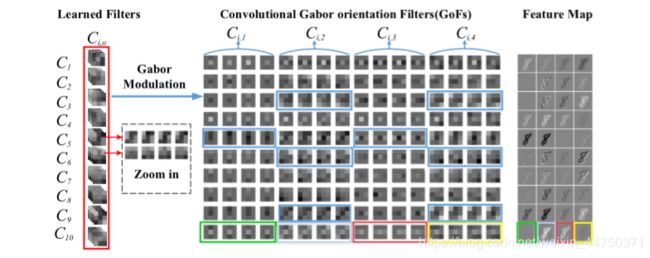
图5.可视化GCN的第一个卷积层

每行代表一组GoF及其相应的特征图。 即10个GoF（C10,1 … C10,4）。 每个4方向通道GoF标记为不同的颜色。 输出要素图还具有4方向通道，其标记颜色与其对应的GoF相同。 蓝色矩形中的表示GOF携带各种方向信息。

3、 在反向传播更新阶段如何学习GoF？

与传统的CNN不同，正向计算中涉及的权重是GCN中的GOF，但是保存的权重只是 learned filters的。 因此，在反向传播（BP）过程中，只需要更新learned filters。 我们需要总结GOF中子滤波器对应的学习滤波器的梯度：

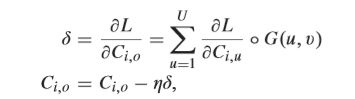
其中L是损失函数。 从上面的等式可以看出，BP过程很容易实现，并且与通常需要相对复杂的过程的ORN和可变形内核非常不同。 通过仅更新learned filters，GCNs模型更紧凑和有效，并且对于定向和尺度变化更加稳健。

实验

作者在 MNIST ，SVHN dataset , CIFAR-10 and CIFAR-100, ImageNet2012 ,
Food-101数据集上对GCNs的性能进行了验证。

1.MNIST

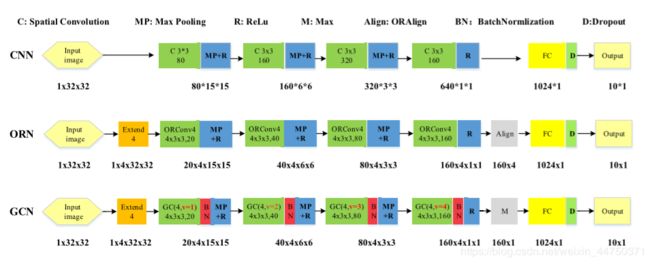
图5.CNNs,ORNs 和 GCNs的网络结构
通过图5所示结构，作者得出如下实验结果:

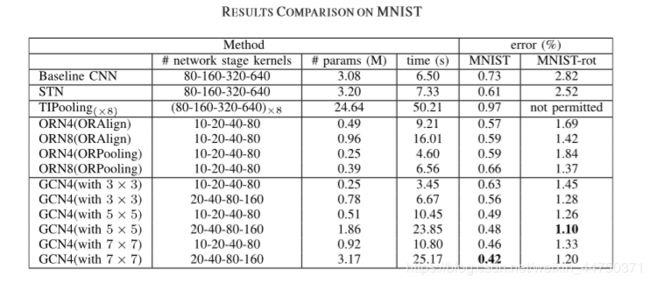
从图中第三列可知，与CNN相比，GCN需要的参数更少，复杂性降低；
从图中第四列可知，GCN训练时期的计算时间较短，比其他状态模型更有效。
从图中最后两列可知，与CNN进行比较，GCN在3x3内核中获得了更好的性能，但仅使用了CNN的1 / 12,1 / 4的参数。从实验中观察到，具有5x5和7x7核的GCN分别在MNIST-rot和MNIST上达到1.10％的测试误差，其优于ORN的测试误差。
这可以通过以下事实来解释：具有更大尺寸的内核携带更多Gabor方向的信息，从而捕获更好的方向响应特征。
图中还可以看出，更大的GCN模型可以带来更好的性能。此外，在MNIST-rot数据集上，CNN模型的性能受旋转的影响很大，而ORN和GCN可以捕获定向特征并获得更好的结果。同样，GCN优于ORN，这证实了Gabor调制确实有助于获得旋转变化的鲁棒性。

2.SVHN

对于这个大规模数据集，作者使用了基于ResNet的GCN。具体而言，用基于GoF的GCConv层替换空间卷积层，得到GCN-ResNet。由于1x1内核不传播任何Gabor滤波器信息，因此不使用此结构。具体如图所示：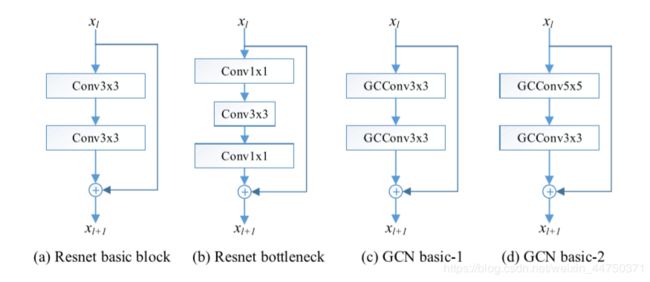
图6.（a）(b)表示Resnet的残差块，（b)（c）表示GCNs.
通过图5所示结构，作者得出如下实验结果:

实验结果表明，与其他网络结构相比，GCN可以在参数更少的情况下，取得更好的实验结果。

3.Natural Image Classification

对于自然图像分类任务，作者使用了CIFAR数据集，包括CIFAR-10和CIFAR-100 。与SVHN类似，在CIFAR数据集上测试GCN-ResNet。以将所提出的方法与最先进的网络（即NIN ，VGG ，ORN 和ResNet ）进行比较。
实验结果如下图所示：

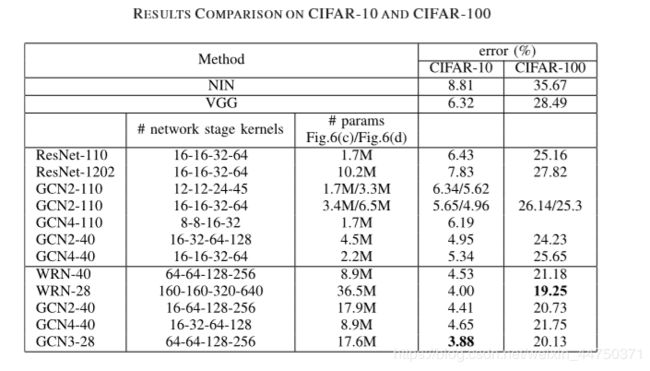
实验结果显示，与ResNet相比，无论参数或内核的数量如何，GCN都能始终如一地提高性能。我们进一步将GCN与宽残留网络（WRN）进行比较，当我们的模型是WRN的一半时，GCN再次获得更好的结果（3.88％对比4％的错误率）。

4.Large Size Image Classification

为了进一步显示所提出的GCNs方法的有效性，作者在ImageNet 数据集上对其进行了评估。与MNIST，SVHN和CIFAR不同，ImageNet拥有更高分辨率的图像。此外，图像通常每个图像包含多个属性，这可能对分类准确性产生很大影响。
实验结果如图所示：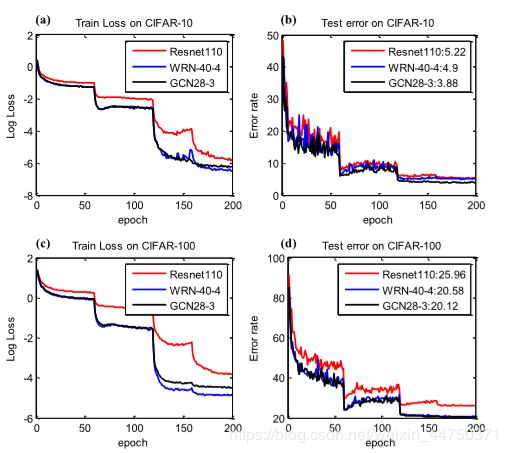
实验结显示，与基线ResNet-110相比，GCN实现了更快的收敛速度和更低的测试误差。 WRN和GCN实现了类似的性能，但GCN在测试集上的错误率较低。

5. Food-101 Dataset

基于具有更高分辨率的图像，收集Food-101数据集用于食物识别。通过与最先进的ResNets和内核池化方法进行比较，进一步验证GCNs的性能。

实验结果显示，我们的GCN在错误率方面比最先进KP方法实现了更好的性能。

小结

这篇通过将Gabor滤波器与DCNN相结合，提出了一种新的端到端深度模型，旨在通过可操纵的方向和比例来增强深度特征表示。所提出的Gabor卷积网络（GCN）通过在DCNN的卷积滤波器上引入额外的功能模块来改善DCNN的旋转和尺度变化的泛化能力，效果良好。