吴恩达|机器学习作业4.0神经网络反向传播（BP算法）

4.0.神经网络学习

1）题目：

在本练习中，您将实现神经网络的反向传播算法，并将其应用于手写数字识别任务。在之前的练习中，已经实现了神经网络的前馈传播，并使用Andrew Ng他们提供的权值来预测手写数字。在本练习中，将自己实现反向传播算法来学习神经网络的参数。
本次的数据与上次作业是一样的，这里不再赘述。
数据集链接: https://pan.baidu.com/s/1i_i77cVsa5TtdRCXAJVu6w 提取码: hdw6

2）知识点概括：

BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经各隐层逐层处理后，传向输出层。若输出层的实际输出与期望的输出(教师信号)不符，则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。权值不断调整的过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止。

• 神经网络通常的步骤：
  1）选择网络架构：即确定输入/输出层的神经元数量、隐层数目，输入/输出层的神经元数量通常由特征的维数和分类的类数所决定；
  2）训练网络：
  随机初始化权重；
  进行向前传播得到输出值；
  计算代价函数；
  反向传播计算参数偏导；
  梯度检查；
  使用最优化算法最小化代价函数。

• 前馈的过程在上次作业中已经梳理过了，即：
  

• Andrew Ng在讲误差反向传播的时候直接给出了误差的迭代公式，并没有说明具体过程，因此让我最开始除了不知所措以外还很难接受，所以我尝试了自己推导。
  

• 找了几本关于神经网络的书看了下，然后自己给出了一个4层的网络结构进行推导（主要参考书目：《人工神经网络教程》韩力群编著）
  
  
  这样就能得到误差迭代的公式。但是可以看出这里的公式和Andrew Ng给出的不一样，后来我才明白过来原来是因为这里的代价函数和Andrew Ng设置的代价函数不一样，这里的代价函数是所有误差的平方和，即$E=\frac{1}{2}\sum (h_{\theta }(x)-y{)}^2$，但是从这里明白了所谓“误差”，就是代价函数对权重求偏导，即$\frac{\partial }{\partial {\theta }_{ji}^{(l)}}J(\theta )$，并不是真正意义上的误差，而是表示了权重的微小变化对代价函数的影响。

• 所以很自然的就会想，那Andrew Ng给出代价函数是有意义的吗？然后首先回顾下逻辑回归代价函数的来历
  
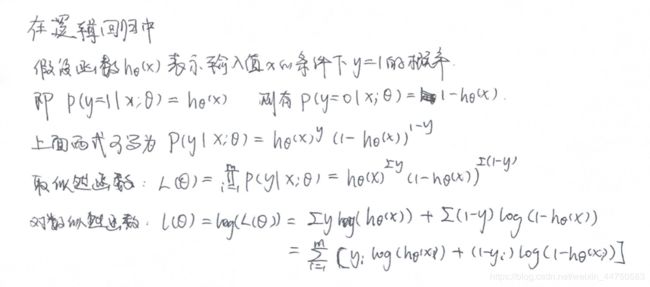
  求极大似然估计就是求参数的估计，使得所选取的样本在被选的总体中出现的可能性为最大，也就是最大化对数似然函数。最大化对数似然函数又等价于最小化$-\frac{1}{m}l(\theta )$，因此得到了逻辑回归的代价函数。
  神经网络的代价函数就是在这个基础上多了分类的类数，道理是一样的。在此基础上又增加约束惩罚参数，避免过拟合，最后才得到这个形式的代价函数：
  $J(\theta )=-\frac{1}{m}[{\sum }_{i=1}^m{\sum }_{k=1}^K{y}_k^{(i)}log(h_{\theta }(x^{(i)}){)}_k+(1-y_k^{(i)})log(1-(h_{\theta }(x^{(i)}){)}_k)]+\frac{\lambda }{2m}{\sum }_{l=1}^{L-1}{\sum }_{i=1}^{s_l}{\sum }_{j=1}^{s_{l+1}}({\theta }_{ji}^{(l)}{)}^2]$，所以结果就是这个代价函数本质上和误差的平方和是一样的。

• 所以我又按照Andrew Ng给出代价函数大概推了一下误差的迭代公式，可能下面有一些矩阵的乘法不是很严谨，大概意思是那样
  
  推出结果确实是按照Andrew Ng给出迭代公式完成的，因此理解上基本上就没有问题了，下一步就是执行了。

• 因为理解已经花费了大量的脑容量，所以很长一段时间没有弄明白这个算法究竟是要我干什么。其实很简单，我们的目标是最小化代价函数，也就是训练权重得到最小的代价函数，为了得到这个权重我们需要计算代价函数$J(\theta )$以及他对权重的梯度$\frac{\partial }{\partial {\theta }_{ji}^{(l)}}J(\theta )$，然后再把这两个值传给最优化函数fmin_ncg就可以得到训练好的权重了，也就是最小化了代价函数了。

• 梯度检验
  目的是保证在反向传播中没有bug。
  首先计算反向传播中的梯度向量。
  再采用双侧差分法，即在某点领域取一个很小的值，利用左右两点的连线来作为该点斜率的逼近$\frac{d}{d\theta }J(\theta )\approx \frac{J(\theta +ϵ)-J(\theta -ϵ)}{2ϵ}$，$ϵ$一般取为$10^{-4}$，当$\theta$是一个向量时，可以使其他${\theta }_j$保持不变，对每个${\theta }_i$分别进行双侧差分，而后得到数值上的梯度向量。
  最后将神经网络代价函数中所有参数的数值梯度向量与在反向传播中得到的梯度进行比较，看是否十分接近，这样能保证在进行反向传播时所计算的梯度是正确的。检查完之后禁用梯度检验函数以保证BP算法运行的空间节约训练时间。

• 随机初始化
  为解决对称权重问题，以防止对同一神经元的所有参数/权重都相等，需要随机地对初始的参数/权重赋值。一般说来初始化范围为，例如若随机生成的值属于，则只需即可。

• 对于可视化隐层的意义，我的理解是因为权重中每个值代表了对应输入神经元的权重，在这里就是一个数字的某个像素对下一层的影响有多大，如果某些像素值就是特别关键的可以识别出这个输入x是数字几的时候，那它们对应的权重自然就大，因此可以把隐层中的权重可视化可以看出隐层在尝试识别出一些笔画或者重要的图案。
  可以参考视频讲解更深理解神经网络的含义：https://www.bilibili.com/video/av16577449/?p=2

• 代价函数是非凸函数，因此最后的结果可能是局部极小值而不是全局最小值，但一般来说也是一个比较小的局部极小值。

3）大致步骤：

1. 读入数据，并随机选取100个样例进行数据可视化。
   模型展示，这里作业中给出了框架，即包含输入层、隐层和输出层的3层框架。神经元数量分别为400、25和10（不包含偏置单元）。
2. 将初始的标签向量y重新定义，展开成一个5000乘10的矩阵，每行只有对应标签的地方为1，其余为0，例如，对某一，表示的数字为4，即，则这一行展开为。
   参数展开，在这里需要提前将参数展开为一维的向量，因为在后面采用fmin_ncg函数训练参数时需要将theta的初始值赋予函数，这里的初始值要求是一维向量，因此在后面代价函数和梯度函数的定义中也要注意返回一维的梯度。
3. 代价函数，再计算未添加正则项的代价函数，注意这里代价函数以及后面的梯度函数都需要把第一个参数设为theta，也是因为fmin_ncg函数的需要。这里代价函数写完后，按照上次作业的前馈神经网络用给出的权重theta1和theta2计算出代价，检查一下代价是否为0.287629。然后再计算添加正则项的代价函数，同样检查代价是否为0.383770。
4. 误差逆向传播和梯度，首先计算不带正则项的梯度，然后再和不带正则项的数值梯度函数计算出来的值进行比较，如果两个向量差的二范数与向量和的二范数的比值的数量级小于等于e-09即可（梯度检验时要特别注意，因为很容易一点小错误就对不上了，如果有问题，可以看看梯度的第0项与数值梯度第0项的差，然后再一步步找，一般来说可能错的地方就在写BP函数以及调用函数的变量赋值过程中，这些都是我掉过的坑）。不带正则项的计算对了之后就开始写带正则项的梯度函数了，这里都没有按照吴恩达说的用for循环写，而是直接用矩阵计算，因此惩罚参数的时候只需把参数的第一列设为0然后加上之前的梯度就好了，写完之后依然是梯度检查，这里的数值梯度要用正则化的代价函数进行计算。注意计算数值梯度特别特别特别慢，因此在计算完之后就先注释掉吧，免得一不小心又跑了。。。
5. 训练权重并计算精度，先随机初始化参数（权重），然后使用牛顿共轭梯度法（opt.fmin_ncg函数）进行训练，这里也稍微有点慢，然后再用训练好的参数进行前馈传播得到预测的y值，再与期望的y值进行比较得出精度。
6. 最后可视化隐层，将训练好的参数的第一列去掉，即去掉偏置单元的权重，得到的向量代表每个样本输入到每个隐层单元的像素的权重。

4）关于Python：

np.concatenate函数可以合并矩阵，axis=0表示纵向相连。
np.random.uniform(-epsilon, epsilon, size)可以随机产生size大小的每个数取值为(-epsilon, epsilon)的矩阵。
注意opt.fmin_ncg的参数传递方式是第一个是theta，然后才是x和y等，因此它里面的代价函数和梯度函数的第一个值也要写成theta。

5）代码与结果：

这里代码比较长，放到最后面了，先放出结果来。

随机可视化部分x

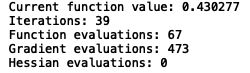
下面是随机初始化两次参数且lmd=1时的结果，可以看出迭代了39次可以看到精度比较高为96.96%，迭代了32次的精度比较低94.04%，这个和参数的随机初始化有关，作业上说大约为95.3%，相差1%都正常。后来把lmd改为0.1之后精度提高了很多（但过拟合风险高，也不太好）。

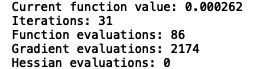
试了下无正则化的，结果精度100.00%，也就是说没有惩罚的出现了过拟合，估计要是能画出图的话边界曲线会很不光滑。也说明正则化对于缓解过拟合作用十分明显。

可视化隐层

全部代码如下：

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio #读取mat文件
import scipy.optimize as opt

data = scio.loadmat('ex4data1.mat')
weights = scio.loadmat('ex3weights.mat')
x = data['X']
y = data['y']
theta1 = weights['Theta1']
theta2 = weights['Theta2']

'''====================part1 前馈神经网络========================='''
'''数据可视化'''
s = np.random.permutation(x) #随机重排，但不打乱x中的顺序
a = s[:100,:] #选前100行,(100, 400)

#定义可视化函数
def displayData(x):
    plt.figure()
    n = np.round(np.sqrt(x.shape[0])).astype(int)
    #定义10*10的子画布
    fig, a = plt.subplots(nrows=n, ncols=n, sharex=True, sharey=True, figsize=(6, 6))
    #在每个子画布中画出一个数字
    for row in range(n):
        for column in range(n):
            a[row, column].imshow(x[n * row + column].reshape(20,20).T, cmap='gray')
    plt.xticks([]) #去掉坐标轴
    plt.yticks([])       
    plt.show()

displayData(a)


'''向前传播'''
#sigmoid函数作为激活函数
def g(x):
    return 1/(1+np.exp(-x))

#前面加一列1的函数
def plus1(x):
    return np.column_stack((np.ones(x.shape[0]), x))

#前馈函数
def forward_pro(x, theta1, theta2): #如果多层可添加theta
    b1 = x  #(5000, 400)
    for i in range(1,3): #如果为n层网络，则这里的3改为n即可
        locals()['a'+str(i)] = plus1(locals()['b'+str(i)])
        locals()['z'+str(i+1)] = locals()['a'+str(i)]@locals()['theta'+str(i)].T
        locals()['b'+str(i+1)] = g(locals()['z'+str(i+1)])
        if i+1 == 3:  #如果为n层网络，则这里的3改为n即可，这里添加这个命令主要是因为这里的值是暂时性的，for循环完就没了
            b3 = g(locals()['z'+str(i+1)])
    return b3  #(5000, 10)  如果为n层网络，这样输出也是an

#返回每层值的前馈函数，在计算反向传播时用到
def forward(x, theta1, theta2):
    a1 = plus1(x)
    z2 = a1@(theta1.T)
    a2 = plus1(g(z2))
    z3 = a2@(theta2.T)
    a3 = g(z3)
    return a1, z2, a2, z3, a3



'''代价函数'''
#把y向量化，对应类别的向量值为1，其余为0
def y_vec(y):
    y_vec = np.zeros((len(y), np.max(y))) #初始化生成一个(5000, 10)的零矩阵
    for i in range(len(y)):
        y_vec[i, y[i]-1] = 1 #对应类别的位置为1
    return y_vec

#展开参数的函数
def unrolling(x1, x2): #展开成 25*401+10*26=10285 维列向量
    return np.concatenate((np.reshape(x1, x1.size), np.reshape(x2, x2.size)), axis=0) #纵向相连
#重新组合，返回theta1和theta2
def reshapen(x):
    return np.reshape(x[0:10025], (25, 401)), np.reshape(x[10025:], (10, 26))

#不带正则化的代价函数
def nnCostFunc(theta, x, y):
    theta1, theta2 = reshapen(theta)
    prob = forward_pro(x, theta1, theta2)
    m = len(y)
    first_part = -np.multiply(y, np.log(prob)) - np.multiply((1-y), np.log(1-prob))    
    return np.sum(first_part)/m

#正则化的代价函数
def nnCostFunc_reg(theta, x, y, lmd=1):
    theta1, theta2 = reshapen(theta)
    m = len(y)
    cost = nnCostFunc(theta, x, y)
    reg = lmd/(2*m) * (np.sum(np.square(theta1[:, 1:])) + np.sum(np.square(theta2[:, 1:])))
    return cost+reg


#计算代价
y_vec = y_vec(y) 
theta = unrolling(theta1, theta2)
nnCostFunc(theta, x, y_vec) #0.287629
nnCostFunc_reg(theta, x, y_vec) #0.383769859


'''==========================part2 BP算法============================'''
#sigmoid函数的导数
def g_gradient(z):
    return g(z)*(1-g(z))

#随机初始化权重函数
def randIniWeights(size, epsilon):
    return np.random.uniform(-epsilon, epsilon, size)

'''梯度函数'''
#计算梯度
def BP(theta, x, y_vec):
    theta1, theta2 = reshapen(theta)
    a1, z2, a2, z3, a3 = forward(x, theta1, theta2)
    m = len(x)
    #计算误差
    delta3 = a3-y_vec #(5000,10)
    delta2 = delta3@theta2[:, 1:]*g_gradient(z2) #(5000,25)
    #更新梯度
    Delta2 = (delta3.T)@a2 #(10, 26)
    Delta1 = (delta2.T)@a1 #(25, 401)
    #展开梯度
    Delta = unrolling(Delta1, Delta2)
    return Delta/m


#正则化的梯度
def BP_reg(theta, x, y_vec, lmd=1):
    Delta = BP(theta, x, y_vec)
    theta1, theta2 = reshapen(theta)
    D1, D2 = reshapen(Delta)
    theta1[:, 0] = 0 #权重的第一列设为0，即不惩罚
    theta2[:, 0] = 0
    D1 = D1 + lmd/len(x)*theta1
    D2 = D2 + lmd/len(x)*theta2
    return unrolling(D1, D2)
    


'''梯度检查'''
#计算数值梯度的函数（不带正则项的）
def num_Gradient(x, y_vec, theta):
    numgrad = np.zeros(theta.shape)
    perturb = np.zeros(theta.shape)
    e = 1e-4
    for p in range(len(theta)):
        perturb[p] = e
        loss1 = nnCostFunc(theta - perturb, x, y_vec)
        loss2 = nnCostFunc(theta + perturb, x, y_vec)
        #计算数值梯度
        numgrad[p] = (loss2 - loss1) / (2*e)
        perturb[p] = 0
    return numgrad

'''谨慎运行！！！慢，至少五分钟
predict_gradient = BP(theta, x, y_vec) #(10285,)
num_gradient = num_Gradient(x, y_vec, theta) #(10285,)
#向量差的二范数与向量和的二范数的比值
diff = np.linalg.norm(num_gradient-predict_gradient)/np.linalg.norm(num_gradient+predict_gradient)
diff #数量级为e-09，这里结果为2.1448374139731396e-09
'''

#计算数值梯度的函数（正则约束）
def num_Gradient_reg(x, y_vec, theta):
    numgrad = np.zeros(theta.shape)
    perturb = np.zeros(theta.shape)
    e = 1e-4
    for p in range(len(theta)):
        perturb[p] = e
        loss1 = nnCostFunc_reg(theta - perturb, x, y_vec, lmd=1)
        loss2 = nnCostFunc_reg(theta + perturb, x, y_vec, lmd=1)
        #计算数值梯度
        numgrad[p] = (loss2 - loss1) / (2*e)
        perturb[p] = 0
    return numgrad

'''谨慎运行！！！太慢了
predict_gradient_reg = BP_reg(theta, x, y_vec, lmd=1) #(10285,)
num_gradient_reg = num_Gradient_reg(x, y_vec, theta) #(10285,)
diff_reg = np.linalg.norm(num_gradient_reg-predict_gradient_reg)/np.linalg.norm(num_gradient_reg+predict_gradient_reg)
diff_reg #数量级至少为e-09，这里结果为4.164180771263975e-10
'''


'''训练权重并评价'''
#随机初始化参数
theta0 = randIniWeights((10285,), 0.12)
#训练参数，也有点慢不过还好
result = opt.fmin_ncg(f=nnCostFunc_reg, fprime=BP_reg, x0=theta0, args=(x, y_vec, 1), maxiter=400)
#下面这个为不带正则项的
#result = opt.fmin_ncg(f=nnCostFunc, fprime=BP, x0=theta0, args=(x, y_vec), maxiter=400)


'''预测与评价'''
result1, result2 = reshapen(result)
prob_ = forward_pro(x, result1, result2) #用训练好的参数进行预测

#预测的y值
def predict(prob):
    y_predict = np.zeros((prob.shape[0],1))
    for i in range(prob.shape[0]):
        #查找第i行的最大值并返回它所在的位置,再加1就是对应的类别
        y_predict[i] = np.unravel_index(np.argmax(prob[i,:]), prob[i,:].shape)[0]+1
    return y_predict #返回(5000, 1)
        
#求精度，预测的y值与最初的期望y值进行比较
def accuracy(y_predict, y=y):
    m = y.size
    count = 0
    for i in range(y.shape[0]):
        if y_predict[i] == y[i]:
            j = 1 
        else:
            j = 0
        count = j+count #计数预测值和期望值相等的项
    return count/m

y_predict_ = predict(prob_)
print('accuracy = {:.2f}%'.format(accuracy(y_predict_)*100))   


'''==========================part3 可视化隐层============================'''
displayData(result1[:,1:])

最后还想吐槽下自己，做出来了觉得自己天下无敌，做不出来觉得自己一无是处，要拿什么拯救我的心态。。。