梯度下降法实现一元线性回归

 # 用于计算数据要用到的包numpy
 import numpy as np
 # 画图要用到的包matplotlib
 import matplotlib.pyplot as plt

 # 载入数据要用到numpy（由于项目和文件在同一个目录下，所以
 # 可以直接填写文件的名字就能加载文件，如果不是在同一个目录
 # 下，需要填写绝对路径；文件文件分隔符是“，”）
 data = np.genfromtxt("data.csv",delimiter= ",")
 
 # “ ：”在冒号的前后都不填任何信息，表示从第0行取到最后一行。
 # 逗号前表示取行，逗号后表示取列。 x_data表示取所有行的第1列，
 # 下标从0开始；y_data表示取所有行的第2列
 x_data = data[:,0]
 y_data = data[:,1]
 
 # 调用matplotlib包来画图。scatter表示画散点图
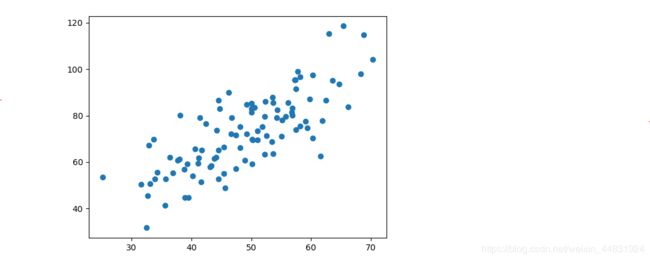
 plt.scatter(x_data,y_data)
 plt.show()

       最后画出来的散点图如下：

      这些点是数据集中的点，可以看到这些点大致成线性关系，所以我们要找到这条线，因此需要定义部分参数：学习率、斜率、最大迭代次数等。根据代价函数以及每次迭代更新的截距与斜率（Θ0，Θ1（一元线性回归只有2个参数）），在最大次数迭代后，画出一条直线，可以看到直线与数据的拟合程度还是比较理想的。

 # 学习率learning rate
 lr = 0.0001
 # 截距
 b = 0
 # 斜率
 k = 0
 # 最大迭代次数（梯度下降法一般都要设置）
 epochs = 50

 # 最小二乘法(代价函数的定义)（用来计算代价函数的值）
 def compute_error(b,k,x_data,y_data):
     # 设置代价函数初始值为0
     totalError = 0
     for i in range(0,len(x_data)):
         totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
     return totalError / float(len(x_data)) / 2.0

 # 用来计算截距和斜率，也就是Θ0，Θ1
 def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
     # 计算机总数据量
     m = float(len(x_data))
     # 循环epochs次
     for i in range(epochs):
         b_grad = 0
         k_grad = 0
         # 计算梯度的总和再求平均
         for j in range(0,len(x_data)):
             b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
             k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
         # 更新b和k
         b = b - (lr * b_grad)
         k = k - (lr * k_grad)
         # 每迭代5次，输出一次图像
         # if i % 5 == 0:
              # print("epochs:",i)
              # plt.plot(x_data,y_data,'b.')
              # plt.plot(x_data, k*x_data+ b,'r')
              # plt.show()
     return b,k
 print("Starting b = {0},k = {1},error = {2}".format(b,k,compute_error(b,k,x_data,y_data)))
 print("Running…")
 b,k = gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
 print("After{0} iteration b = {1},k={2},error = {3}".format(epochs,b,k,compute_error(b,k,x_data,y_data)))

 # 画图,用蓝色的点（b.）画点，用红色画线（r）
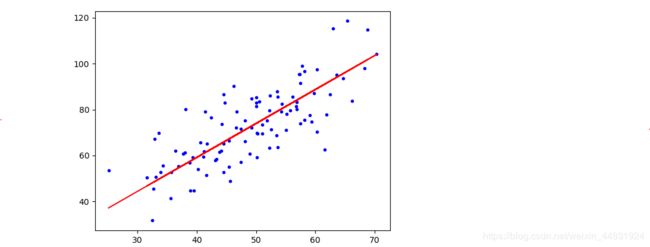
 plt.plot(x_data,y_data,'b.')
 plt.plot(x_data,k*x_data + b,'r')
 plt.show()

最后运行结果和画出的图像如下：
Starting b = 0,k = 0,error = 2782.5539172416056
Running…
After50 iteration b = 0.030569950649287983,k=1.4788903781318357,error = 56.32488184238028

修改上方代码，不是在迭代完成后才画图，而是每迭代5次画一次图，这样把上方代码的注释部分打开，最后一部分的画图代码注释掉，代码如下：

 # 学习率learning rate
 lr = 0.0001
 # 截距
 b = 0
 # 斜率
 k = 0
 # 最大迭代次数（梯度下降法一般都要设置）
 epochs = 50

 # 最小二乘法(代价函数的定义)（用来计算代价函数的值）
 def compute_error(b,k,x_data,y_data):
     # 设置代价函数初始值为0
     totalError = 0
     for i in range(0,len(x_data)):
         totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
     return totalError / float(len(x_data)) / 2.0

 # 用来计算截距和斜率，也就是Θ0，Θ1
 def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
     # 计算机总数据量
     m = float(len(x_data))
     # 循环epochs次
     for i in range(epochs):
         b_grad = 0
         k_grad = 0
         # 计算梯度的总和再求平均
         for j in range(0,len(x_data)):
             b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
             k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
         # 更新b和k
         b = b - (lr * b_grad)
         k = k - (lr * k_grad)
         # 每迭代5次，输出一次图像
         if i % 5 == 0:
               print("epochs:",i)
               plt.plot(x_data,y_data,'b.')
               plt.plot(x_data, k*x_data+ b,'r')
               plt.show()
     return b,k
 print("Starting b = {0},k = {1},error = {2}".format(b,k,compute_error(b,k,x_data,y_data)))
 print("Running…")
 b,k = gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
 print("After{0} iteration b = {1},k={2},error = {3}".format(epochs,b,k,compute_error(b,k,x_data,y_data)))

 # 画图,用蓝色的点（b.）画点，用红色画线（r）
 # plt.plot(x_data,y_data,'b.')
 # plt.plot(x_data,k*x_data + b,'r')
 # plt.show()

这样每迭代5次就会绘制一张图片，总共会绘制出10张图，此处不作粘贴。