完整过程 !!! 的 推荐系统评分预测——SVD与UserCF
注重版权,若要转载烦请附上作者和链接
作者:Joshua_yi
链接:https://blog.csdn.net/weixin_44984664/article/details/106874505
文章目录
- 一、问题描述
- 二、环境介绍
- 三、数据集基础分析
- 四、实验原理
- 1、SVD算法
- 2、UserCF算法
- 五、完成情况
- 六、实现思路及流程
- 1、 数据预处理
- 2、transet和testset划分
- 3、 零模型
- 4、SVD(0-100)
- 5、USER CF(1-5)
- 6、SVD(1-5)
- 7、EDA
- (1)0-100数据的基本分布情况
- (2)1-5的数据分布情况
- (3)矩阵稀疏程度
- 8、 生成预测的分数
- 七、算法实现关键代码
- 1、 较科学的模型评估
- 2、 模型调参过程
- 3、将评分0-100转化为1-5
- 八、实验结果分析
- 九、总结
说明:完整代码与数据集均可在我的github获取
https://github.com/Joshua-li-yi/recommendation_system
此blog仅为菜鸡小编的一次大数据计算与应用课程作业,若有不正确的地方,或有待改进的点,还请大佬们指正
一、问题描述
利用所学算法预测出测试集中每位用户对于给定商品的打分值,并对于预测结果进行误差分析
二、环境介绍
1、 语言:Python
2、 项目管理工具:git
4、Python运行环境:google colab,,surprise,
三、数据集基础分析
1、数据集说明及格式:
train.txt 用于训练模型
|
-
test.txt 用于验证模型
|
-
itemAttribute.txt 用于训练模型(可选)
- |
|('None' means this item is not belong to any of attribute_1/2)
2、数据集统计信息
(1)训练集
用户数量:19835
商品数量:455309
评分数量:5001507
min|max item id:0|6249600
min|max user id:0|19834
min|max rating score: 0|100
(2)测试集
用户数量:19835
min|max item id:34|624958
min|max user id:0|19834
待评价数量:119010
(3)商品集
商品数量:507172
min|max item id: 0|624960
min|max attribute1: 0|624934
min|max attribute2: 0|624951
mean attribute1: 288394.873765
mean attribute2: 272492.800332
std attribute1: 193840.412811
std attribute2: 197227.095516
attribute1 none: 42240
attribute2 none: 63485
商品属性两个都为None的数量:117789
四、实验原理
1、SVD算法
存在一个评分矩阵A,每行代表一个user,每列代表一个item,其中的元素表示user对item的打分,空表示user未对item打分,也就是我们需要预测的值,可以知道,矩阵A是一个极其稀疏的矩阵。 矩阵A可分解为矩阵乘积:
R U × I = P U × K Q K × I R _ { U \times I } = P _ { U \times K } Q _ { K \times I } RU×I=PU×KQK×I
U表示用户数,I表示商品数。然后就是利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分,那么未知的评分也就可以用P的某一行乘上Q的某一列得到了:
r ^ u i = p u T q i \hat { r } _ { u i } = p _ { u } ^ { T } q _ { i } r^ui=puTqi
这是预测用户u对商品i的评分,它等于P矩阵的第u行乘上Q矩阵的第i列。这时需要通过已知评分训练得到P和Q的具体数值,假设已知的评分为: r u i r _ { u i } rui
则真实值与预测值的误差为:
e u i = r u i − r ^ u i e _ { u i } = r _ { u i } - \hat { r } _ { u i } eui=rui−r^ui
继而可以计算出总的误差平方和:
S S E = ∑ u , i e u i 2 = ∑ u , i ( r u i − ∑ k = 1 K p u k q k i ) 2 SSE = \sum _ { u , i } e _ { u i } ^ { 2 } = \sum _ { u , i } ( r _ { u i } - \sum _ { k = 1 } ^ { K } p _ { u k } q _ { k i } ) ^ { 2 } SSE=u,i∑eui2=u,i∑(rui−k=1∑Kpukqki)2
只要通过训练把SSE降到最小,那么P、Q就能最好地拟合R了。 利用梯度下降法可以求得SSE在Puk变量(也就是P矩阵的第u行第k列的值)处的梯度:
∂ ∂ p u k S S E = ∂ ∂ p u k ( e u i 2 ) \frac { \partial } { \partial p _ { u k } } S S E = \frac { \partial } { \partial p _ { u k } } ( e _ { u i } ^ { 2 } ) ∂puk∂SSE=∂puk∂(eui2)
求导后有:
∂ ∂ p u k S S E = ∂ ∂ p u k ( e u i 2 ) = 2 e u i ∂ ∂ p u k e u i = − 2 e u i q k i \frac { \partial } { \partial p _ { u k } } S S E = \frac { \partial } { \partial p _ { u k } } ( e _ { u i } ^ { 2 } ) = 2 e _ { u i } \frac { \partial } { \partial p _ { u k } } e _ { u i } = - 2 e _ { u i } q _ { k i } ∂puk∂SSE=∂puk∂(eui2)=2eui∂puk∂eui=−2euiqki
S S E = 1 2 ∑ u , i e u i 2 = 1 2 ∑ u , i ( r u i − ∑ k = 1 K p u k q k i ) 2 S S E = \frac { 1 } { 2 } \sum _ { u , i } e _ { u i } ^ { 2 } = \frac { 1 } { 2 } \sum _ { u , i } ( r _ { u i } - \sum _ { k = 1 } ^ { K } p _ { u k } q _ { k i } ) ^ { 2 } SSE=21u,i∑eui2=21u,i∑(rui−k=1∑Kpukqki)2
∂ ∂ p u k S S E = − e u i q k i \frac { \partial } { \partial p _ { u k } } S S E = - e _ { u i } q _ { k i } ∂puk∂SSE=−euiqki
现在得到了目标函数在Puk处的梯度了,那么按照梯度下降法,将Puk往负梯度方向变化: 令更新的步长(也就是学习速率)为 η \eta η 则Puk的更新式为
p u k : = p u k − η ( − e u i q k i ) : = p u k + η e u i q k i p _ { u k } : = p _ { u k } - \eta ( - e _ { u i } q _ { k i } ) : = p _ { u k } + \eta e _ { u i } q _ { k i } puk:=puk−η(−euiqki):=puk+ηeuiqki
同样的方式可得到Qik的更新式为
q k i : = q k i − η ( − e u i p u k ) : = q k i + η e u i p u k q _ { k i } : = q _ { k i } - \eta ( - e _ { u i } p _ { u k } ) : = q _ { k i } + \eta e _ { u i } p _ { u k } qki:=qki−η(−euipuk):=qki+ηeuipuk
使用随机梯度下降法,每计算完一个 e u i e _ { u i } eui后立即对pu和qi进行更新。
2、UserCF算法
基于用户的协同过滤算法。
核心思想:
找到和用户A喜好相似的其他用户集合,根据用户集合的打分对预测物品进行打分。
用户相似度:
计算(shrunk)皮尔逊相关系数之间的所有对用户(或项目)使用基线居中,而不是平均值。
shrunk值可以用来帮助降低过拟合
公式如下
p e a r s o n b a s e l i n e s i m ( u , v ) = ρ ^ u v = ∑ i ∈ I u v ( r u i − b u i ) ⋅ ( r v i − b v i ) ∑ i ∈ I u v ( r u i − b u i ) 2 ⋅ ∑ i ∈ I u v ( r v i − b v i ) 2 pearson\;baseline\;sim(u,v)= \hat { \rho } _ { u v } = \frac { \sum _ { i \in I _ { u v } } ( r _ { u i } - b _ { u i } ) \cdot ( r _ { v i } - b _ { v i } ) } { \sqrt { \sum _ { i \in I _ { u v } } ( r _ { u i } - b _ { u i } ) ^ { 2 } } \cdot \sqrt { \sum _ { i \in I _ { u v } } ( r _ { v i } - b _ { v i } ) ^ { 2 } } } pearsonbaselinesim(u,v)=ρ^uv=∑i∈Iuv(rui−bui)2⋅∑i∈Iuv(rvi−bvi)2∑i∈Iuv(rui−bui)⋅(rvi−bvi)
p e a r s o n b a s e l i n e s h r u n k s i m ( u , v ) = ∣ I u v ∣ − 1 ∣ I u v ∣ − 1 + shrinkage ⋅ ρ ^ u v pearson\;baseline\;shrunk\;sim(u,v)= \frac { | I _ { u v } | - 1 } { | I _ { u v } | - 1 + \text { shrinkage } } \cdot \hat { \rho } _ { u v } pearsonbaselineshrunksim(u,v)=∣Iuv∣−1+ shrinkage ∣Iuv∣−1⋅ρ^uv
五、完成情况
1、使用、对比多种模型,0模型、基于用户的协同过滤模型、SVD、,最终选取的模型为SVD,在testset(自己划分)上RMSE分数为13.87345509156839
六、实现思路及流程
1、 数据预处理
将train.txt转为dict类型并保存为pickle文件
格式{use_id:{ item_id: score }}
代码:
import pickle
# 加载train_data 数据类型dict嵌套
# {use_ed:{item_id:score}}
def load_train_data(filepath, output_pickle=False, input_pickle=False):
print('begin load train data')
# 如果选择导入pickle格式的train数据集
if input_pickle is True:
train = pickle.load(open(FILE_PATH + 'train.pickle', 'rb'))
else: # 选择导入 txt格式的训练集
with open(filepath, 'r') as f:
train = {}
while True:
line = f.readline()
if not line or line == '\n':
break
id, item_num = line.split('|')
id = int(id)
item_num = int(item_num)
item = {}
# 遍历之后的内容
for i in range(item_num):
line = f.readline()
item_id, score = line.split(" ")[:2]
# 数据类型转化
score = int(score)
item_id = int(item_id)
# 放入字典中
item[item_id] = score
# 字典嵌套
print(item)
train[id] = item
# print(train)
# 使用dump()将数据序列化到文件中
if output_pickle is True:
with open(FILE_PATH + 'train.pickle', 'wb') as handle:
pickle.dump(train, handle)
print('load train data finish')
return train
2、transet和testset划分
划分方式在train.pickle文件中
从每个用户的评分中随机选取20%的数据,最后整合为一整个testset
而其他的作为trainset
之后的分析和训练过程全部只运用trainset
testset只作为最后的模型评估与评价,因此不会造成数据泄露等问题
最后在预测test.txt文件里的数据的时候,会将trainset和testset作为全部的训练集
从理论上说,在真正test数据集上的分数要比在testset上的评估分数要高一些。
代码
# 随机选择的包
from numpy.random import choice
# 向下取整
from math import floor
import numpy as np
import pandas as pd
import pickle
# 将dict类型的train数据转为df类型,存到trainset.csv 和testset.csv
# test_size = 0.2 选取的测试集的比例
def train_test_divide(train=[], output_csv=False, input_data=False, test_size=0.2):
print('begin divide train and test')
if input_data is True:
# 导入所有的数据集
train = pickle.load(open(FILE_PATH + 'train.pickle', 'rb'))
total_list = []
# 存放test的数据
testset = []
print('begin divide test set')
for id, item in train.items():
# 从一个用户的所用评分中随机选择test_size比例的数据,作为测试集,不重复
test_item_list = choice(list(item.keys()), size=floor(test_size * len(item.keys())), replace=False)
# test
for test_item in test_item_list:
testset.append([id, test_item, item[test_item]])
# 所有的评分
for item_id, score in item.items():
total_list.append([id, item_id, score])
# 将testset有dict转为df类型
test_df = pd.DataFrame(data=testset, columns=['user', 'ID', 'score'])
# 删去testset
del testset
print('begin divide traint set')
# 选区total中有的但是测试集中没有的数据作为训练集
# trainset = [i for i in total_list if i not in testset]
# 将dict类型数据转为df类型
total_df = pd.DataFrame(data=total_list, columns=['user', 'ID', 'score'])
# 删去total list
del total_list
# 先扩展再去重,得到trian
train_df = total_df.append(test_df)
train_df['user'] = train_df['user'].astype(int)
# 所有的train数据减去重复的就是所得剩下的train(此train包含着验证集,也就是说验证集还没有划分)
train_df.drop_duplicates(subset=['user', 'ID', 'score'], keep=False, inplace=True)
if output_csv is True:
print('---------save as csv----------')
total_df.set_index('user', inplace=True)
total_df.to_csv(FILE_PATH + 'train.csv')
del total_df
train_df.set_index('user', inplace=True)
train_df.to_csv(FILE_PATH + 'trainset.csv')
del train_df
test_df.set_index('user', inplace=True)
test_df.to_csv(FILE_PATH + 'testset.csv')
del test_df
print('divide train and test end ')
trainset, testset基本数据分布
trainset
用户数量:19835
商品数量:455309
评分数量:4008915
min|max item id:1|6249600
min|max user id:0|19834
min|max rating score: 0|100
testset
用户数量:19835
商品数量:455309
评分数量:992592
min|max item id:0|6249600
min|max user id:0|19834
min|max rating score: 0|100
3、 零模型
我们选取了trainset中score的均值,50,中位数,众数作为基准,计算了testset中的RMSE值分别为
mean rmse: 38.22805419301362
50 rmse: 38.23329255713531
median rmse: 38.23329255713531
freq rmse: 62.37919526513844
由此看出我们之后选取的模型,最后的RMSE值需要低于38.22805419301362
代码
from sklearn.metrics import mean_squared_error
import pandas as pd
from math import sqrt
# 0模型
def zero_model(testset=[], input_csv=False):
print('zero model begin')
if input_csv is True:
testset = pd.read_csv(FILE_PATH + 'testset.csv')
trainset = pd.read_csv(FILE_PATH + 'trainset.csv')
# 注意直接使用 test_predict1 = testset为浅拷贝
# 使用testset.copy(deep=True) 时为深拷贝
# 使用testset.copy(deep=False) 时为浅拷贝,相当于 test_predict1 = testset
real_score = testset['score']
test_predict = testset.copy(deep=True)
del testset
# 均值
test_predict['pred_mean'] = trainset['score'].mean()
test_predict['pred_50'] = 50
# 中值
test_predict['pred_median'] = trainset['score'].median()
# 众值
test_predict['pred_freq'] = trainset['score'].mode()[0]
# 计算两种的rmse
# zero_model_rmse1 38.223879691036416
# 所得模型的rmse 必须比该值低才有效果
zero_model_rmse1 = sqrt(mean_squared_error(real_score,test_predict['pred_mean']))
# zero_model_rmse2 38.22696157454122
zero_model_rmse2 = sqrt(mean_squared_error(real_score,test_predict['pred_50']))
# 38.23329255713531
zero_model_rmse3 = sqrt(mean_squared_error(real_score,test_predict['pred_median']))
# 62.3791952651384
zero_model_rmse4 = sqrt(mean_squared_error(real_score,test_predict['pred_freq']))
print('mean rmse: ',zero_model_rmse1, '50 rmse: ', zero_model_rmse2, 'median rmse: ', zero_model_rmse3, 'freq rmse: ', zero_model_rmse4)
print('zero model finish')
4、SVD(0-100)
# 基模型
def svd(train=[], input_csv=False, output_csv=False):
print('begin svd')
user_cf_begin = time.perf_counter()
# 告诉文本阅读器,文本的格式是怎么样的
reader = Reader(line_format='user item rating', sep=',', skip_lines=1,rating_scale=(0,100))
# 从csv中加载数据
if input_csv is True:
# 指定文件所在路径
file_path = os.path.expanduser('trainset.csv')
# 加载数据
train_cf = Dataset.load_from_file(file_path, reader=reader)
# 如果训练所有数据取消掉下面的注释
#---------------------------------------------------
trainset = train_cf.build_full_trainset()
#---------------------------------------------------
else:
# 从已有得df中加载数据
train_cf = Dataset.load_from_df(train, reader=reader)
algo = SVD(n_epochs=5, lr_all=0.002, reg_all=0.2, n_factors=650)
print('fit begin')
fit_time_begin = time.perf_counter()
algo.fit(trainset)
fit_time_end = time.perf_counter()
print('fit end')
print('Running time: %s Seconds' % (fit_time_end - fit_time_begin))
user_cf_end = time.perf_counter()
print('Running time: %s Seconds' % (user_cf_end - user_cf_begin))
return algo
algo = svd(trainset_df, input_csv=True, output_csv=False)
test = pd.read_csv('testset.csv')
# 加载真实的score数据
test_score = test['score'].tolist()
# 遍历测试集进行预测
pred =[]
for row in test.itertuples():
# 注意这里一定要 把 user , item_id 转为str格式的
pred.append(algo.predict(str(row[1]), str(row[2]), r_ui=row[3]).est)
del algo
# 四舍五入
pred_round = np.round(pred)
from sklearn.metrics import mean_squared_error
# 计算rmse
rmse = np.sqrt(mean_squared_error(test_score,pred_round))
print('rmse on test scale 0-100:', rmse)
经手动+网格搜索调参后目前为止最好的参数为
n_epochs=5, lr_all=0.002, reg_all=0.2, n_factors=650
运行时间以及RMSE为
Running time: 512.2356659339998 Seconds
rmse on test scale 0-100: 26.8254386470559
5、USER CF(1-5)
尝试了将0-100的scale转换到1-5 , 0-5 ,1-10,0-10多种类别上
发现在1-5上的表现最好
将rating scale转换到1-5上
def scale5(score):
if 0 <= score < 20:
return 1
elif 20 <= score < 40:
return 2
elif 40 <= score < 60:
return 3
elif 60 <= score < 80:
return 4
elif 80 <= score <=100:
return 5
# 基模型
def user_cf(train=[], input_csv=False):
print('begin user cf')
begin = time.perf_counter()
# 告诉文本阅读器,文本的格式是怎么样的
reader = Reader(line_format='user item rating', sep=',', skip_lines=1,rating_scale=(1,5))
# 从csv中加载数据
if input_csv is True:
# 指定文件所在路径
file_path = os.path.expanduser('trainset_score[1,5].csv')
# 加载数据
train_cf = Dataset.load_from_file(file_path, reader=reader)
# 如果训练所有数据取消掉下面的注释
#---------------------------------------------------
trainset = train_cf.build_full_trainset()
#---------------------------------------------------
else:
# 从已有得df中加载数据
train_cf = Dataset.load_from_df(train, reader=reader)
sim_options = {'name': 'pearson_baseline',
'shrinkage': 100 # shrinkage,防止过拟合
}
algo = KNNWithMeans(k=40,sim_options=sim_options) # 1.52
print('fit begin')
fit_time_begin = time.perf_counter()
algo.fit(trainset)
fit_time_end = time.perf_counter()
print('fit end')
print('Running time: %s Seconds' % (fit_time_end - fit_time_begin))
end = time.perf_counter()
print('Running time: %s Seconds' % (end - begin))
return algo
algo = user_cf(input_csv=True)
# 相当于swithch case 语句
def rescale1_5(score):
switcher = {
1: 10,
2: 30,
3: 50,
4: 70,
5: 90,
}
# 默认值为50
return switcher.get(score,50)
total = pd.read_csv('train.csv')
test = pd.read_csv('testset_score[1,5].csv')
# 合并两个df
temp_test = pd.merge(total, test, on=['user','ID'], how='inner')
# print(temp_test.head(10))
del total,test
# 加载真实的score数据
test_score = temp_test['score'].tolist()
# 遍历测试集进行预测
pred =[]
for row in temp_test.itertuples():
# 注意这里一定要 把 user , item_id 转为str格式的
pred.append(algo.predict(str(row[1]), str(row[2]), r_ui=row[4]).est)
# 计算在1-5评分上的rmse
rmse_test = np.sqrt(mean_squared_error(temp_test['score[1,5]'].tolist(),pred))
print('rmse on test scale[1,5]:', rmse_test)
# 四舍五入
pred_round = np.round(pred)
# 从1-5转到原来的数据
pred_score = []
for p in pred_round:
# 先转化为int
pred_score.append(rescale1_5(int(p)))
from sklearn.metrics import mean_squared_error
# 计算rmse
rmse = np.sqrt(mean_squared_error(test_score,pred_score))
print('rmse on test scale 0-100:', rmse)
结果
Running time: 428.300035019 Seconds
rmse on test scale[1,5]: 0.7787991038365966
rmse on test scale 0-100: 19.330745525426316
6、SVD(1-5)
尝试了将0-100的scale转换到1-5 , 0-5 ,1-10,0-10多种类别上
发现在1-5上的表现最好
# 基模型
def svd(train=[], input_csv=False):
print('begin svd')
begin = time.perf_counter()
# 告诉文本阅读器,文本的格式是怎么样的
reader = Reader(line_format='user item rating', sep=',', skip_lines=1,rating_scale=(1,5))
# 从csv中加载数据
if input_csv is True:
# 指定文件所在路径
file_path = os.path.expanduser('trainset_score[1,5].csv')
# 加载数据
train_cf = Dataset.load_from_file(file_path, reader=reader)
# 如果训练所有数据取消掉下面的注释
#---------------------------------------------------
trainset = train_cf.build_full_trainset()
#---------------------------------------------------
else:
# 从已有得df中加载数据
train_cf = Dataset.load_from_df(train, reader=reader)
algo = SVD(n_epochs=350, lr_all=0.003, reg_all=0.01, n_factors=250)
print('fit begin')
fit_time_begin = time.perf_counter()
algo.fit(trainset)
fit_time_end = time.perf_counter()
print('fit end')
print('Running time: %s Seconds' % (fit_time_end - fit_time_begin))
end = time.perf_counter()
print('Running time: %s Seconds' % (end - begin))
return algo
algo = svd(input_csv=True)
# 相当于swithch case 语句
def rescale1_5(score):
switcher = {
1: 10,
2: 30,
3: 50,
4: 70,
5: 90,
}
# 默认值为50
return switcher.get(score,50)
total = pd.read_csv('train.csv')
test = pd.read_csv('testset_score[1,5].csv')
# 合并两个df
temp_test = pd.merge(total, test, on=['user','ID'], how='inner')
# print(temp_test.head(10))
del total,test
# 加载真实的score数据
test_score = temp_test['score'].tolist()
# 遍历测试集进行预测
pred =[]
for row in temp_test.itertuples():
# 注意这里一定要 把 user , item_id 转为str格式的
pred.append(algo2.predict(str(row[1]), str(row[2]), r_ui=row[4]).est)
# 计算在1-5评分上的rmse
rmse_test = np.sqrt(mean_squared_error(temp_test['score[1,5]'].tolist(),pred))
print('rmse on test scale[1,5]:', rmse_test)
# 四舍五入
pred_round = np.round(pred)
# 从1-5转到原来的数据
pred_score = []
for p in pred_round:
# 先转化为int
pred_score.append(rescale1_5(int(p)))
from sklearn.metrics import mean_squared_error
# 计算rmse
rmse = np.sqrt(mean_squared_error(test_score,pred_score))
print('rmse on test scale 0-100:', rmse)
模型结果为
Running time: 8831 Seconds
rmse on test scale[1,5]:0.541747156173787
rmse on test scale0-100:13.87345509156839
7、EDA
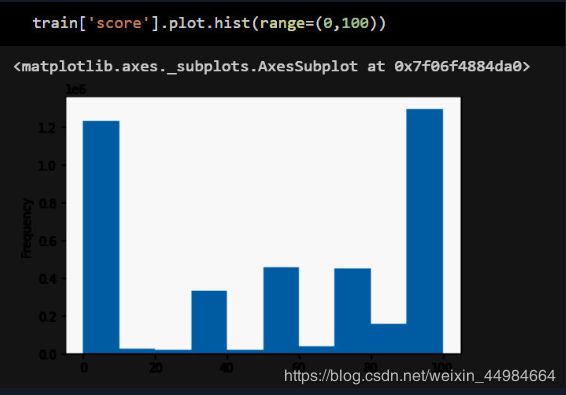
(1)0-100数据的基本分布情况
(2)1-5的数据分布情况
score[1,5]
5 1448238
1 1255993
4 485706
3 473685
2 345293
(3)矩阵稀疏程度
99.9676581902835%
train = pd.read_csv('trainset.csv')
item_max = train['ID'].max()
user_max = train['user'].max()
length = len(train['user'])
# 计算矩阵的稀疏程度
sparsity = 1-length/(item_max*user_max)
8、 生成预测的分数
# 预测test数据,写入结果文件
# 加载test文件
def load_test_data(filepath, output_csv=False):
print('begin load test data ')
# 打开文件
with open(filepath, 'r') as f:
test = []
while True:
line = f.readline()
if not line or line == '\n':
break
id, item_num = line.split('|')
# 类型转化
id = int(id)
item_num = int(item_num)
# 遍历之后的内容
for i in range(item_num):
line = f.readline()
item_id = line
# 数据类型转化
item_id = int(item_id)
# 放入test中
test.append([id, item_id, 0])
# 转为df类型
test = pd.DataFrame(data=test, columns=['user', 'ID', 'score'])
test.set_index('user', inplace=True)
if output_csv is True:
test.to_csv(FILE_PATH+'test.csv')
print('load test data finish')
return test
# 相当于swithch case 语句
def rescale1_5(score):
switcher = {
1: 10,
2: 30,
3: 50,
4: 70,
5: 90,
}
# 默认值为50
return switcher.get(score,50)
test = pd.read_csv('test.csv')
# 遍历测试集进行预测
pred =[]
for row in test.itertuples():
# 注意这里一定要 把 user , item_id 转为str格式的
pred.append(algo2.predict(str(row[1]), str(row[2]), r_ui=row[3]).est)
# 四舍五入
pred_round = np.round(pred)
# 从1-5转到原来的数据
pred_score = []
for p in pred_round:
# 先转化为int
pred_score.append(rescale1_5(int(p)))
test['pred'] = pred_score
test.drop('score', axis=1, inplace=True)
test.set_index('user', inplace=True)
# 保存为csv
test.to_csv('submit.csv')
test = pd.read_csv('submit.csv')
# 写入text
with open("svd.txt","w") as f:
temp_user = 1
for row in test.itertuples():
if temp_user != row[1]:
f.write(str(row[1])+'|6\n')
temp_user = row[1]
f.write(str(row[2])+ " "+ str(row[3])+"\n")
七、算法实现关键代码
1、 较科学的模型评估
trainset 和testset的划分
划分方式在train.pickle文件中
从每个用户的评分中随机选取20%的数据,最后整合为一整个testset
而其他的作为trainset, 之后的分析和训练过程全部只运用trainset,
testset(992592条评分)只作为最后的模型评估与评价,因此不会造成数据泄露等问题
最后在预测test.txt文件里的数据的时候,会将trainset和testset作为全部的训练集,从理论上说,在真正test数据集上的分数要比在testset上的评估分数要高一些。
代码
划分trainset和testset
# 随机选择的包
from numpy.random import choice
# 向下取整
from math import floor
import numpy as np
import pandas as pd
import pickle
# 将dict类型的train数据转为df类型,存到trainset.csv 和testset.csv
# test_size = 0.2 选取的测试集的比例
def train_test_divide(train=[], output_csv=False, input_data=False, test_size=0.2):
print('begin divide train and test')
if input_data is True:
# 导入所有的数据集
train = pickle.load(open(FILE_PATH + 'train.pickle', 'rb'))
total_list = []
# 存放test的数据
testset = []
print('begin divide test set')
for id, item in train.items():
# 从一个用户的所用评分中随机选择test_size比例的数据,作为测试集,不重复
test_item_list = choice(list(item.keys()), size=floor(test_size * len(item.keys())), replace=False)
# test
for test_item in test_item_list:
testset.append([id, test_item, item[test_item]])
# 所有的评分
for item_id, score in item.items():
total_list.append([id, item_id, score])
# 将testset有dict转为df类型
test_df = pd.DataFrame(data=testset, columns=['user', 'ID', 'score'])
# 删去testset
del testset
print('begin divide traint set')
# 选区total中有的但是测试集中没有的数据作为训练集
# trainset = [i for i in total_list if i not in testset]
# 将dict类型数据转为df类型
total_df = pd.DataFrame(data=total_list, columns=['user', 'ID', 'score'])
# 删去total list
del total_list
# 先扩展再去重,得到trian
train_df = total_df.append(test_df)
train_df['user'] = train_df['user'].astype(int)
# 所有的train数据减去重复的就是所得剩下的train(此train包含着验证集,也就是说验证集还没有划分)
train_df.drop_duplicates(subset=['user', 'ID', 'score'], keep=False, inplace=True)
if output_csv is True:
print('---------save as csv----------')
total_df.set_index('user', inplace=True)
total_df.to_csv(FILE_PATH + 'train.csv')
del total_df
train_df.set_index('user', inplace=True)
train_df.to_csv(FILE_PATH + 'trainset.csv')
del train_df
test_df.set_index('user', inplace=True)
test_df.to_csv(FILE_PATH + 'testset.csv')
del test_df
print('divide train and test end ')
2、 模型调参过程
手动调参与网格调参相结合,加快调参速度
param_grid = {'n_factors': [400, 500, 650], 'n_epochs': [30], 'lr_all': [0.006],
'reg_all': [0.01]}
gs = GridSearchCV(SVD, param_grid, measures=['rmse'], cv=3)
gs.fit(train)
# best RMSE score
print(gs.best_score['rmse'])
# combination of parameters that gave the best RMSE score
print(gs.best_params['rmse'])
3、将评分0-100转化为1-5
由推荐系统先验知识可以想到将0-100的scale转换到1-5 , 0-5 ,1-10,0-10多种类别上
经过验证后在1-5,五级评分上模型表现较好
将评分0-100转化为1-5五级评分,提升了模型的精度,最后将1-5再转化为0-100,不影响最后的结果
也是该模型RMSE降到20以下的一个关键点
# 相当于swithch case 语句
def rescale1_5(score):
switcher = {
1: 10,
2: 30,
3: 50,
4: 70,
5: 90,
}
# 默认值为50
return switcher.get(score,50)
八、实验结果分析
1、
| model | RMSE(0-100) | Time(s) |
|---|---|---|
| 0 model | 38.22805419301362 | – |
| SVD(0-100) | 26.8254386470559 | 512.2356659339998 |
| user cf(1-5) | 19.330745525426316 | 428.300035019 |
| SVD(1-5) | 13.87345509156839 | 8831.020578701 |
2、训练集数据本身结构(如0分过多)、矩阵过于稀疏(稀疏率99.9676581902835%)对降低RMSE带来一定的困难
九、总结
以上是小编使用SVD与USER CF算法进行评分预测的一个总结,如果哪个地方有误,欢迎指正,也同时欢迎大佬们在评论区分享补充~~
如果觉得本文对你们有帮助的话,请给小编来个小心心,评论与关注 三连吧~~,让更多的童鞋可以看到
有兴趣的小伙伴,也可以使用小编最后训练完的模型,由于模型较大(1.03GB),给出百度网盘链接,欢迎使用~~
链接:https://pan.baidu.com/s/1y1vzf9RJOM0xMre5ZXy_pQ
提取码:5xq3
完整代码与数据集均可在我的github获取
https://github.com/Joshua-li-yi/recommendation_system